Support Vector Machine o SVM è uno dei più popolari algoritmi di apprendimento supervisionato, che viene utilizzato per la classificazione e problemi di regressione. Tuttavia, principalmente, viene utilizzato per problemi di classificazione nell’apprendimento automatico.
L’obiettivo dell’algoritmo SVM è quello di creare la linea migliore o il limite decisionale che può separare lo spazio n-dimensionale in classi in modo da poter facilmente inserire il nuovo punto dati nella categoria corretta in futuro., Questo limite di decisione migliore è chiamato un iperpiano.
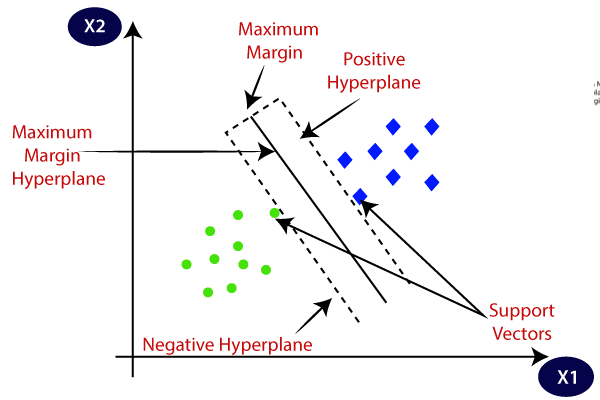
SVM sceglie i punti/vettori estremi che aiutano a creare l’iperpiano. Questi casi estremi sono chiamati come vettori di supporto, e quindi l’algoritmo è definito come Macchina vettoriale di supporto. Considera il diagramma seguente in cui ci sono due diverse categorie che sono classificate usando un limite di decisione o un iperpiano:
Esempio: SVM può essere compreso con l’esempio che abbiamo usato nel classificatore KNN., Supponiamo di vedere uno strano gatto che ha anche alcune caratteristiche dei cani, quindi se vogliamo un modello in grado di identificare con precisione se si tratta di un gatto o di un cane, quindi un tale modello può essere creato utilizzando l’algoritmo SVM. Per prima cosa addestreremo il nostro modello con molte immagini di cani e gatti in modo che possa conoscere le diverse caratteristiche di cani e gatti, e poi lo testeremo con questa strana creatura. Quindi, poiché il vettore di supporto crea un confine decisionale tra questi due dati (gatto e cane) e sceglie casi estremi (vettori di supporto), vedrà il caso estremo di gatto e cane., Sulla base dei vettori di supporto, lo classificherà come un gatto. Si consideri lo schema seguente:
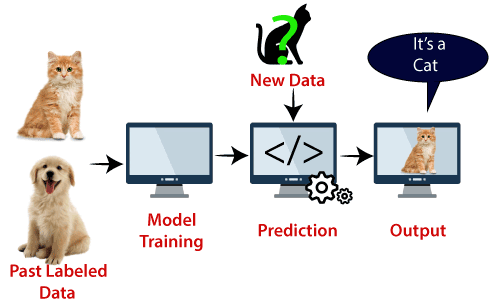
L’algoritmo SVM può essere utilizzato per il rilevamento dei volti, la classificazione delle immagini, la categorizzazione del testo, ecc.
Tipi di SVM
SVM possono essere di due tipi:
- SVM lineare: SVM lineare viene utilizzato per i dati separabili linearmente, il che significa che se un set di dati può essere classificato in due classi utilizzando una singola linea retta, allora tali dati vengono definiti come dati separabili linearmente, e classificatore viene utilizzato,
- SVM non lineare: SVM non lineare viene utilizzato per dati non linearmente separati, il che significa che se un set di dati non può essere classificato utilizzando una linea retta, tali dati vengono definiti come dati non lineari e il classificatore utilizzato viene chiamato classificatore SVM non lineare.
Hyperplane e vettori di supporto nell’algoritmo SVM:
Hyperplane: ci possono essere più linee / limiti decisionali per separare le classi nello spazio n-dimensionale, ma abbiamo bisogno di scoprire il miglior limite decisionale che aiuta a classificare i punti dati. Questo limite migliore è noto come iperpiano di SVM.,
Le dimensioni dell’iperpiano dipendono dalle caratteristiche presenti nel set di dati, il che significa che se ci sono 2 caratteristiche (come mostrato nell’immagine), allora l’iperpiano sarà una linea retta. E se ci sono 3 caratteristiche, allora hyperplane sarà un piano a 2 dimensioni.
Creiamo sempre un iperpiano che ha un margine massimo, che significa la distanza massima tra i punti dati.
Vettori di supporto:
I punti dati o vettori che sono i più vicini all’iperpiano e che influenzano la posizione dell’iperpiano sono definiti come Vettore di supporto., Poiché questi vettori supportano l’iperpiano, quindi chiamato vettore di supporto.
Come funziona SVM?
SVM lineare:
Il funzionamento dell’algoritmo SVM può essere compreso usando un esempio. Supponiamo di avere un set di dati con due tag (verde e blu) e il set di dati ha due funzionalità x1 e x2. Vogliamo un classificatore in grado di classificare la coppia(x1, x2) di coordinate in verde o blu. Considera l’immagine qui sotto:
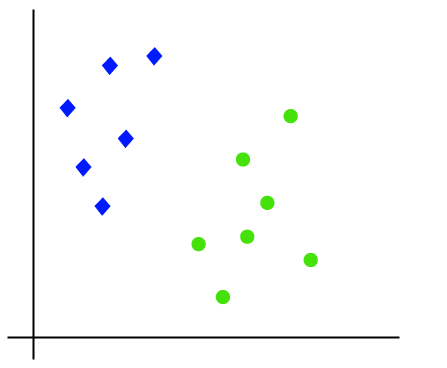
Così come è lo spazio 2-d quindi usando solo una linea retta, possiamo facilmente separare queste due classi., Ma ci possono essere più righe che possono separare queste classi. Considera l’immagine qui sotto:
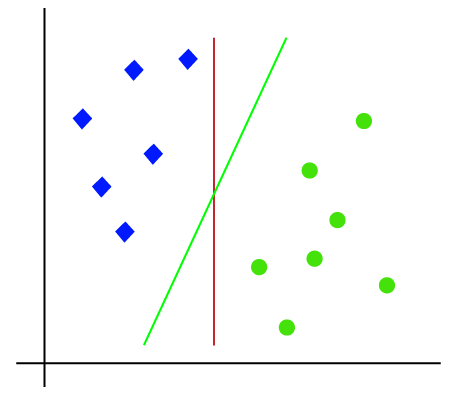
Quindi, l’algoritmo SVM aiuta a trovare la linea migliore o il limite di decisione; questo limite o regione migliore è chiamato come un iperpiano. L’algoritmo SVM trova il punto più vicino delle linee da entrambe le classi. Questi punti sono chiamati vettori di supporto. La distanza tra i vettori e l’iperpiano è chiamata margine. E l’obiettivo di SVM è massimizzare questo margine. L’iperpiano con margine massimo è chiamato iperpiano ottimale.,
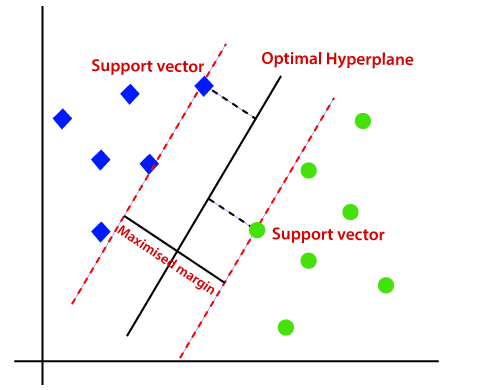
SVM non lineare:
Se i dati sono disposti linearmente, possiamo separarli usando una linea retta, ma per i dati non lineari, non possiamo disegnare una singola linea retta. Considera l’immagine qui sotto:
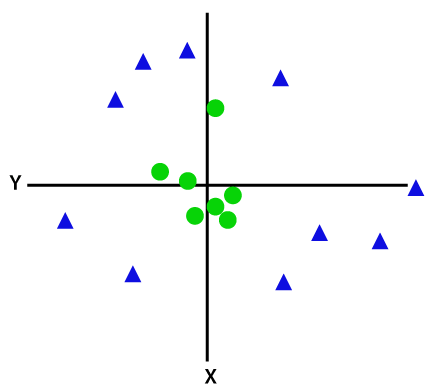
Quindi per separare questi punti dati, dobbiamo aggiungere un’altra dimensione. Per i dati lineari, abbiamo usato due dimensioni x e y, quindi per i dati non lineari, aggiungeremo una terza dimensione z., Può essere calcolato come:
z=x2 +y2
Aggiungendo la terza dimensione, lo spazio campione diventerà come sotto immagine:
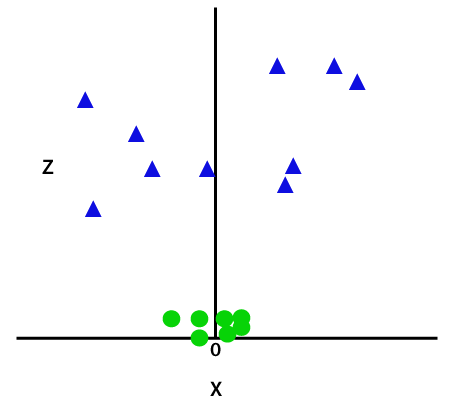
Così ora, SVM dividerà i set di dati in classi nel modo seguente. Considera l’immagine qui sotto:
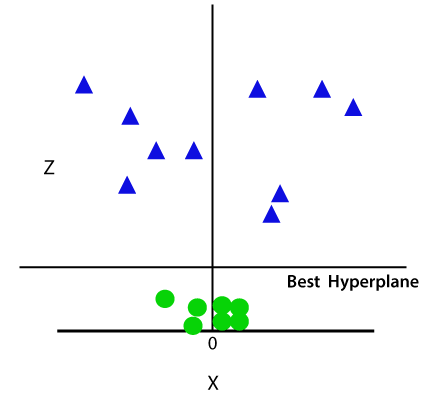
Poiché siamo nello spazio 3D, quindi sembra un piano parallelo all’asse x. Se lo convertiamo in spazio 2d con z = 1, allora diventerà come:
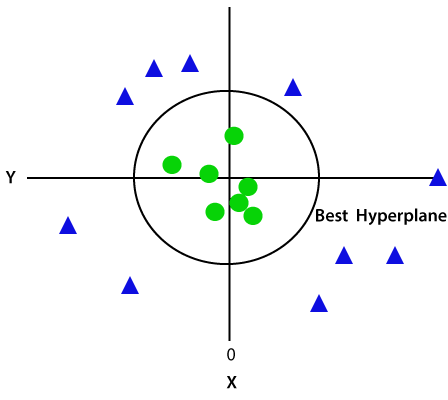
Quindi otteniamo una circonferenza di raggio 1 in caso di dati non lineari.,
Implementazione Python della macchina vettoriale di supporto
Ora implementeremo l’algoritmo SVM usando Python. Qui useremo lo stesso set di dati user_data, che abbiamo usato nella regressione logistica e nella classificazione KNN.
- Fase di pre-elaborazione dei dati
Fino alla fase di pre-elaborazione dei dati, il codice rimarrà lo stesso. Di seguito è riportato il codice:
Dopo aver eseguito il codice di cui sopra, pre-elaborare i dati., Il codice darà il set di dati come:
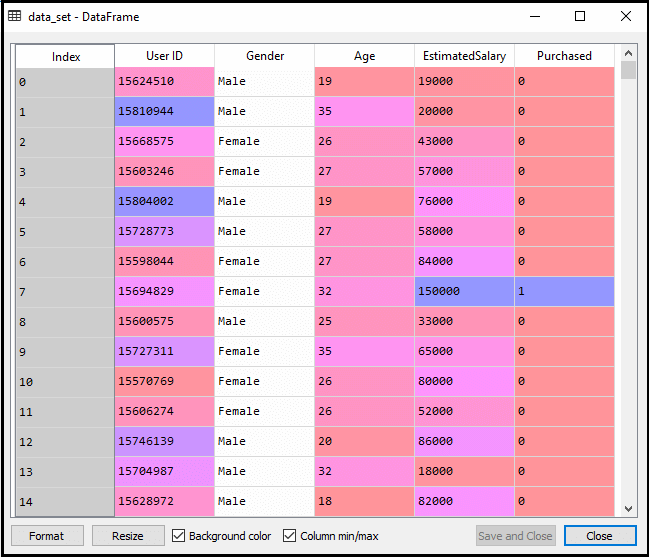
L’output scalato per il set di test sarà:
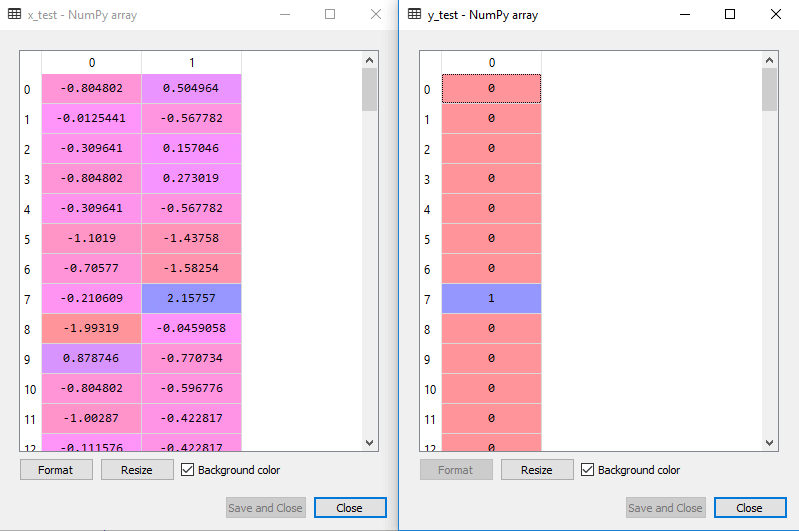
Montaggio del classificatore SVM al set di allenamento:
Ora il set di allenamento sarà montato sul classificatore SVM. Per creare il classificatore SVM, importeremo la classe SVC da Sklearn.libreria svm. Di seguito è riportato il codice per esso:
Nel codice sopra, abbiamo usato kernel=’linear’, poiché qui stiamo creando SVM per dati separabili linearmente. Tuttavia, possiamo cambiarlo per dati non lineari., E poi abbiamo montato il classificatore sul set di dati di allenamento(x_train, y_train)
Output:
Le prestazioni del modello possono essere modificate modificando il valore di C (fattore di regolarizzazione), gamma e kernel.
- Previsione del risultato del set di test:
Ora, prevederemo l’output per il set di test. Per questo, creeremo un nuovo vettore y_pred. Di seguito è riportato il codice per esso:
Dopo aver ottenuto il vettore y_pred, possiamo confrontare il risultato di y_pred e y_test per verificare la differenza tra il valore effettivo e il valore previsto.,
Output: Di seguito è riportato l’output per la previsione del set di test:

- Creazione della matrice di confusione:
Ora vedremo le prestazioni del classificatore SVM che quante previsioni errate ci sono rispetto al classificatore di regressione logistica. Per creare la matrice di confusione, dobbiamo importare la funzione confusion_matrix della libreria sklearn. Dopo aver importato la funzione, la chiameremo usando una nuova variabile cm. La funzione prende due parametri, principalmente y_true (i valori effettivi) e y_pred (il valore mirato restituito dal classificatore)., Di seguito è riportato il codice per esso:
Output:
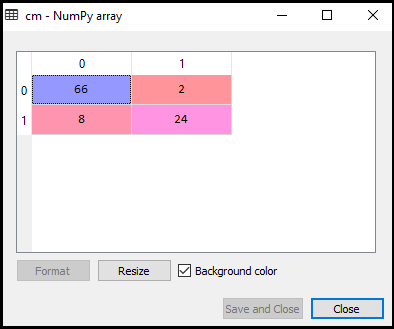
Come possiamo vedere nell’immagine di output sopra, ci sono 66+24= 90 previsioni corrette e 8+2= 10 previsioni corrette. Quindi possiamo dire che il nostro modello SVM è migliorato rispetto al modello di regressione logistica.,
- Visualizzare il set di training risultato:
Ora possiamo visualizzare il set di training risultato, al di sotto è il codice:
Uscita:
eseguendo il codice di cui sopra, vi saranno mostrati anche l’output come:
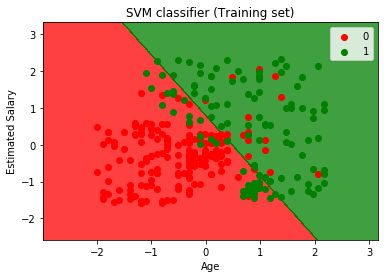
Come si può vedere, output sopra appare simile alla regressione Logistica in uscita. Nell’output, abbiamo ottenuto la linea retta come hyperplane perché abbiamo usato un kernel lineare nel classificatore. E abbiamo anche discusso sopra che per lo spazio 2d, l’iperpiano in SVM è una linea retta.,
- Visualizzazione del risultato del set di test:
Output:
Eseguendo il codice di cui sopra, otterremo l’output come:
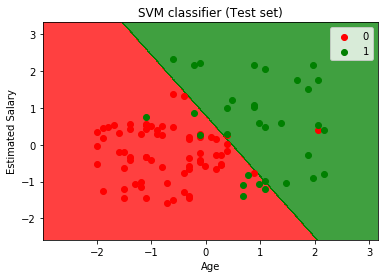
Come possiamo vedere nell’immagine di output sopra, il classificatore SVM ha diviso gli utenti in due regioni (acquistate o non acquistate). Gli utenti che hanno acquistato il SUV si trovano nella regione rossa con i punti scatter rossi. E gli utenti che non hanno acquistato il SUV sono nella regione verde con punti scatter verdi. L’iperpiano ha diviso le due classi in variabile acquistata e non acquistata.