Questa è la prima di una serie di tre post. Il secondo post parla di come calcolare Big-O. Il terzo articolo parla della comprensione della definizione formale di Big-O.
La notazione Big-O era un concetto davvero spaventoso per me. Ho pensatoquesto è il modo in cui i programmatori “reali” hanno parlato del loro codice. Era tutto più spaventoso perché le descrizioni accademiche (come Wikipedia) avevano molto poco senso per me. Questo è frustrante perché i concetti sottostanti non sono in realtà così difficili.,
In poche parole, la notazione Big-O è il modo in cui i programmatori parlano dialgoritmi. Gli algoritmi sono un altro argomento spaventoso che tratterò in un altro post, ma per i nostri scopi, diciamo che “algoritmo” significa una funzione nel tuo programma (che non è troppo lontano). La Grande onotazione di una funzione è determinata dal modo in cui risponde a diversi input. Howmuch più lento è se gli diamo una lista di 1000 cose su cui lavorare, invece di una lista di 1 cosa?
Considera questo codice:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Quindi se chiamiamo questa funzione come item_in_list(2, ), dovrebbe essere piuttosto veloce., Eseguiamo il loop su ogni cosa nella lista e se troviamoil primo argomento della nostra funzione, restituisce True. Se arriviamo alla finee non l’abbiamo trovato, restituisci Falso.
La “complessità” di questa funzione èO(n). Spiegherò cosa significa in un secondo, ma analizziamo questa sintassi matematica. O(n)viene letto” Ordine di N”perché la funzioneO è anche nota come funzione di ordine. Penso che questo sia perché stiamo facendo l’approssimazione, che si occupa di “ordini di grandezza”.,
“Ordini di grandezza” è ANCORA UN ALTRO termine matematico whichbasically dice la differenza tra le classi di numeri. Pensate thedifference tra 10 e 100. Se immagini 10 dei tuoi closestfriends e 100 persone, questa è davvero una grande differenza. Allo stesso modo, la differenza tra 1.000 e 10.000 è piuttosto grande (in effetti, è la differenza tra un’auto junker e una leggermente usata). Si scopre che in approssimazione, finché sei all’interno di un ordine di grandezza,sei abbastanza vicino., Se dovessi indovinare il numero di gumballs in amachine, saresti all’interno di un ordine di grandezza se dicessi 200gumballs. 10.000 gumballs sarebbero fuori strada.

Figura 1: Un gumball machine il cui numero di gumballs è probabilmente all’interno di un ordine di grandezza di 200.
Torna a sezionare O(n), questo dice che se dovessimo rappresentare graficamente il tempo necessario per eseguire questa funzione con input di dimensioni diverse (ad esempio un raggio di 1 elemento, 2 elementi, 3 elementi, ecc.), vedremmo che corrisponde approssimativamente al numero di elementi nell’array., Questo isalled un grafico lineare. Ciò significa che la linea è fondamentalmente straightif si dovesse graficamente.
Alcuni di voi potrebbero aver scoperto che se, nell’esempio di codice sopra, il nostro oggetto fosse sempre il primo elemento della lista, il nostro codice sarebbe davvero veloce! Questo è vero, ma Big-O riguarda l’approssimativo caso peggiore di fare qualcosa. Il caso peggiore per il codice sopra èche la cosa che stiamo cercando non è affatto nella lista. (Nota: il termine matematico per questo è “upper bound”, il che significa che parla del limite matematico di awfulness).,
Se si desidera visualizzare un grafico per queste funzioni, si ignora la funzione O()e si modifica la variabile n per x. Puoi quindi digitare thatinto Wolfram Alpha come “plot x” che ti mostrerà una diagonallina. Il motivo per cui si scambia n per x è che il loro programma di graficavuole x come nome della variabile perché corrisponde allo xaxis. L’asse x che diventa più grande da sinistra a destra corrisponde a dare array sempre più grandi alla tua funzione., L’asse y rappresenta il tempo, quindi più alta è la linea, più lenta è.
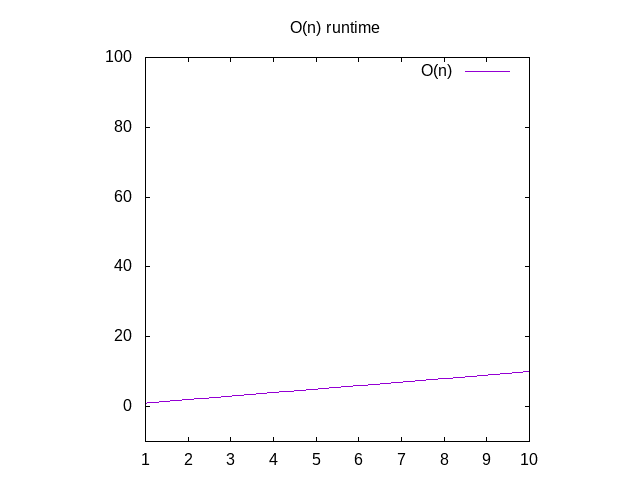
Figura 2: Caratteristiche di runtime di una funzione O(n)
Quindi quali sono alcuni altri esempi di questo?
Considera questa funzione:
def is_none(item): return item is None
Questo è un esempio un po ‘ stupido, ma porta con me. Questa funzione è chiamata O(1) che si chiama”tempo costante”. Ciò significa che non importa quanto sia grande il nostro input, ci vuole sempre la stessa quantità di tempo per calcolare le cose., Se torni a Wolfram eplot 1, vedrai che rimane sempre lo stesso, non importa quanto a destra andiamo. Se youpass in un elenco di 1 milione di interi, ci vorrà circa lo stesso tempocome se si dovesse passare in un elenco di 1 intero. Il tempo costante è considerato lo scenario migliore per una funzione.
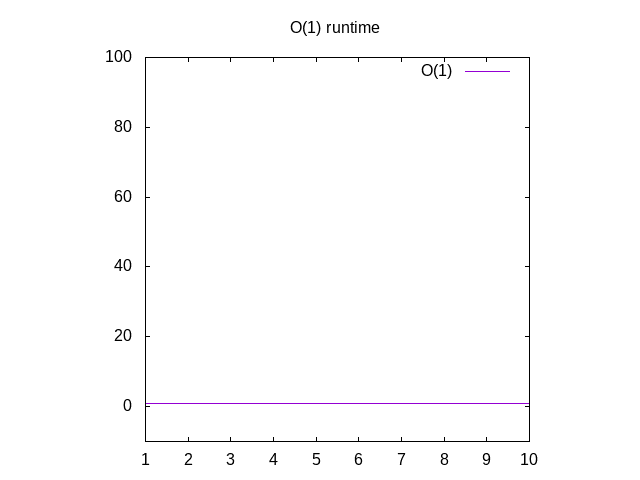
Figura 3: Caratteristiche di runtime di una funzione O(1)
Considera questa funzione:
Di seguito è riportato un confronto di ciascuno di questi grafici, come riferimento., Puoi vedere che una funzioneO(n^2) diventerà lenta molto rapidamente dove qualcosa che funziona in tempo costante sarà molto meglio. Ciò è particolarmente utile quando si tratta di strutture dati, che pubblicherò presto.
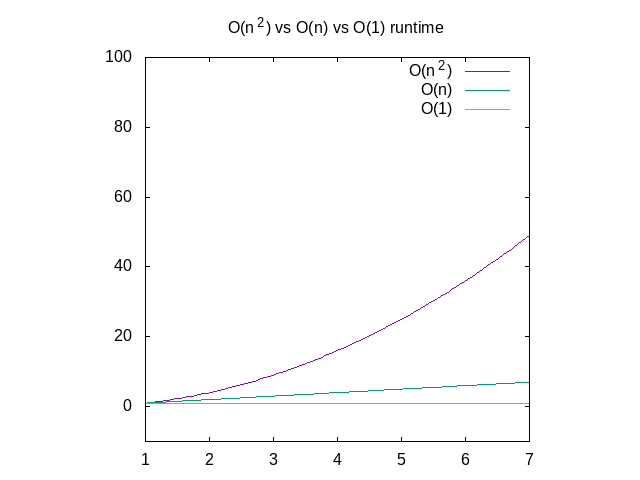
Figura 4: Confronto delle funzioni O(n2) vs O(n) vs O(1)
Questa è una panoramica di livello piuttosto alto della notazione Big-O, ma hopefullygets conosci l’argomento., C’è un corso di coursera che può darti una visione più approfondita di questo argomento, ma sii avvertito che salterà in notazione matematica molto rapidamente. Se qualcosa qui non ha senso, mandami una e-mail.
Aggiornamento: Ho anche scritto su come calcolare Big-O.
Sto pensando di scrivere un libro su questo argomento. Se questo è qualcosa che vorresti vedere, per favore esprimi il tuo interesse qui.