Varianza misura quanto un set di dati è steso. Una varianza pari a zero indica che tutti i valori dei dati sono identici. Tutte le varianze diverse da zero sono positive.

Una piccola varianza indica che i punti dati tendono ad essere molto vicini alla media e tra loro., Un’alta varianza indica che i punti dati sono molto distribuiti dalla media e l’uno dall’altro. La varianza è la media delle distanze quadrate da ciascun punto alla media.

Il processo di ricerca della varianza è molto simile a trovare la deviazione assoluta MAD, media.
L’unica differenza è la quadratura delle distanze.
Processo: (1) Trova la media (media) del set. (2) Sottrarre ogni valore di dati dalla media per trovare la sua distanza dalla media. (3) Piazza tutte le distanze. (4) Aggiungere tutti i quadrati delle distanze., (4) Dividere per il numero di pezzi di dati (per la varianza della popolazione).

Un problema con la varianza è che non ha la stessa unità di misura dei dati originali. Ad esempio, i dati originali contenenti lunghezze misurate in piedi hanno una varianza misurata in piedi quadrati.,

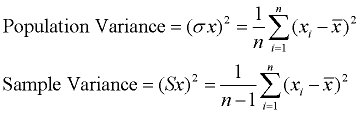Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Se si calcola a mano, portare sempre più cifre decimali all’interno dei calcoli di quanto previsto per il risultato finale. Se si lavora con una calcolatrice, portare l’intero valore delle voci calcolatrice fino ad arrivare al risultato finale.

deviazione Standard indica la variabilità (dispersione, diffusione, dispersione dalla media esiste., Rappresenta una deviazione “tipica” dalla media. È una misura popolare di variabilità perché ritorna alle unità di misura originali del set di dati.

Una bassa deviazione standard indica che i punti dati tendono ad essere molto vicini alla media. Una deviazione standard elevata indica che i punti dati sono distribuiti su un ampio intervallo di valori.
La deviazione standard può essere pensata come un modo “standard” per conoscere ciò che è normale (tipico), ciò che è molto grande e ciò che è molto piccolo nel set di dati.,

La deviazione standard è una misura popolare di variabilità perché ritorna alle unità di misura originali del set di dati. Ad esempio, i dati originali contenenti lunghezze misurate in piedi hanno una deviazione standard misurata anche in piedi.,

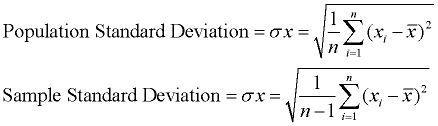Per calcolare la deviazione standard con la mano:
La deviazione standard è semplicemente la radice quadrata della varianza.
Questa descrizione è per calcolare la deviazione standard della popolazione. Se è necessaria una deviazione standard del campione, dividere per n-1 invece di n., Poiché la deviazione standard è la radice quadrata della varianza, dobbiamo prima calcolare la varianza.
1. Trova la media.
2. Sottrai la media da ciascun valore di dati e piazza ciascuna di queste differenze (le differenze al quadrato).
3. Trova la media delle differenze al quadrato (aggiungile e dividi per il conteggio dei valori dei dati). Questa sarà la varianza.,

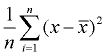varianza
4. Prendi la radice quadrata. Questa sarà la deviazione standard della popolazione. Arrotondare la risposta in base alle indicazioni del problema.

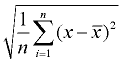deviazione standard

Curva normale

Una curva normale è simmetrica, curva a forma di campana., Il centro del grafico è la media e l’altezza e la larghezza del grafico sono determinate dalla deviazione standard. Quando la deviazione standard è piccola, la curva sarà alta e stretta nella diffusione. Quando la deviazione standard è grande, la curva sarà breve e larga in diffusione. La media e la mediana hanno lo stesso valore in una curva normale.

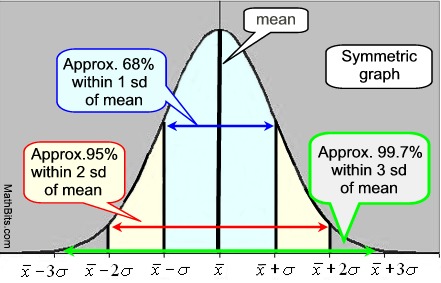
Curva normale Regola empirica:
Circa …

• Il 68% dei dati rientra in una deviazione standard della media.,

• Il 95% dei dati si trova entro due deviazioni standard della media.

• Il 99,7% dei dati si trova entro tre deviazioni standard della media.

IQR per una curva normale è 1.34896 x deviazione standard.