Noi classicamente pensiamo alla luce come sempre viaggiando in linee rette, ma quando le onde luminose passano vicino a una barriera tendono a piegarsi attorno a quella barriera e si diffondono. La diffrazione della luce si verifica quando un’onda luminosa passa da un angolo o attraverso un’apertura o una fessura che è fisicamente la dimensione approssimativa di, o anche più piccola della lunghezza d’onda di quella luce.,

Una dimostrazione molto semplice della diffrazione può essere condotta tenendo la mano davanti a una sorgente luminosa e chiudendo lentamente due dita osservando la luce trasmessa tra di loro. Mentre le dita si avvicinano l’una all’altra e si avvicinano molto, si inizia a vedere una serie di linee scure parallele alle dita. Le linee parallele sono in realtà modelli di diffrazione. Questo fenomeno può verificarsi anche quando la luce è “piegata” attorno a particelle che si trovano sullo stesso ordine di grandezza della lunghezza d’onda della luce., Un buon esempio di questo è la diffrazione della luce solare da parte delle nuvole che spesso ci riferiamo a come un rivestimento d’argento, illustrato in Figura 1 con un bellissimo tramonto sull’oceano.
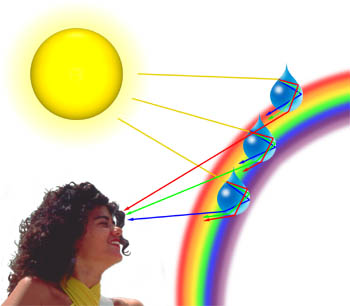
Spesso possiamo osservare sfumature pastello di blu, rosa, viola e verde nelle nuvole che vengono generate quando la luce viene diffratta dalle gocce d’acqua nelle nuvole. La quantità di diffrazione dipende dalla lunghezza d’onda della luce, con lunghezze d’onda più corte che sono diffratte ad un angolo maggiore di quelle più lunghe (in effetti, la luce blu e viola sono diffratte ad un angolo superiore a quello della luce rossa)., Come un’onda luminosa che viaggia attraverso l’atmosfera incontra una goccia d’acqua, come illustrato di seguito, viene prima rifratta all’interfaccia acqua:aria, quindi viene riflessa mentre incontra nuovamente l’interfaccia. Il raggio, ancora in viaggio all’interno della goccia d’acqua, viene nuovamente rifratto mentre colpisce l’interfaccia per la terza volta. Quest’ultima interazione con l’interfaccia rifrange la luce nell’atmosfera, ma diffratta anche una parte della luce come illustrato di seguito., Questo elemento di diffrazione porta ad un fenomeno noto come alone di Cellini (noto anche come effetto Heiligenschein) dove un anello luminoso di luce circonda l’ombra della testa dell’osservatore.
I termini diffrazione e scattering sono spesso usati in modo intercambiabile e sono considerati quasi sinonimi. La diffrazione descrive un caso specializzato di dispersione della luce in cui un oggetto con caratteristiche che si ripetono regolarmente (come una griglia di diffrazione) produce una diffrazione ordinata della luce in un modello di diffrazione., Nel mondo reale la maggior parte degli oggetti ha una forma molto complessa e dovrebbe essere considerata composta da molte caratteristiche di diffrazione individuali che possono produrre collettivamente una dispersione casuale di luce.
Uno dei concetti classici e più fondamentali che coinvolgono la diffrazione è l’esperimento di diffrazione ottica a fessura singola, condotto per la prima volta all’inizio del XIX secolo. Quando un’onda luminosa si propaga attraverso una fessura (o apertura) il risultato dipende dalla dimensione fisica dell’apertura rispetto alla lunghezza d’onda del fascio incidente., Questo è illustrato nella Figura 3, supponendo una coerente, monocromatica onda emessa dalla sorgente puntiforme S, simile alla luce prodotta da un laser, passa attraverso il diaframma d e viene diffratta, con il primario del fascio di luce incidente in atterraggio al punto P e il primo secondaria maxima che si verificano al punto D.
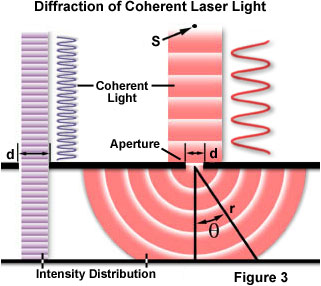
Come mostrato nella parte sinistra della figura, quando la lunghezza d’onda (λ) è molto più piccolo del diaframma larghezza (d), l’onda viaggia semplicemente in avanti in linea retta, come se si trattasse di una particella o di apertura erano presenti., Tuttavia, quando la lunghezza d’onda supera la dimensione dell’apertura, sperimentiamo la diffrazione della luce secondo l’equazione:
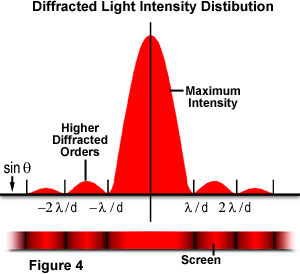
Dove θ è l’angolo tra la direzione di propagazione centrale incidente e il primo minimo del modello di diffrazione. L’esperimento produce un massimo centrale luminoso che è affiancato su entrambi i lati da massimi secondari, con l’intensità di ogni massimo secondario successivo che diminuisce all’aumentare della distanza dal centro. La figura 4 illustra questo punto con un grafico dell’intensità del fascio rispetto al raggio di diffrazione., Si noti che i minimi che si verificano tra massimi secondari si trovano in multipli di π.
Questo esperimento è stato spiegato per la prima volta da Augustin Fresnel che, insieme a Thomas Young, ha prodotto importanti prove che confermano che la luce viaggia in onde. Dalle figure sopra, vediamo come una luce coerente e monocromatica (in questo esempio, l’illuminazione laser) emessa dal punto L è diffratta dall’apertura d., Fresnel assunto che l’ampiezza del primo ordine massimi di cui al punto Q (definito come eQ) sarebbe dato dall’equazione:
dove A è l’ampiezza dell’onda incidente, r è la distanza tra d e D e f(x) è una funzione di x, un’inclinazione fattore introdotto da Fresnel.
Diffrazione della luce
Esplora come un fascio di luce viene diffratto quando passa attraverso una stretta fessura o apertura. Regolare la lunghezza d’onda e la dimensione dell’apertura e osservare come questo influenza il modello di intensità di diffrazione.,
La diffrazione della luce gioca un ruolo fondamentale nel limitare il potere risolutivo di qualsiasi strumento ottico (ad esempio: macchine fotografiche, binocoli, telescopi, microscopi e l’occhio). Il potere risolutivo è la capacità dello strumento ottico di produrre immagini separate di due punti adiacenti. Questo è spesso determinato dalla qualità delle lenti e degli specchi nello strumento, nonché dalle proprietà del mezzo circostante (di solito aria). La natura ondulatoria della luce impone un limite massimo al potere risolutivo di tutti gli strumenti ottici.,
Le nostre discussioni sulla diffrazione hanno usato una fessura come apertura attraverso la quale la luce viene diffratta. Tuttavia, tutti gli strumenti ottici hanno aperture circolari, ad esempio la pupilla di un occhio o il diaframma circolare e le lenti di un microscopio. Aperture circolari producono modelli di diffrazione simili a quelli descritti sopra, tranne il modello presenta naturalmente una simmetria circolare. L’analisi matematica dei pattern di diffrazione prodotti da un’apertura circolare è descritta dall’equazione:
dove θ (1) è la posizione angolare dei minimi di diffrazione del primo ordine (il primo anello scuro), λ è la lunghezza d’onda della luce incidente, d è il diametro dell’apertura e 1.22 è una costante. Nella maggior parte dei casi, l’angolo θ(1) è molto piccola, quindi l’approssimazione che il peccato e l’abbronzatura dell’angolo sono quasi uguali rendimenti:
Da queste equazioni diventa evidente che il centro di massima è direttamente proporzionale a λ/d questa massima più diffuso per lunghezze d’onda più lunghe e per diaframmi più chiusi., La mimina secondaria della diffrazione ha fissato un limite all’ingrandimento utile delle lenti dell’obiettivo nella microscopia ottica, dovuto la diffrazione inerente di luce da queste lenti. Non importa quanto sia perfetta la lente, l’immagine di una fonte puntiforme di luce prodotta dalla lente è accompagnata da massimi di ordine secondario e superiore. Questo potrebbe essere eliminato solo se la lente avesse un diametro infinito. Due oggetti separati da una distanza inferiore a θ(1) non possono essere risolti, non importa quanto sia alta la potenza di ingrandimento., Mentre queste equazioni sono state derivate per l’immagine di una sorgente puntiforme di luce una distanza infinita dall’apertura, è una ragionevole approssimazione del potere risolutivo di un microscopio quando d è sostituito per il diametro della lente obiettivo.
Quindi, se due oggetti risiedono a una distanza D l’uno dall’altro e si trovano a una distanza L da un osservatore, l’angolo (espresso in radianti) tra di loro è:
che ci porta ad essere in grado di condensare le ultime due equazioni per produrre:
Dove D (0) è la distanza minima di separazione tra gli oggetti che consentirà loro di essere risolti. Usando questa equazione, l’occhio umano può risolvere oggetti separati da una distanza di 0,056 millimetri, tuttavia i fotorecettori nella retina non sono abbastanza vicini insieme per consentire questo grado di risoluzione, e 0,1 millimetri è un numero più realistico in circostanze normali.
Il potere risolutivo dei microscopi ottici è determinato da una serie di fattori tra cui quelli discussi, ma nelle circostanze più ideali, questo numero è di circa 0,2 micrometri., Questo numero deve tenere conto dell’allineamento ottico del microscopio, della qualità delle lenti e delle lunghezze d’onda predominanti della luce utilizzate per l’immagine del campione. Mentre spesso non è necessario calcolare l’esatto potere risolutivo di ciascun obiettivo (e sarebbe una perdita di tempo nella maggior parte dei casi), è importante capire le capacità delle lenti del microscopio come si applicano al mondo reale.
Autori
Mortimer Abramowitz-Olympus America, Inc., Due unità Centro aziendale., Melville, New York, 11747.
Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., La Florida State University, Tallahassee, Florida, 32310.