Introduzione
La regressione lineare, nota anche come regressione lineare semplice o regressione lineare bivariata, viene utilizzata quando si desidera prevedere il valore di una variabile dipendente in base al valore di una variabile indipendente. Ad esempio, è possibile utilizzare la regressione lineare per capire se le prestazioni dell’esame possono essere previste in base al tempo di revisione (ad esempio,, la tua variabile dipendente sarebbe “exam performance”, misurata da 0-100 marchi, e la tua variabile indipendente sarebbe” revision time”, misurata in ore). In alternativa, è possibile utilizzare la regressione lineare per capire se il consumo di sigarette può essere previsto in base alla durata del fumo (cioè, la variabile dipendente sarebbe “consumo di sigarette”, misurata in termini di numero di sigarette consumate quotidianamente, e la variabile indipendente sarebbe “durata del fumo”, misurata in giorni). Se si dispone di due o più variabili indipendenti, piuttosto che una sola, è necessario utilizzare la regressione multipla., In alternativa, se si desidera solo stabilire se esiste una relazione lineare, è possibile utilizzare la correlazione di Pearson.
Nota: la variabile dipendente viene anche indicata come variabile di risultato, target o criterio, mentre la variabile indipendente viene anche indicata come variabile predittiva, esplicativa o regressore. In definitiva, qualunque sia il termine che usi, è meglio essere coerenti. Ci riferiremo a questi come variabili dipendenti e indipendenti in questa guida.,
In questa guida, vi mostriamo come effettuare regressione lineare utilizzando Stata, così come interpretare e riferire i risultati di questo test. Tuttavia, prima di presentarti questa procedura, devi capire le diverse ipotesi che i tuoi dati devono soddisfare affinché la regressione lineare ti dia un risultato valido. Discutiamo queste ipotesi dopo.
Stata
Ipotesi
Ci sono sette “ipotesi” che sono alla base della regressione lineare. Se una di queste sette ipotesi non viene soddisfatta, non è possibile analizzare i dati utilizzando linear perché non si otterrà un risultato valido., Poiché le ipotesi # 1 e #2 si riferiscono alla scelta delle variabili, non possono essere testate per l’utilizzo di Stata. Tuttavia, dovresti decidere se il tuo studio soddisfa queste ipotesi prima di andare avanti.
- Ipotesi #1: la variabile dipendente deve essere misurata a livello continuo., Esempi di tali variabili continue includono altezza (misurata in piedi e pollici), la temperatura (misurata in oC), retribuzione (misurato in dollari USA), revisione di tempo (misurato in ore), intelligenza (misurata con punteggio QI), il tempo di reazione (misurato in millisecondi), test di performance (misura da 0 a 100), vendita (misurata in numero di transazioni al mese), e così via. Se non sei sicuro che la tua variabile dipendente sia continua (cioè misurata a livello di intervallo o rapporto), consulta la nostra guida ai tipi di variabili.,
- Ipotesi # 2: la variabile indipendente deve essere misurata a livello continuo o categoriale. Tuttavia, se si dispone di una variabile indipendente categoriale, è più comune utilizzare un t-test indipendente (per 2 gruppi) o ANOVA a senso unico (per 3 gruppi o più). In caso di dubbi, esempi di variabili categoriali includono sesso (ad esempio, 2 gruppi: maschio e femmina), etnia (ad esempio, 3 gruppi: caucasico, afroamericano e ispanico), livello di attività fisica (ad esempio, 4 gruppi: sedentario, basso, moderato e alto) e professione (ad esempio,, 5 gruppi: chirurgo, medico, infermiere, dentista, terapeuta). In questa guida, ti mostriamo la procedura di regressione lineare e l’output di Stata quando entrambe le variabili dipendenti e indipendenti sono state misurate su un livello continuo.
Fortunatamente, puoi controllare le ipotesi #3, #4, #5, #6 e # 7 usando Stata. Quando si passa alle ipotesi #3, #4, #5, #6 e # 7, suggeriamo di testarli in questo ordine perché rappresenta un ordine in cui, se una violazione dell’ipotesi non è correggibile, non sarà più possibile utilizzare la regressione lineare., In effetti, non sorprenderti se i tuoi dati falliscono una o più di queste ipotesi poiché questo è abbastanza tipico quando si lavora con dati del mondo reale piuttosto che esempi di libri di testo, che spesso mostrano solo come eseguire la regressione lineare quando tutto va bene. Tuttavia, non preoccuparti perché anche quando i tuoi dati falliscono determinate ipotesi, c’è spesso una soluzione per superare questo (ad esempio, trasformando i tuoi dati o utilizzando invece un altro test statistico)., Basta ricordare che se non si verifica che i dati soddisfino queste ipotesi o si verifichino in modo errato, i risultati ottenuti durante l’esecuzione della regressione lineare potrebbero non essere validi.
- Ipotesi #3: deve esserci una relazione lineare tra le variabili dipendenti e indipendenti. Mentre ci sono un certo numero di modi per verificare se esiste una relazione lineare tra le tue due variabili, ti suggeriamo di creare un grafico a dispersione usando Stata, dove puoi tracciare la variabile dipendente contro la tua variabile indipendente., È quindi possibile ispezionare visivamente il grafico a dispersione per verificare la linearità. Il tuo scatterplot potrebbe essere simile a uno dei seguenti:
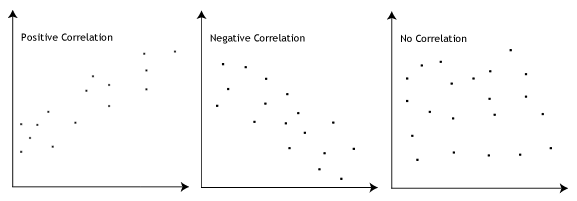
Se la relazione visualizzata nel tuo scatterplot non è lineare, dovrai eseguire un’analisi di regressione non lineare o “trasformare” i tuoi dati, cosa che puoi fare usando Stata.
- Ipotesi #4: non dovrebbero esserci valori anomali significativi. I valori anomali sono semplicemente singoli punti dati all’interno dei dati che non seguono il solito schema (ad esempio,, in uno studio di 100 punteggi IQ degli studenti, dove il punteggio medio era 108 con solo una piccola variazione tra gli studenti, uno studente aveva un punteggio di 156, che è molto insolito, e può anche metterla nel top 1% dei punteggi IQ a livello globale). I seguenti scatterplot evidenziare l’impatto potenziale dei valori anomali:
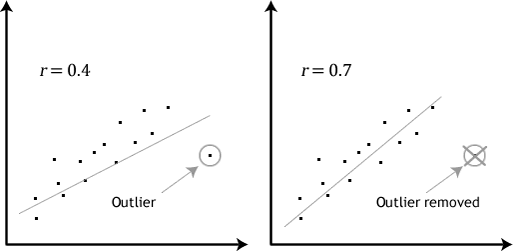
Il problema con outlier è che essi possono avere un effetto negativo sull’equazione di regressione che viene utilizzato per stimare il valore della variabile dipendente, basato su una variabile indipendente., Ciò cambierà l’output prodotto da Stata e ridurrà l’accuratezza predittiva dei risultati. Fortunatamente, è possibile utilizzare Stata per eseguire la diagnostica casewise per aiutare a rilevare possibili valori anomali.
- Ipotesi # 5: Dovresti avere l’indipendenza delle osservazioni, che puoi facilmente controllare usando la statistica Durbin-Watson, che è un semplice test da eseguire usando Stata.
- Ipotesi #6: i tuoi dati devono mostrare homoscedasticity, che è dove le varianze lungo la linea di best fit rimangono simili mentre ti muovi lungo la linea., I due scatterplot seguenti forniscono semplici esempi di dati che soddisfano questa ipotesi e uno che fallisce l’ipotesi:
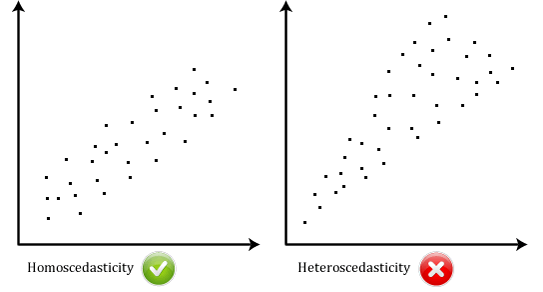
Quando analizzi i tuoi dati, sarai fortunato se il tuo scatterplot assomiglia a uno dei due sopra. Mentre questi aiutano a illustrare le differenze nei dati che soddisfano o violano l’ipotesi di omoscedasticità, i dati del mondo reale sono spesso molto più disordinati., È possibile verificare se i dati hanno mostrato omoscedasticità tracciando i residui standardizzati di regressione rispetto al valore predetto standardizzato di regressione.
- Ipotesi # 7: Infine, è necessario verificare che i residui (errori) della linea di regressione siano distribuiti approssimativamente normalmente. Due metodi comuni per verificare questa ipotesi includono l’utilizzo di un istogramma (con una curva normale sovrapposta) o di un grafico P-P normale.
In pratica, controllando le ipotesi #3, #4, #5, #6 e #7 probabilmente occuperà la maggior parte del tuo tempo quando esegui la regressione lineare., Tuttavia, non è un compito difficile, e Stata fornisce tutti gli strumenti necessari per farlo.
Nella sezione, Procedura, illustriamo la procedura Stata richiesta per eseguire la regressione lineare supponendo che non siano state violate ipotesi. In primo luogo, abbiamo esposto l’esempio che usiamo per spiegare la procedura di regressione lineare in Stata.
Stata
Esempio
Gli studi dimostrano che l’esercizio fisico può aiutare a prevenire le malattie cardiache. Entro limiti ragionevoli, più ti alleni, meno rischi di soffrire di malattie cardiache., Un modo in cui l’esercizio riduce il rischio di soffrire di malattie cardiache è riducendo un grasso nel sangue, chiamato colesterolo. Più ti alleni, più bassa è la concentrazione di colesterolo. Inoltre, è stato recentemente dimostrato che la quantità di tempo trascorso a guardare la TV – un indicatore di uno stile di vita sedentario – potrebbe essere un buon predittore di malattie cardiache (cioè, più TV si guarda, maggiore è il rischio di malattie cardiache).,
Pertanto, un ricercatore ha deciso di determinare se la concentrazione di colesterolo fosse correlata al tempo trascorso a guardare la TV in uomini altrimenti sani da 45 a 65 anni (una categoria di persone a rischio). Ad esempio, mentre le persone trascorrevano più tempo a guardare la TV, aumentava anche la loro concentrazione di colesterolo (una relazione positiva); o accadeva il contrario? Il ricercatore voleva anche conoscere la proporzione di concentrazione di colesterolo che il tempo trascorso a guardare la TV potrebbe spiegare, oltre ad essere in grado di prevedere la concentrazione di colesterolo., Il ricercatore potrebbe quindi determinare se, ad esempio, le persone che trascorrevano otto ore a guardare la TV al giorno avessero livelli pericolosamente alti di concentrazione di colesterolo rispetto alle persone che guardavano solo due ore di TV.
Per effettuare l’analisi, il ricercatore ha reclutato 100 partecipanti maschi sani di età compresa tra 45 e 65 anni. La quantità di tempo trascorso a guardare la TV (cioè la variabile indipendente, time_tv) e la concentrazione di colesterolo (cioè la variabile dipendente, colesterolo) sono state registrate per tutti i partecipanti 100., Espresso in termini variabili, il ricercatore voleva regredire il colesterolo su time_tv.
Nota: L’esempio e i dati utilizzati per questa guida sono fittizi. Li abbiamo appena creati ai fini di questa guida.
Stata
Imposta in Stata
Nota: non importa se si crea prima la variabile dipendente o indipendente.
Dopo aver creato queste due variabili – time_tv e colesterolo – abbiamo inserito i punteggi per ciascuna nelle due colonne del foglio di calcolo Data Editor (Edit) (cioè, il tempo , in ore, che i partecipanti hanno guardato la TV nella colonna di sinistra (cioè, time_tv, la variabile indipendente), di partecipanti e la concentrazione di colesterolo nel mmol/L nella colonna di destra (cioè, il colesterolo, la variabile dipendente), come mostrato di seguito:
Pubblicato con il permesso scritto da StataCorp LP.,
Stata
Procedura di test in Stata
In questa sezione, ti mostriamo come analizzare i tuoi dati usando la regressione lineare in Stata quando le sei ipotesi nella sezione precedente, Supposizioni, non sono state violate. È possibile eseguire la regressione lineare utilizzando il codice o l’interfaccia utente grafica (GUI) di Stata. Dopo aver effettuato la tua analisi, ti mostriamo come interpretare i tuoi risultati. Innanzitutto, scegliere se si desidera utilizzare il codice o l’interfaccia utente grafica (GUI) di Stata.,
Codice
Il codice per effettuare la regressione lineare sui dati assume la forma:
regredire DependentVariable IndependentVariable
Questo codice è inserito nel box qui sotto:
Pubblicato con il permesso scritto da StataCorp LP.,
Utilizza il nostro esempio in cui la variabile dipendente è il colesterolo e la variabile indipendente è time_tv, il codice sarà:
regredire colesterolo time_tv
Nota 1: È necessario essere precisi quando si immette il codice casella. Il codice è “case sensitive”. Ad esempio, se hai inserito “Colesterolo” dove la “C” è maiuscola piuttosto che minuscola (cioè, una piccola “c”), che dovrebbe essere, si otterrà un messaggio di errore come il seguente:
Nota 2: Se si sta ancora ricevendo il messaggio di errore nella Nota 2: sopra, vale la pena di controllare il nome che avete dato il vostro due variabili in un Editor di Dati quando si imposta il tuo file (cioè, vedere l’Editor di Dati a schermo sopra)., Nella casella sul lato destro della schermata dell’Editor dei dati, è il modo in cui hai scritto le tue variabili nella sezione
, non la sezione
che devi inserire nel codice (vedi sotto per la nostra variabile dipendente). Questo può sembrare ovvio, ma è un errore che a volte viene fatto, con conseguente errore nella Nota 2 sopra.
Quindi, inserire il codice, regredire colesterolo time_tv, e premere il tasto “Return/Enter” sulla tastiera.,
Pubblicato con il permesso scritto di StataCorp LP.
Puoi vedere l’output di Stata che verrà prodotto qui.,
Interfaccia Utente Grafica (GUI)
I tre passaggi necessari per effettuare la regressione lineare in Stata 12 e 13 sono riportati di seguito:
- fare Clic su Statistiche > modelli Lineari e le relative > regressione Lineare nel menu principale, come mostrato di seguito:
Pubblicato con il permesso scritto da StataCorp LP.,
Ti verrà presentata la finestra di dialogo Regress – Linear regression:
Pubblicata con il permesso scritto di StataCorp LP.
- Selezionare colesterolo all’interno della variabile dipendente: casella a discesa, e time_tv all’interno delle variabili indipendenti: casella a discesa. Si finirà con la seguente schermata:
Pubblicato con il permesso scritto di StataCorp LP.,
-
Fare clic sul pulsante
. Questo genererà l’output.
Stata
Output dell’analisi di regressione lineare in Stata
Se i tuoi dati passavano all’ipotesi #3 (cioè, c’era una relazione lineare tra le tue due variabili), #4 (cioè, non c’erano valori anomali significativi), ipotesi #5 (cioè, avevi indipendenza delle osservazioni), ipotesi #6 (cioè, i tuoi dati mostravano omoscedasticità) cioè,, i residui (errori) erano approssimativamente distribuiti normalmente), che abbiamo spiegato in precedenza nella sezione Assunzioni, sarà sufficiente interpretare il seguente output di regressione lineare in Stata:
Pubblicato con il permesso scritto di StataCorp LP.,
L’output consiste di quattro importanti informazioni: (a) il valore R2 (riga”R-squared”) rappresenta la proporzione di varianza nella variabile dipendente che può essere spiegata dalla nostra variabile indipendente (tecnicamente è la proporzione di variazione rappresentata dal modello di regressione al di sopra e al di là del modello medio). Tuttavia, R2 si basa sul campione ed è una stima positivamente parziale della proporzione della varianza della variabile dipendente rappresentata dal modello di regressione (cioè, è troppo grande); (b) un adeguato valore di R2 (Adj R-squared” riga), che corregge la polarizzazione positiva per fornire un valore che potrebbe essere previsto nella popolazione; (c) il valore di F, i gradi di libertà (“F( 1, 98)”) e la significatività statistica del modello di regressione (“Prob > F in corrispondenza della riga”); e (d) i coefficienti per il costante e variabile indipendente (“Coef.”colonna), che è l’informazione necessaria per prevedere la variabile dipendente, colesterolo, utilizzando la variabile indipendente, time_tv.
In questo esempio, R2 = 0.151. Rettificato R2 = 0,143 (a 3 d.p.,), il che significa che la variabile indipendente, time_tv, spiega il 14,3% della variabilità della variabile dipendente, il colesterolo, nella popolazione. R2 rettificato è anche una stima della dimensione dell’effetto, che a 0,143 (14,3%), è indicativa di una dimensione media dell’effetto, secondo la classificazione di Cohen (1988). Tuttavia, normalmente è R2 non il R2 rettificato che viene riportato nei risultati. In questo esempio, il modello di regressione è statisticamente significativo, F (1, 98) = 17.47, p = .0001., Ciò indica che, nel complesso, il modello applicato può prevedere in modo statisticamente significativo la variabile dipendente, il colesterolo.
Nota: Presentiamo l’output dell’analisi di regressione lineare sopra. Tuttavia, poiché dovresti aver testato i tuoi dati per le ipotesi che abbiamo spiegato in precedenza nella sezione Assunzioni, dovrai anche interpretare l’output di Stata prodotto quando hai testato queste ipotesi. Questo include: (a) i grafici a dispersione che hai usato per verificare se c’era una relazione lineare tra le tue due variabili (cioè,, Assunzione #3); (b) casewise diagnostica per verificare che non ci sono state significative outlier (cioè, l’Assunzione, #4); (c) l’uscita dal Durbin-Watson statistica per verificare l’indipendenza delle osservazioni (cioè, l’Assunzione, #5); (d) una dispersione di regressione standardizzati residui contro la regressione standardizzati valore stimato per determinare se i dati hanno mostrato homoscedasticity (cioè, l’Assunzione, #6); e un istogramma (con sovrapposta curva normale) e Normale P-P Plot per verificare se i residui (errori) sono stati circa distribuiti normalmente (cioè, l’Assunzione, #7)., Inoltre, ricorda che se i tuoi dati falliscono una di queste ipotesi, l’output che ottieni dalla procedura di regressione lineare (cioè l’output di cui discutiamo sopra) non sarà più rilevante e potresti dover eseguire un test statistico diverso per analizzare i tuoi dati.,
Stata
creazione di output dell’analisi di regressione lineare
Quando si segnala l’uscita del vostro regressione lineare, è una buona pratica includere: (a) un’introduzione all’analisi effettuata; (b) informazioni circa il vostro campione, comprese eventuali valori mancanti; (c) l’osservato F-valore, i gradi di libertà e il livello di significatività (cioè, il p-value); (d) la percentuale di variabilità della variabile dipendente spiegata dalla variabile indipendente (cioè, il vostro Adjusted R2 ); e (e) l’equazione di regressione per il tuo modello., Sulla base dei risultati di cui sopra, potremmo riportare i risultati di questo studio come segue:
- Generale
Una regressione lineare ha stabilito che il tempo giornaliero trascorso a guardare la TV potrebbe prevedere in modo statisticamente significativo la concentrazione di colesterolo, F(1, 98) = 17.47, p = .0001 e il tempo trascorso a guardare la TV hanno rappresentato il 14,3% della variabilità spiegata nella concentrazione di colesterolo. L’equazione di regressione era: concentrazione di colesterolo prevista = -2.135 + 0.044 x (tempo trascorso a guardare la TV).,
Oltre a riportare i risultati come sopra, è possibile utilizzare un diagramma per presentare visivamente i risultati. Ad esempio, è possibile farlo utilizzando uno scatterplot con intervalli di sicurezza e previsione (anche se non è molto comune aggiungere l’ultimo). Questo può rendere più facile per gli altri a capire i risultati. Inoltre, è possibile utilizzare l’equazione di regressione lineare per fare previsioni sul valore della variabile dipendente in base a diversi valori della variabile indipendente., Mentre Stata non produce questi valori come parte della procedura di regressione lineare di cui sopra, c’è una procedura in Stata che è possibile utilizzare per farlo.