|
|
Variancia intézkedések milyen messze egy adatokra terjed ki. A nulla variancia azt jelzi, hogy az összes adatérték azonos. Minden nem nulla eltérés pozitív.
|
egy kis szórás azt jelzi, hogy az adatpontok általában nagyon közel állnak az átlaghoz és egymáshoz., A nagy variancia azt jelzi, hogy az adatpontok nagyon elterjedtek az átlagtól, egymástól. A variancia az egyes pontoktól az átlagig terjedő négyzetek átlaga.
Az egyetlen különbség a távolságok négyzete.
folyamat: (1) Keresse meg a készlet átlagát (átlagát). (2) vonja le az egyes adatértékeket az átlagból, hogy megtalálja a távolságot az átlagtól. (3) tér minden távolság. (4) Adja hozzá a távolságok összes négyzetét., (4) Oszd meg az adatok darabszámával (a népesség varianciájára).
a variancia egyik problémája az, hogy nem rendelkezik ugyanolyan mértékegységgel, mint az eredeti adatok. Például a lábakban mért hosszúságot tartalmazó eredeti adatok négyzetlábban mért varianciával rendelkeznek.,
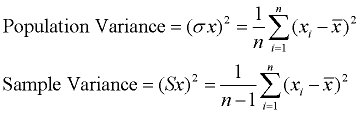 |
 |
|
![]()
|
|
szórás azt mutatja, hogy mennyi variáció (diszperziós, elterjedt, scatter) a gonosz létezik., Ez egy “tipikus” eltérést jelent az átlagtól. Ez a variabilitás népszerű mértéke, mivel visszatér az adatkészlet eredeti mértékegységeihez.
|
az alacsony szórás azt jelzi, hogy az adatpontok általában nagyon közel állnak az átlaghoz. A magas szórás azt jelzi, hogy az adatpontok nagy értéktartományban vannak elosztva.
a szórás úgy tekinthető ,mint egy “standard” módja annak, hogy tudjuk, mi a normális (tipikus), mi a nagyon nagy, és mi nagyon kicsi az adatkészletben.,
a szórás a variabilitás népszerű mértéke, mivel visszatér az adatkészlet eredeti mértékegységeihez. Például a lábakban mért hosszúságot tartalmazó eredeti adatok standard eltérést mutatnak a lábakban is.,
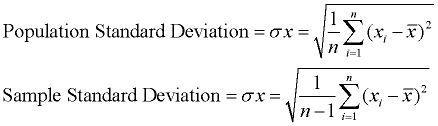 |
 |
|
a szórás egyszerűen a szórás négyzetgyöke. Ez a leírás a lakosság szórásának kiszámítására szolgál. Ha Minta szórásra van szükség, oszd meg n-1-vel n helyett., Mivel a szórás a variancia négyzetgyöke, először ki kell számítanunk a varianciát. |
|
|
1. Keresse meg az átlagot.
|
|
|
2. Minden adatértékből kivonjuk az átlagot, és négyzetbe állítjuk ezeket a különbségeket (a négyzetes különbségek).
|
|
|
3. Keresse meg a négyzetes különbségek átlagát (adja hozzá őket, majd ossza meg az adatértékek számával). Ez lesz a variancia.,
|
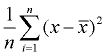 variancia |
|
4. Vegyük a négyzetgyökét. Ez lesz a lakosság szórása. Kerekítse a választ a probléma irányai szerint.
|
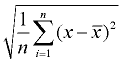 szórás |
![]()
![]() normál görbe
normál görbe
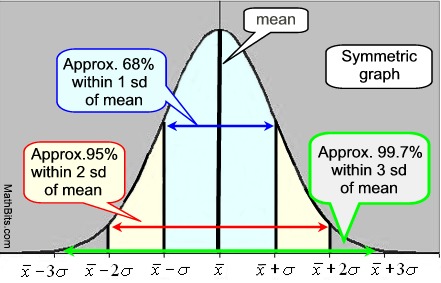
a normál görbe szimmetrikus, harang alakú görbe., A gráf középpontja az átlag, a gráf magasságát és szélességét pedig a szórás határozza meg. Ha a szórás kicsi,a görbe magas és keskeny lesz. Ha a szórás nagy, a görbe rövid és széles lesz. Az átlag és a medián értéke egy normál görbében azonos.
|
normál görbe empirikus szabály: * az adatok 68% – a az átlag egy szórásán belül található., * az adatok 95% – a az átlag két szórásán belül van. * az adatok 99,7% – a az átlag három szórásán belül van. IQR normál görbe esetén 1,34896 x szórás. |
 |
![]()
