Support Vector Machine vagy SVM az egyik legnépszerűbb felügyelt tanulási algoritmusok, amelyeket a besorolás, valamint a regressziós problémák. Elsősorban azonban a gépi tanulás osztályozási problémáira használják.
az SVM algoritmus célja a legjobb vonal-vagy döntési határ létrehozása, amely az n-dimenziós teret osztályokba különítheti el, hogy az új adatpontot a megfelelő kategóriába tudjuk helyezni a jövőben., Ezt a legjobb döntési határt hiperplánnak nevezik.
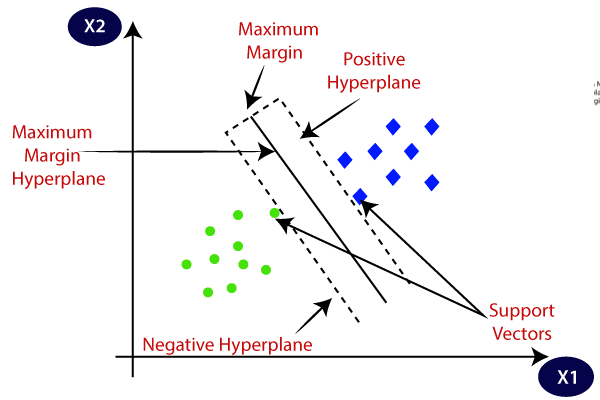
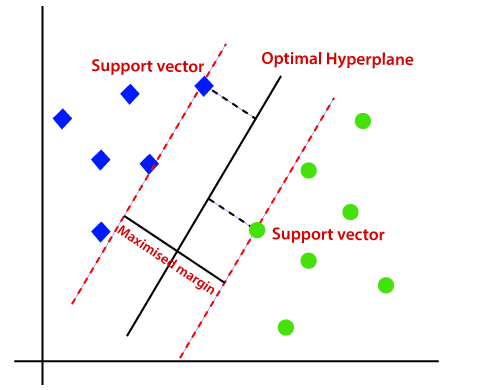
az SVM kiválasztja azokat a szélsőséges pontokat / vektorokat, amelyek segítenek a hiperplán létrehozásában. Ezeket a szélsőséges eseteket támogató vektoroknak nevezik, ezért az algoritmust támogató Vektor gépnek nevezik. Tekintsük az alábbi diagramot, amelyben két különböző kategória van osztályozva döntési határral vagy hiperplánnal:
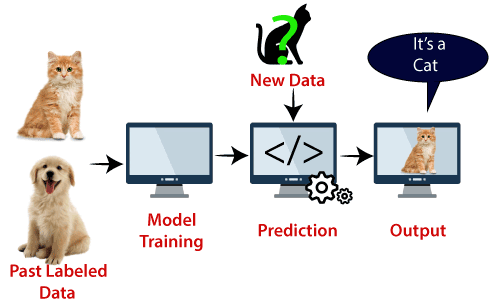
példa: SVM megérthető azzal a példával, amelyet a KNN osztályozóban használtunk., Tegyük fel, hogy egy furcsa macskát látunk, amely a kutyák néhány jellemzőjével is rendelkezik, tehát ha olyan modellt akarunk, amely pontosan meg tudja határozni, hogy macska vagy kutya, akkor egy ilyen modellt az SVM algoritmus segítségével lehet létrehozni. Mi lesz az első vonat a modell sok kép a macskák és kutyák, hogy meg tudja tanulni a különböző funkciók a macskák és kutyák, majd teszteljük ezt a furcsa lény. Tehát, mivel a támogató vektor döntési határt hoz létre e két adat (macska és kutya) között, és szélsőséges eseteket választ (támogató Vektorok), látni fogja a macska és a kutya szélsőséges esetét., A támogató Vektorok alapján macskaként osztályozza. Vegye figyelembe az alábbi ábrát:
SVM algoritmus használható arcfelismeréshez, képosztályozáshoz, szöveg kategorizáláshoz stb.
típusú SVM
SVM lehet két típusa van:
- lineáris SVM: lineáris SVM használják lineárisan elválasztható adatok, ami azt jelenti,ha egy adathalmaz lehet besorolni két osztályba segítségével egy egyenes vonal, akkor az ilyen adatokat nevezzük lineárisan elválasztható adatok, és osztályozó nevezzük lineáris SVM osztályozó.,
- nemlineáris SVM: a nemlineáris SVM-et nem lineárisan elválasztott adatokra használják, ami azt jelenti, hogy ha egy adatkészletet nem lehet egyenes vonal használatával osztályozni, akkor az ilyen adatokat nem lineáris adatoknak nevezzük, és az alkalmazott osztályozót nemlineáris SVM osztályozónak nevezzük.
Hyperplane és Support Vektorok az SVM algoritmusban:
Hyperplane: több sor / döntési határ lehet az osztályok elkülönítésére n-dimenziós térben, de meg kell találnunk a legjobb döntési határt, amely segít az adatpontok osztályozásában. Ez a legjobb határ az SVM hyperplane néven ismert.,
a hyperplane méretei az adatkészletben található funkcióktól függenek, ami azt jelenti, hogy ha 2 funkció van (a képen látható módon), akkor a hyperplane egyenes vonal lesz. Ha pedig 3 funkció van, akkor a hyperplane egy 2 dimenziós sík lesz.
mindig létrehozunk egy hiperlapot, amelynek maximális margója van, ami az adatpontok közötti maximális távolságot jelenti.
Support Vektorok:
a hiperplánhoz legközelebb eső és a hiperplán helyzetét befolyásoló adatpontokat vagy vektorokat támogató vektornak nevezzük., Mivel ezek a vektorok támogatják a hyperplane-t, ezért támogató vektornak nevezik.
hogyan működik az SVM?
lineáris SVM:
az SVM algoritmus működése egy példa segítségével érthető meg. Tegyük fel, hogy van egy adatkészletünk, amelynek két címkéje van (zöld és kék), az adatkészletnek pedig két x1 és x2 funkciója van. Olyan osztályozót akarunk, amely a koordináták párját(x1, x2) zöld vagy kék színnel osztályozhatja. Tekintsük az alábbi képet:
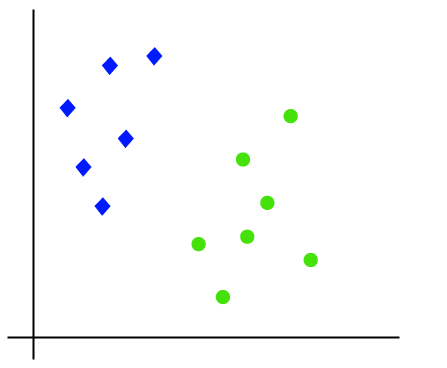
Tehát mivel 2-d hely, így csak egy egyenes vonal használatával könnyen elválaszthatjuk ezt a két osztályt., De lehet több sor, amely elválaszthatja ezeket az osztályokat. Tekintsük az alábbi képet:
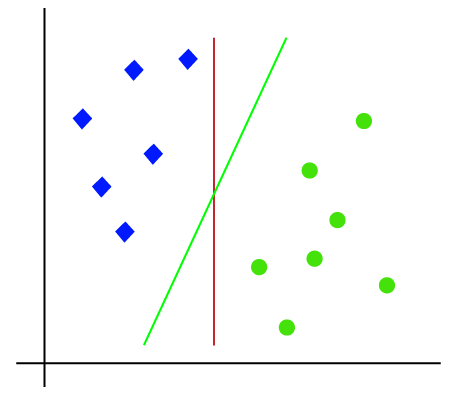
ezért az SVM algoritmus segít megtalálni a legjobb vonal-vagy döntési határt; ezt a legjobb határt vagy régiót hiperplánnak nevezik. Az SVM algoritmus mindkét osztályból megtalálja a vonalak legközelebbi pontját. Ezeket a pontokat támogató vektoroknak nevezik. A vektorok és a hiperplán közötti távolságot margónak nevezzük. Az SVM célja, hogy maximalizálja ezt a margót. A maximális margóval rendelkező hiperplánt az optimális hiperplánnak nevezik.,
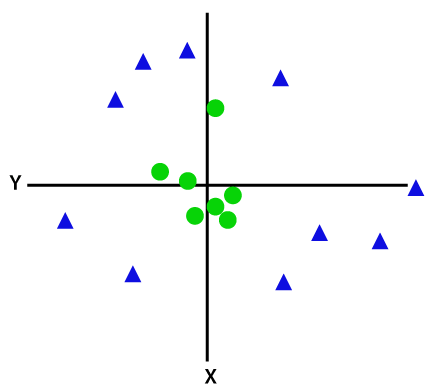
nemlineáris SVM:
Ha az adatok lineárisan vannak elrendezve, akkor egyenes vonal segítségével elválaszthatjuk, de nem lineáris adatok esetén nem tudunk egyetlen egyenes vonalat rajzolni. Tekintsük az alábbi képet:
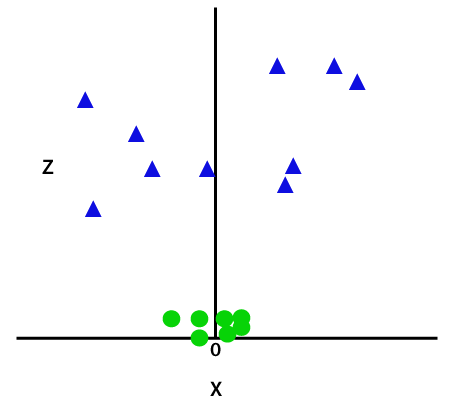
tehát ezeknek Az adatpontoknak a szétválasztásához még egy dimenziót kell hozzáadnunk. A lineáris adatoknál két X és y dimenziót használtunk, így a nemlineáris adatoknál egy harmadik z dimenziót adunk hozzá., A következő módon számítható ki:
z=x2 +y2
a harmadik dimenzió hozzáadásával a mintaterület a kép alatt lesz:
tehát most az SVM az adatkészleteket osztályokra osztja a következő módon. Tekintsük az alábbi képet:
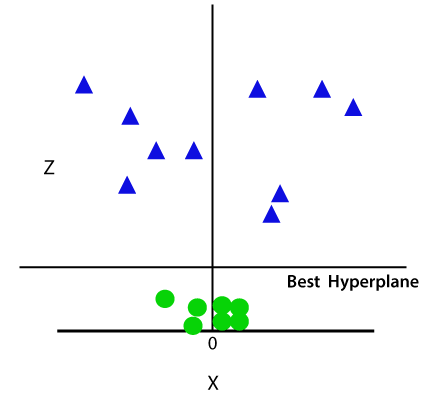
mivel 3-d térben vagyunk, ezért úgy néz ki, mint egy sík, amely párhuzamos az x tengelygel. Ha 2D térben konvertáljuk z=1-rel, akkor a következő lesz:
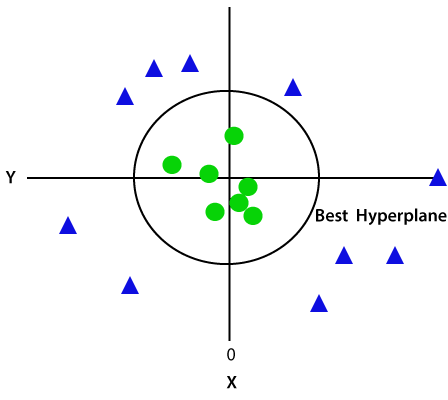
ezért nem lineáris adatok esetén az 1 sugár kerületét kapjuk.,
python Support Vector Machine megvalósítása
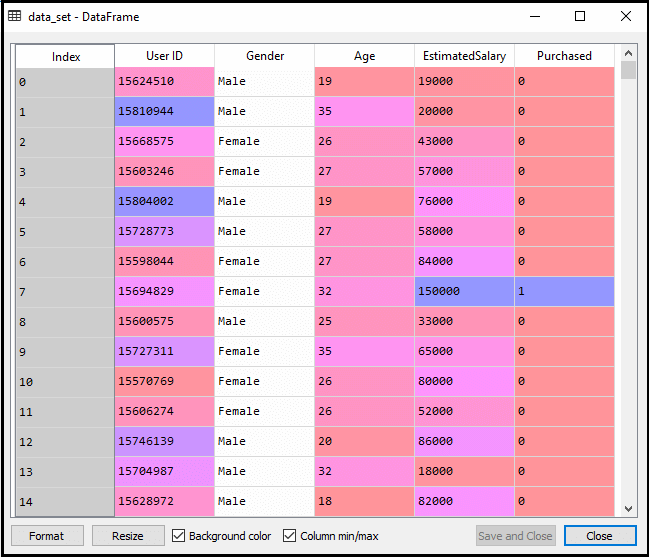
most implementáljuk az SVM algoritmust a Python használatával. Itt ugyanazt az adatkészletet fogjuk használni user_data, amit a logisztikus regresszióban és KNN osztályozásban használtunk.
- adatfeldolgozási lépés
az adatfeldolgozás előtti lépésig a kód ugyanaz marad. Az alábbiakban található a kód:
a fenti kód végrehajtása után előre feldolgozzuk az adatokat., A kód az adatkészletet a következőképpen adja meg:
a tesztkészlet méretezett kimenete a következő lesz:
az SVM osztályozó felszerelése a képzési készlethez:
most a képzési készlet az SVM osztályozóhoz lesz felszerelve. Az SVM osztályozó létrehozásához importáljuk az SVC osztályt a Sklearn-ból.svm könyvtár. Az alábbiakban található a kód:
a fenti kódban kernel=’lineáris’ – t használtunk, mivel itt SVM-et hozunk létre lineárisan elválasztható adatokhoz. A nemlineáris adatok esetében azonban megváltoztathatjuk., Ezután illesztettük az osztályozót a képzési adatkészlethez (x_train, y_train)
kimenet:
a modell teljesítménye megváltoztatható a C(Regularizációs tényező), a gamma és a kernel értékének megváltoztatásával.
- a tesztkészlet eredményének előrejelzése:
most megjósoljuk a tesztkészlet kimenetét. Ehhez létrehozunk egy új vektort y_pred. Az alábbiakban a kód:
miután megkaptuk az y_pred vektort, összehasonlíthatjuk az y_pred és y_test eredményét, hogy ellenőrizzük a tényleges érték és az előre jelzett érték közötti különbséget.,
kimenet: az alábbiakban a tesztkészlet előrejelzésének kimenete található:

- a zavartmátrix létrehozása:
most látni fogjuk az SVM osztályozó teljesítményét, hogy hány helytelen előrejelzés van a logisztikai regressziós osztályozóhoz képest. A zavart mátrix létrehozásához importálnunk kell a sklearn könyvtár confusion_matrix funkcióját. A funkció importálása után egy új cm változó használatával hívjuk meg. A függvény két paramétert vesz fel, elsősorban y_true( a tényleges értékek) és y_pred (az osztályozó által megcélzott értékvisszatérítés)., Az alábbiakban látható a kód:
kimenet:
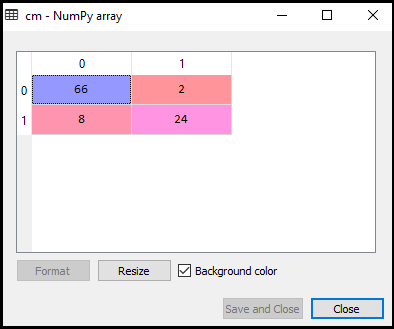
amint az a fenti kimeneti képen látható, 66+24= 90 helyes előrejelzés és 8+2= 10 helyes előrejelzés található. Ezért azt mondhatjuk, hogy SVM modellünk javult a logisztikai regressziós modellhez képest.,
- Megjelenítésére, a képzés meghatározott eredmény:
Most képzeld el a képzési meghatározott eredmény, az alábbiakban a kód hozzá:
Teljesítmény:
a végrehajtó a fenti kódot, mi lesz a kimenet, mint:
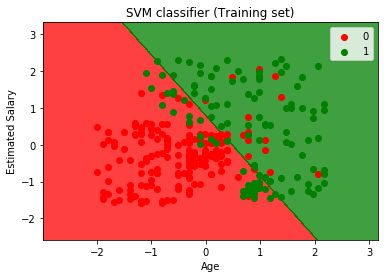
Mint láthatjuk, a fenti kimenet megjelenő hasonló a Logisztikai regressziós kimenet. A kimenetben az egyenes vonalat hipertervként kaptuk, mert lineáris kernelt használtunk az osztályozóban. A fentiekben azt is megvitattuk, hogy a 2D tér esetében az SVM hyperplane egyenes vonal.,
- a tesztkészlet eredményének megjelenítése:
kimenet:
a fenti kód végrehajtásával a kimenetet kapjuk:
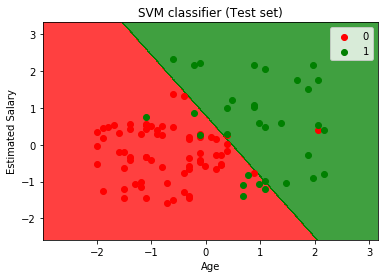
amint a fenti kimeneti képen látható, az SVM osztályozó két régióra osztotta a felhasználókat (vásárolt vagy nem vásárolt). Azok a felhasználók, akik megvásárolták a SUV-t, a piros scatter pontokkal rendelkező piros régióban vannak. Azok a felhasználók, akik nem vásárolták meg a SUV-t, a zöld régióban vannak, zöld szórási pontokkal. A hyperplane a két osztályt vásárolt és nem vásárolt változókra osztotta.