Bevezetés
lineáris regresszió, más néven egyszerű lineáris regresszió vagy bivariate lineáris regresszió, akkor használjuk, ha azt akarjuk, hogy megjósolni az érték egy függő változó értékén alapuló független változó. Például lineáris regresszió segítségével megértheti, hogy a vizsga teljesítménye a felülvizsgálati idő alapján megjósolható-e (azaz,, a függő változó lenne “vizsga teljesítmény”, mért 0-100 jelek, a független változó lenne” felülvizsgálati idő”, mért óra). Felváltva, akkor használja a lineáris regresszió, hogy megértsük, hogy a cigaretta fogyasztás előre jelezhető alapján a dohányzás időtartama (azaz a függő változó a “cigaretta-fogyasztás” mért számát tekintve cigarettát fogyasztott napi, illetve a független változó lenne “a dohányzás időtartama” mért nap). Ha két vagy több Független változója van, nem csak egy, akkor több regressziót kell használnia., Alternatív megoldásként, ha csak azt szeretné megállapítani, hogy létezik-e lineáris kapcsolat, használhatja Pearson korrelációját.
Megjegyzés: A függő változót eredmény, cél vagy kritérium változónak is nevezik, míg a független változót prediktornak, magyarázó vagy regresszor változónak is nevezik. Végül, bármelyik kifejezést használja, a legjobb, ha következetes. Ezeket az útmutatóban függő és független változóknak fogjuk tekinteni.,
ebben az útmutatóban megmutatjuk, hogyan lehet lineáris regressziót végrehajtani Stata használatával, valamint értelmezni és jelenteni a teszt eredményeit. Mielőtt azonban bemutatnánk ezt az eljárást, meg kell értenie azokat a különböző feltételezéseket, amelyeknek az adatoknak meg kell felelniük ahhoz, hogy a lineáris regresszió érvényes eredményt adjon. Megvitatjuk ezeket a feltételezéseket.
Stata
feltételezések
hét” feltételezés ” létezik, amelyek alátámasztják a lineáris regressziót. Ha a hét feltételezés közül bármelyik nem teljesül, akkor nem elemezheti adatait linear segítségével, mert nem kap érvényes eredményt., Mivel az 1. és a 2. feltételezések a változók megválasztására vonatkoznak, nem tesztelhetők a Stata használatára. A továbblépés előtt azonban el kell döntenie, hogy tanulmánya megfelel-e ezeknek a feltételezéseknek.
- 1. feltételezés: a függő változót folyamatos szinten kell mérni., Példák az ilyen folytonos változók közé magasság (mért hüvelykben), hőmérséklet (mért oC), illetmény (mért usa dollár), a revízió idő (mért óra), az intelligencia (mérni, IQ), reakció idő (mért ezredmásodpercben), teszt teljesítmény (mért 0-tól 100-ig), értékesítés (mért a tranzakciók száma havonta), stb. Ha nem biztos benne ,hogy a függő változója folyamatos-e (azaz intervallum vagy Arány szintjén mérve), olvassa el a változó útmutató típusait.,
- 2. feltételezés: a független változót folyamatos vagy kategorikus szinten kell mérni. Ha azonban van egy kategorikus független változó, gyakoribb egy független t-teszt (2 csoport esetében) vagy egyirányú ANOVA (3 vagy több csoport esetében) használata. Abban az esetben, ha nem biztos benne, a kategorikus változók példái közé tartozik a nem (pl. 2 csoport: férfi és nő), az etnikai hovatartozás (pl. 3 csoport: kaukázusi, afroamerikai és spanyol), a fizikai aktivitás szintje (pl. 4 csoport: ülő, alacsony, mérsékelt és magas), valamint a szakma (pl.,, 5 csoport: sebész, orvos, nővér, fogorvos, terapeuta). Ebben az útmutatóban megmutatjuk a lineáris regressziós eljárást és a Stata kimenetet, amikor mind a függő, mind a független változókat folyamatos szinten mértük.
szerencsére ellenőrizheti a feltételezéseket #3, #4, #5, #6 és # 7 segítségével Stata. Amikor továbblépünk a feltételezésekre #3, #4, #5, #6 és #7, Azt javasoljuk, hogy teszteljék őket ebben a sorrendben, mert olyan sorrendet képvisel, ahol, ha a feltételezés megsértése nem javítható, akkor már nem lesz képes lineáris regressziót használni., Valójában, ne lepődj meg, ha az adatok nem egy vagy több ilyen feltételezések, mivel ez meglehetősen jellemző, ha dolgozik valós adatok helyett tankönyv példák, amelyek gyakran csak azt mutatják, hogyan kell elvégezni lineáris regresszió, ha minden jól megy. Ne aggódjon azonban, mert még akkor is, ha az adatok bizonyos feltételezéseket meghiúsulnak, gyakran van megoldás ennek leküzdésére (például az adatok átalakítására vagy egy másik statisztikai teszt használatára)., Ne feledje, hogy ha nem ellenőrzi, hogy az adatok megfelelnek-e ezeknek a feltételezéseknek, vagy helytelenül teszteli őket, előfordulhat, hogy a lineáris regresszió futtatásakor kapott eredmények nem érvényesek.
- 3. feltételezés: lineáris összefüggésre van szükség a függő és a független változók között. Bár számos módja van annak ellenőrzésére, hogy létezik-e lineáris kapcsolat a két változó között, javasoljuk egy scatterplot létrehozását Stata használatával, ahol a függő változót a független változóval ábrázolhatja., Ezután vizuálisan ellenőrizheti a szórólapot, hogy ellenőrizze a linearitást. A scatterplot úgy néz ki, mint az alábbi:
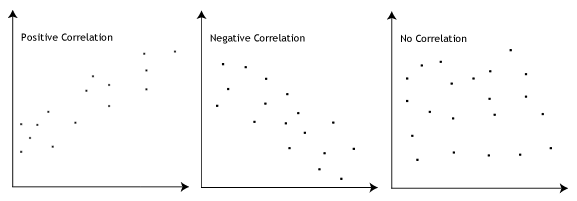
Ha a scatterplotban megjelenített kapcsolat nem lineáris, akkor nem lineáris regressziós elemzést kell futtatnia, vagy” átalakítania ” az adatait, amit a Stata használatával tehet meg.
- 4. feltételezés :nem lehet jelentős kiugró. A kiugró értékek egyszerűen egyetlen adatpont az Ön adatain belül, amelyek nem követik a szokásos mintát (pl.,, egy tanulmány 100 diák IQ pontszámok, ahol az átlagos pontszám volt 108 csak egy kis különbség a diákok között, egy diák volt a pontszám 156, ami nagyon szokatlan, és még fel neki a felső 1% IQ pontszámok világszerte). A következő szórólapok kiemelik a kiugrók lehetséges hatását:
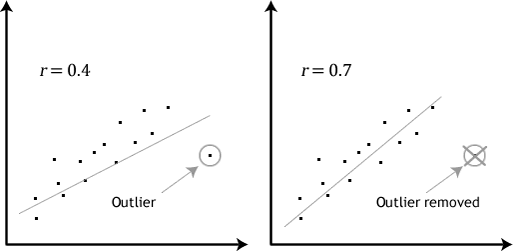
a kiugró értékek problémája az, hogy negatív hatással lehetnek a regressziós egyenletre, amelyet a függő változó értékének a független változó alapján történő előrejelzésére használnak., Ez megváltoztatja a stata által termelt kimenetet, és csökkenti az eredmények prediktív pontosságát. Szerencsére a Stata segítségével casewise diagnosztikát végezhet, hogy segítsen felismerni a lehetséges kiugrókat.
- 5. feltételezés: függetlennek kell lennie a megfigyelésektől, amelyeket könnyen ellenőrizhet a Durbin-Watson statisztika segítségével, amely egy egyszerű teszt a Stata használatával.
- 6. feltételezés: az adatoknak homoscedasticitást kell mutatniuk,ahol a legjobb illeszkedési vonal mentén lévő eltérések hasonlóak maradnak a vonal mentén., Az alábbi két scatterplot egyszerű példákat nyújt az adatokra, amelyek megfelelnek ennek a feltételezésnek, és amelyek elmulasztják a feltételezést:
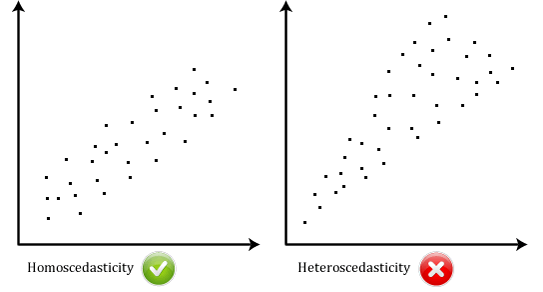
Ha saját adatait elemzi, akkor szerencsés lesz, ha a scatterplot a fenti kettő egyikére hasonlít. Míg ezek segítenek szemléltetni az adatok közötti különbségeket, amelyek megfelelnek vagy megsértik a homoscedasticitás feltételezését, a valós adatok gyakran sokkal rendetlenebbek., Ellenőrizheti, hogy az adatok homoscedasticity-t mutattak-e a regressziós szabványosított maradványok ábrázolásával a regressziós szabványosított előre jelzett értékhez képest.
- 7. feltételezés: végül ellenőriznie kell, hogy a regressziós vonal maradékai (hibák) általában eloszlanak-e. Ennek a feltételezésnek a ellenőrzésére két közös módszer magában foglalja a hisztogram (egymásra helyezett normál görbével) vagy a normál P-P telek használatát.
a gyakorlatban a feltételezések ellenőrzése#3, #4, #5, #6 a # 7 valószínűleg a legtöbb időt veszi igénybe lineáris regresszió végrehajtásakor., Ez azonban nem nehéz feladat, a Stata pedig minden szükséges eszközt biztosít ehhez.
a szakasz, eljárás, bemutatjuk a Stata eljárás végrehajtásához szükséges lineáris regresszió feltételezve, hogy nem feltételezések megsértették. Először bemutatjuk azt a példát, amelyet a lineáris regressziós eljárás magyarázatára használunk Stata-ban.
Stata
példa
tanulmányok azt mutatják, hogy a testmozgás segíthet megelőzni a szívbetegségeket. Ésszerű határokon belül, minél többet gyakorol, annál kisebb a kockázata annak, hogy szívbetegségben szenved., Az egyik módja annak, hogy a testmozgás csökkenti a szívbetegségben szenvedők kockázatát, a vér zsírjának csökkentése, az úgynevezett koleszterin. Minél többet gyakorol, annál alacsonyabb a koleszterin koncentrációja. Ezenkívül a közelmúltban kimutatták, hogy a tévénézés – az ülő életmód mutatója – a szívbetegség jó előrejelzője lehet (azaz minél több TV-t néz, annál nagyobb a szívbetegség kockázata).,
ezért egy kutató úgy döntött, hogy meghatározza, hogy a koleszterin koncentrációja összefügg-e az egyébként egészséges 45-65 éves férfiak TÉVÉNÉZÉSÉVEL töltött idővel (az emberek veszélyeztetett kategóriája). Például, mivel az emberek több időt töltöttek tévénézéssel, a koleszterin koncentrációja is nőtt (pozitív kapcsolat); vagy éppen ellenkezőleg történt? A kutató azt is meg akarta tudni, hogy a koleszterin-koncentráció aránya, amelyet a tévénézés során töltött idő magyarázhat, valamint képes megjósolni a koleszterin koncentrációját., A kutató ezután meghatározhatja, hogy például azok az emberek, akik napi nyolc órát töltöttek tévénézéssel, veszélyesen magas koleszterin-koncentrációval rendelkeztek-e, mint azok, akik csak két órás TV-t néznek.
az elemzés elvégzéséhez a kutató 100 egészséges férfi résztvevőt vett fel 45-65 éves kor között. Mind a 100 résztvevő esetében rögzítették a tévénézés (azaz a független változó, az idő_tv) és a koleszterin koncentráció (azaz a függő változó, a koleszterin) időtartamát., Változó értelemben kifejezve a kutató a koleszterin időben történő regresszióját akarta.
megjegyzés: az útmutatóhoz használt példa és adatok fiktívek. Most hoztuk létre őket az útmutató céljára.
Stata
Setup in Stata
Megjegyzés: Nem számít, hogy először hozza létre a függő vagy független változót.
e két változó – time_tv és koleszterin-létrehozása után az adatszerkesztő (Szerkesztés) táblázat két oszlopába írtuk be a pontszámokat, az idő , az óra, hogy a résztvevők nézte a TV-t a bal oldali oszlopban (azaz time_tv, a független változó), valamint a résztvevők koleszterin koncentráció mmol/L, a jobb oldali oszlop (azaz, a koleszterin, a függő változó), az alábbiak szerint:
Megjelent írásos engedélye StataCorp LP.,
Stata
vizsgálati eljárás Stata
ebben a szakaszban megmutatjuk, hogyan kell elemezni az adatokat lineáris regresszió Stata amikor a hat feltételezések az előző szakaszban, feltételezések, nem sérülnek. A lineáris regressziót a code vagy a Stata grafikus felhasználói felülete (GUI) segítségével hajthatja végre. Miután elvégezte az elemzést, megmutatjuk, hogyan kell értelmezni az eredményeket. Először válassza ki, hogy használni kívánja-e a code vagy a Stata grafikus felhasználói felületét (GUI).,
Kód
A kód elvégzésére lineáris regresszió az adatok olyan formában:
visszafejlődés DependentVariable IndependentVariable
Ezt a kódot a az alábbi mezőbe:
Megjelent írásos engedélye StataCorp LP.,
példánk segítségével, ahol a függő változó koleszterin, a független változó pedig time_tv, a szükséges kód a következő lenne:
regress koleszterin time_tv
Megjegyzés 1: pontosnak kell lennie, amikor a kódot beírja a mezőbe. A kód “eset érzékeny”. Például, ha beírta a “koleszterin” – t, ahol a” C ” nagybetűs, nem pedig kisbetűs (azaz,, egy kis “c”), amelynek meg kell lennie, hibaüzenetet kap, mint például a következő:
2.Megjegyzés: Ha még mindig a 2. megjegyzés hibaüzenetet kapja: fent érdemes ellenőrizni azt a nevet, amelyet az Adatszerkesztőben megadott a fájl beállításakor (azaz lásd a fenti adatszerkesztő képernyőt)., Az adatszerkesztő képernyő jobb oldalán található mezőben a változókat a
szakaszban írja le, nem pedig a
szakaszban, amelyet be kell írnia a kódba (lásd alább a függő változónkat). Ez nyilvánvalónak tűnhet, de néha hiba történik, ami a fenti 2.megjegyzés hibáját eredményezi.
ezért írja be a kódot, regresszálja a koleszterin time_tv-t, majd nyomja meg a billentyűzeten a” Return/Enter ” gombot.,
megjelent írásbeli engedélyével StataCorp LP.
láthatja az itt előállított Stata kimenetet.,
grafikus felhasználói felület (GUI)
a lineáris regresszió végrehajtásához szükséges három lépés a 12-es és 13-as Statában az alábbiakban látható:
- kattintson a statisztikákra > lineáris modellek és kapcsolódó > lineáris regresszió a főmenüben, az alábbiak szerint:
megjelent írásbeli engedélyével statacorp LP.,
a regresszió – lineáris regressziós párbeszédpanel jelenik meg:
megjelent a StataCorp LP írásbeli engedélyével.
- válassza ki a koleszterint a függő változóból: legördülő doboz, a time_tv pedig a független változók közül: legördülő doboz. A következő képernyő jelenik meg:
megjelent a StataCorp LP írásbeli engedélyével.,
-
kattintson a
gombra. Ez generálja a kimenetet.
Stata
Kimenet a lineáris regressziós elemzés a Stata
Ha az adatok telt el feltételezés #3 (azaz, hogy volt egy lineáris kapcsolat a két változó), #4 (azaz nem voltak kiugró értékek), nagyboldogasszony #5 (azaz, hogy volt függetlenségét megfigyelések), nagyboldogasszony #6 (azaz, az adatok azt mutatták, homoscedasticity) pedig feltételezés, #7 (azaz,, a maradványok (hibák) körülbelül általában eloszlottak), amelyeket korábban a feltételezések szakaszban kifejtettünk, csak a következő lineáris regressziós kimenetet kell értelmezni Stata-ban:
megjelent a StataCorp LP írásbeli engedélyével.,
a kimenet négy fontos információból áll: (a) az R2 érték (“R-négyzet” sor) a függő változóban a variancia arányát jelenti, amely független változónkkal magyarázható (technikailag ez a regressziós modell által elszámolt variáció aránya az átlagos modell felett és azon túl). Az R2 azonban a mintán alapul, és pozitívan elfogult becslés a regressziós modell által elszámolt függő változó varianciájának arányáról (azaz,, túl nagy); B) korrigált R2 érték (“Adj R-négyzet” sor), amely korrigálja a pozitív torzítást, hogy olyan értéket biztosítson, amely a populációban várható; c) az F érték, a szabadság foka (“F (1, 98)”) és a regressziós modell statisztikai jelentősége (“Prob > F” sor); és d) az állandó és független változó (“Coef.”oszlop), amely az információ Meg kell megjósolni a függő változó, koleszterin, a független változó, time_tv.
ebben a példában R2 = 0,151. Korrigált R2 = 0,143 (hogy 3 d. p.,), ami azt jelenti, hogy a független változó, a time_tv magyarázza a függő változó, a koleszterin változékonyságának 14,3% – át a populációban. A korrigált R2 szintén a hatásméret becslése, amely 0, 143 (14, 3%), A Cohen (1988) osztályozása szerint közepes hatásméretre utal. Általában azonban az R2 nem a korrigált R2, amelyet az eredményekben jelentettek. Ebben a példában a regressziós modell statisztikailag szignifikáns, F (1, 98) = 17, 47, p = .0001., Ez azt jelzi, hogy összességében az alkalmazott modell statisztikailag szignifikánsan megjósolhatja a függő változót, a koleszterint.
megjegyzés: a fenti lineáris regressziós elemzésből származó kimenetet mutatjuk be. Mivel azonban meg kellett volna vizsgálnia az adatait a feltételezések szakaszban korábban ismertetett feltételezésekre, akkor is értelmeznie kell a Stata kimenetet, amelyet akkor állítottak elő, amikor ezeket a feltételezéseket tesztelte. Ez magában foglalja: (a) a szórólapok, amelyeket annak ellenőrzésére használt, hogy van-e lineáris kapcsolat a két változó között (azaz, Feltételezés #3); (b) casewise diagnosztika, hogy ellenőrizze, nem voltak kiugró értékek (azaz a Feltételezés #4); (c) a kimenet a Durbin-Watson statisztika, hogy ellenőrizze a függetlenségét megfigyelések (azaz a Feltételezés #5); (d) egy scatterplot a standardizált regressziós maradványok ellen a standardizált regressziós becsült értéket meghatározni, hogy az adatok azt mutatták, homoscedasticity (azaz a Feltételezés #6); valamint egy hisztogram (az egymásra normál görbe) pedig Normál P-P Telek, hogy ellenőrizze, hogy a maradványok (hibák) megközelítőleg normális eloszlású (azaz a Feltételezés #7)., Ne feledje továbbá, hogy ha az adatok ezen feltételezések bármelyikét meghiúsítják, akkor a lineáris regressziós eljárásból származó kimenet (azaz a fent tárgyalt kimenet) már nem lesz releváns, ezért előfordulhat, hogy más statisztikai tesztet kell elvégeznie az adatok elemzéséhez.,
Stata
Adatszolgáltatási a kimenet lineáris regressziós elemzés
Ha a jelentést a kimenet a lineáris regresszió, a helyes gyakorlat az, hogy a következők: (a) bevezetés az elemzés, amit végzett; (b) tájékoztatást arról, hogy a minta, beleértve a hiányzó értékeket; (c) a megfigyelt F-érték szabadságfok, valamint szignifikancia szinten (azaz a p-érték); (d) a százalékos aránya, a változékonyság, a függő változó azzal magyarázható, hogy a független változó (azaz a Korrigált R2 ); valamint (e) a regressziós egyenlet a modell., A fenti eredmények alapján a vizsgálat eredményeit a következőképpen jelenthetjük:
- általános
lineáris regresszió megállapította, hogy a tévénézés napi ideje statisztikailag szignifikánsan előre jelezheti a koleszterin koncentrációját, F(1, 98) = 17, 47, p = .A 0001 és a tévénézés során eltöltött idő a koleszterin koncentrációjának 14,3% – át tette ki. A regressziós egyenlet: előre jelzett koleszterin koncentráció = -2,135 + 0,044 x (tévénézés ideje).,
amellett, hogy a jelentés az eredményeket, mint fent, a diagram lehet használni, hogy vizuálisan bemutatni az eredményeket. Például, meg tudná csinálni ezt egy scatterplot bizalommal és predikciós intervallumok (bár ez nem túl gyakori, hogy adjunk az utolsó). Ez megkönnyítheti mások számára az eredmények megértését. Továbbá használhatja a lineáris regressziós egyenletet, hogy előrejelzéseket készítsen a függő változó értékéről a független változó különböző értékei alapján., Míg a Stata nem állítja elő ezeket az értékeket a fenti lineáris regressziós eljárás részeként, van egy eljárás a Stata-ban, amelyet erre használhat.