feltételezése normalitás a függő változó
a független t-teszt megköveteli, hogy a függő változó körülbelül általában eloszlik az egyes csoportok.
Megjegyzés: technikailag a maradványokat kell általában elosztani, de egy független t-teszthez mindkettő ugyanazt az eredményt adja.,
ezt számos különböző teszt segítségével tesztelheti, de a Shapiro-Wilks normalitás tesztje vagy egy grafikus módszer, például egy Q-Q telek, nagyon gyakori. Ezeket a teszteket SPSS-statisztikák segítségével futtathatja, amelyek eljárása megtalálható a normalitás-útmutató tesztelésében. A T-tesztet azonban a normalitás feltételezése tekintetében robusztus tesztnek írják le. Ez azt jelenti, hogy a normalitástól való eltérés nem befolyásolja nagy mértékben az I. típusú hibaarányt. Ez alól kivételt képez, ha a legkisebb és a legnagyobb csoportméret aránya nagyobb, mint 1.,5 (legnagyobb a legkisebbhez képest).
Mit kell tenni, ha ön megsérti a normális feltételezés
Ha úgy találja, hogy vagy az egyik, vagy mindkét csoport adatai nem közelítőleg normális eloszlású, csoportok méretben különböznek jelentősen, két lehetősége van: (1) át az adatok, így az adatok lesz normális eloszlású (ehhez az SPSS Statisztikai lásd a kézikönyv az Átalakuló Adatok), illetve (2) futtassa a Mann-Whitney U teszt, amely egy non-parametrikus teszt, amely nem igényel az a feltételezés, a normális (a vizsgálatra az SPSS Statisztikai lásd az útmutató, a Mann-Whitney U-Teszt).,
variancia homogenitásának feltételezése
a független t-teszt feltételezi, hogy a mérendő két csoport varianciái egyenlőek a populációban. Ha a varianciák egyenlőtlenek, ez befolyásolhatja az I. típusú hibaarányt. A variancia homogenitásának feltételezését a Levene varianciák egyenlőségének tesztjével lehet tesztelni, amelyet az SPSS statisztikákban állítanak elő a független t-teszt eljárás futtatásakor., Ha az SPSS statisztikákban lefuttatta a Levene variancia egyenlőségének tesztjét, akkor az alábbiakhoz hasonló eredményt kap:

Ez a variancia homogenitására vonatkozó teszt F-statisztikát és jelentőséget (p-érték) biztosít. Elsősorban a szignifikáns értékkel foglalkozunk-ha nagyobb, mint 0, 05 (azaz p > .05), A csoport eltérések lehet kezelni, mint egyenlő. Ha azonban p < 0,05, akkor egyenlőtlen eltérések vannak, és megsértettük a variációk homogenitásának feltételezését.,
Leküzdése megsértése az a feltételezés, a variancia homogenitása
Ha a Levene Teszt az egyenlő Szórások statisztikailag szignifikáns, ami azt jelzi, hogy a csoport szórások egyenlőtlen a lakosság, hogy korrigálja ezt a jogsértést azzal, hogy nem használja az egyesített becslés a hiba kifejezés a t-statisztika, de ehelyett segítségével egy kiigazítás, hogy a szabadságfokot segítségével a Welch-satterthwaite-et módszer., A valóságban valószínűleg soha nem hallottál ezekről a kiigazításokról, mert az SPSS statisztikái elrejtik ezt az információt, és egyszerűen a két lehetőséget “feltételezett egyenlő varianciák” és “nem feltételezett egyenlő eltérések” – ként címkézik anélkül, hogy kifejezetten feltüntetnék az alkalmazott mögöttes teszteket., Azonban látható, hogy a bizonyíték, hogy ezek a tesztek az alábbiak szerint:
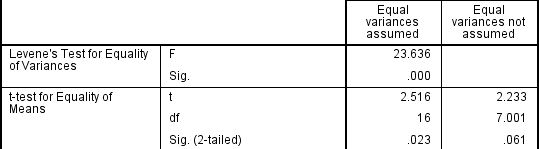
az eredménye Levene-Próba az egyenlő Szórások, tudjuk elutasítja a null hipotézist, hogy nincs különbség a szórások a csoportok között, majd fogadja el az alternatív hipotézist, hogy nincs statisztikailag szignifikáns különbség a szórások a csoportok között., Az a hatás, hogy nem tudunk egyenlő eltéréseket feltételezni, nyilvánvaló a fenti ábra utolsó oszlopában, ahol a T-statisztika értékének csökkenését és a szabadságfok (DF) nagy csökkenését látjuk. Ennek az a hatása, hogy növeli a P-értéket a kritikus szignifikancia szint felett 0,05. Ebben az esetben tehát nem fogadjuk el az alternatív hipotézist, és elfogadjuk, hogy nincs statisztikailag szignifikáns különbség az eszközök között. Ez nem lett volna a következtetésünk, ha nem teszteltük volna a variációk homogenitását.