Mi klasszikusan hiszem, a fény, mint mindig, utazik az egyenes vonalakat, de amikor a fény hullámok hágó közelében, egy akadály hajlamosak könyök körül, hogy akadály válnak szét. A fény diffrakciója akkor fordul elő, amikor egy fényhullám áthalad egy sarkon, vagy egy nyíláson vagy résen keresztül, amely fizikailag a hozzávetőleges mérete, vagy még kisebb, mint a fény hullámhossza.,

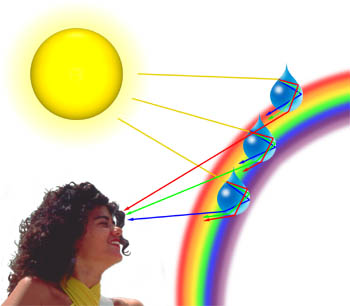
Egy nagyon egyszerű bemutató, fénytörő lehet elvégezni, fogom a kezed előtt egy fényforrás, majd lassan közeledik, két ujjal figyelve, a fény közvetített közöttük. Ahogy az ujjak közelednek egymáshoz, és nagyon közel kerülnek egymáshoz, elkezdesz egy sor sötét vonalat látni az ujjakkal párhuzamosan. A párhuzamos vonalak valójában diffrakciós minták. Ez a jelenség akkor is előfordulhat, ha a fény “meghajlik” olyan részecskék körül, amelyek ugyanolyan nagyságrendűek, mint a fény hullámhossza., Jó példa erre a napfénynek a felhők által történő diffrakciója, amelyet gyakran ezüst bélésnek nevezünk, az 1.ábrán szemléltetve, gyönyörű naplementével az óceán felett.
gyakran megfigyelhetjük a kék, rózsaszín, lila és zöld pasztell árnyalatait olyan felhőkben, amelyek akkor keletkeznek, amikor a felhők vízcseppjeiből diffrakciós fény keletkezik. A diffrakciós mennyiség a fény hullámhosszától függ, a rövidebb hullámhossz nagyobb szögben diffrakciós, mint a hosszabb (valójában a kék és az ibolyaszínű fény nagyobb szögben diffrakciós, mint a vörös fény)., Ahogy a légkörön áthaladó fényhullám egy csepp vízzel találkozik, amint azt az alábbiakban szemléltetjük, először megtörik a vízen:levegő interfész, majd tükröződik, amikor ismét találkozik az interfésszel. A sugár, amely még mindig a vízcsepp belsejében halad, ismét megtörik, mivel harmadik alkalommal ütközik az interfészbe. Ez az utolsó kölcsönhatás az interfésszel visszaveri a fényt a légkörbe, de a fény egy részét is diffrakciója az alábbiakban bemutatott módon., Ez a diffrakciós elem Cellini halo (más néven Heiligenschein-effektus) néven ismert jelenséghez vezet, ahol fényes fénygyűrű veszi körül a megfigyelő fejének árnyékát.
a diffrakciós és szórási kifejezéseket gyakran szinonimaként használják, és szinte szinonimának tekintik. Optikai leírja egy speciális esete a fényszóródás, amelyben egy tárgy a rendszeresen ismétlődő funkciók (például optikai rácsot) termel rendezett fénytörő a fény a diffrakciós kép., A valós világban a legtöbb objektum nagyon összetett alakú, és úgy kell tekinteni, hogy sok egyedi diffrakciós tulajdonságból áll,amelyek együttesen véletlenszerű szórást eredményezhetnek.
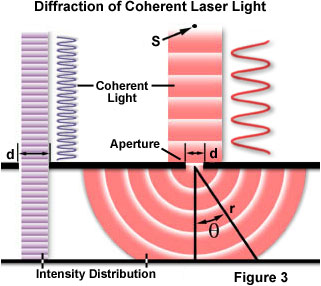
a diffrakcióval járó klasszikus és legalapvetőbb fogalmak egyike az egyrésű optikai diffrakciós kísérlet, amelyet először a tizenkilencedik század elején végeztek. Amikor egy fényhullám egy résen (vagy rekesznyíláson) keresztül terjed, az eredmény a rekesz fizikai méretétől függ az eseménysugár hullámhosszához képest., Ezt a 3.ábra szemlélteti, feltételezve, hogy az S pontból kibocsátott koherens, monokromatikus hullám, hasonlóan a lézerrel előállítható fényhez, áthalad a d nyíláson, és diffrakciós, az elsődleges beeső fénysugár a P pontnál landol, az első másodlagos maxima pedig a Q.
mint az ábra bal oldalán látható, amikor a hullámhossz (λ) sokkal kisebb, mint a rekesznyílás szélessége (D).), A hullám egyszerűen egyenes vonalban halad előre, ugyanúgy, mint ha részecske lenne, vagy nincs nyílás., Ha azonban a hullámhossz meghaladja a rekesz méretét, akkor a fény diffrakcióját a következő egyenlet szerint tapasztaljuk:
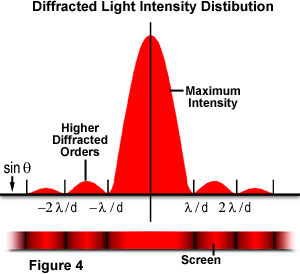
ahol θ az esemény központi terjedési iránya és a diffrakciós minta első minimuma közötti szög. A kísérlet egy fényes központi maximumot hoz létre, amelyet mindkét oldalon másodlagos maximumok szegélyeznek, az egyes egymást követő másodlagos maximumok intenzitása csökken, ahogy a központtól való távolság növekszik. A 4. ábra ezt a pontot szemlélteti a sugár intenzitásának a diffrakciós sugárral szemben., Vegye figyelembe, hogy a másodlagos maximák között előforduló minimumok π többszörösében helyezkednek el.
ezt a kísérletet először Augustin Fresnel magyarázta, aki Thomas Young mellett fontos bizonyítékokat állított elő, amelyek megerősítik, hogy a fény hullámokban halad. A fenti ábrákból láthatjuk, hogy az L pontból kibocsátott koherens, monokromatikus fényt (ebben a példában a lézeres megvilágítást) a D rekesz diffrakciója különbözteti meg., Fresnel feltételezte, hogy az első rend maxima amplitúdóját a Q pontban (eQ-ként definiálva) a következő egyenlet adja meg:
ahol a az eseményhullám amplitúdója, r a D és Q közötti távolság, és f(χ) a χ függvénye, a Fresnel által bevezetett dőléstényező.
fény diffrakciója
fedezze fel, hogyan diffrakciós a fénysugár, amikor áthalad egy keskeny résen vagy nyíláson. Állítsa be a hullámhosszt és a rekesz méretét, és figyelje meg, hogy ez hogyan befolyásolja a diffrakciós intenzitás mintázatát.,
a fény diffrakciója kiemelkedő szerepet játszik bármely optikai eszköz felbontóképességének korlátozásában (például: kamerák, távcsövek, teleszkópok, mikroszkópok és a szem). A felbontóképesség az optikai eszköz azon képessége, hogy két szomszédos pontból különálló képeket készítsen. Ezt gyakran a műszer lencséinek és tükreinek minősége, valamint a környező közeg (általában levegő) tulajdonságai határozzák meg. A fény hullámszerű jellege végső határt szab az összes optikai eszköz felbontóképességének.,
a diffrakciós megbeszéléseink egy rést használtak, mint a nyílást, amelyen keresztül a fény diffrakciós. Azonban minden optikai műszer kör alakú nyílásokkal rendelkezik, például a szem pupillája vagy a körkörös membrán, valamint a mikroszkóp lencséi. A kör alakú nyílások a fent leírtakhoz hasonló diffrakciós mintákat hoznak létre, kivéve, ha a minta természetesen körkörös szimmetriát mutat. A körkörös rekesz által előállított diffrakciós minták matematikai elemzését a következő egyenlet írja le:
ahol θ (1) az elsőrendű diffrakciós minimumok szöghelyzete (az első sötét gyűrű), λ a beeső fény hullámhossza, d A nyílás átmérője, 1,22 pedig állandó. A legtöbb esetben a szög θ(1) nagyon kicsi, így a közelítés, hogy a bűn, s tan a szög majdnem egyenlő hozamok:
ezek az egyenletek nyilvánvalóvá válik, hogy a központi maximális egyenesen arányos λ/d, hogy ez a maximális jobban szét a hosszabb hullámhosszú, valamint a kisebb nyílásokkal., A diffrakció másodlagos mimina korlátozza az objektív lencsék hasznos nagyítását az optikai mikroszkópiában, mivel ezek a lencsék a fény diffrakcióját okozzák. Nem számít, mennyire tökéletes a lencse, a lencse által előállított fényforrás képét másodlagos és magasabb rendű maximák kísérik. Ezt csak akkor lehet kiküszöbölni, ha a lencse végtelen átmérőjű. A θ(1) – nél kisebb távolsággal elválasztott két objektum nem oldható meg, függetlenül attól, hogy mekkora a nagyítás ereje., Míg ezek az egyenletek származtatott a kép egy pont fényforrás végtelen távolságra a rekesz, ez egy ésszerű közelítése felbontóképessége mikroszkóp, amikor d helyett az átmérője az objektív lencse.
Így, ha két tárgy laknak, egy ” D ” távolság választja el egymástól, s a távolból L a megfigyelő, a szög (radiánban kifejezett) között:
ami elvezet minket ahhoz, hogy lecsapódik az utolsó két egyenletek hozam:
ahol D(0) a tárgyak közötti minimális elválasztási távolság, amely lehetővé teszi azok megoldását. Ezzel az egyenletvel az emberi szem képes megoldani a 0,056 milliméter távolsággal elválasztott tárgyakat, azonban a retina fotoreceptorai nem elég közel vannak ahhoz, hogy lehetővé tegyék ezt a felbontási fokot, és a 0,1 milliméter normál körülmények között reálisabb szám.
az optikai mikroszkópok felbontóképességét számos tényező határozza meg, beleértve a tárgyalt tényezőket is, de a legideálisabb körülmények között ez a szám körülbelül 0, 2 mikrométer., Ennek a számnak figyelembe kell vennie a mikroszkóp optikai összehangolását, a lencsék minőségét, valamint a minta ábrázolásához használt fény hullámhosszát. Bár gyakran nem szükséges kiszámítani az egyes célok pontos felbontóképességét (és a legtöbb esetben időpocsékolás lenne), fontos megérteni a mikroszkóp lencsék képességeit, mivel azok a való világra vonatkoznak.
közreműködő szerzők
Mortimer Abramowitz-Olympus America, Inc., Két Vállalati Központ., Melville, New York, 11747.
Michael W., Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.