Ez az első három post sorozat. A harmadik cikk a Big – O formális meghatározásáról szól.
A Big-O jelölés nagyon ijesztő fogalom volt számomra. Arra gondoltam, hogy így beszéltek a” valódi ” programozók a kódjukról. Mindez azért volt ijesztő, mert a tudományos leírások (például a Wikipédia) nagyon kevés értelmet adtak nekem. Ez frusztráló, mert az alulértékeltfogalmak valójában nem olyan nehézek.,
egyszerűen fogalmazva, Big-O jelölés hogyan programozók beszélnialgorithms. Az algoritmusok egy másik ijesztő téma, amelyet be fogok fedniegy másik bejegyzés, de a mi céljainkhoz tegyük fel, hogy az” algoritmus ” azt jelenti, hogy afunction a programban (ami nem túl messze van). A függvény nagy Onotációját az határozza meg, hogy hogyan reagál a különböző bemenetekre. Hogyansokkal lassabb, ha 1000 dolog listáját adjuk meg, amelyen dolgozni kellaz 1 dolog listája helyett?
fontolja meg ezt a kódot:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
tehát ha ezt a funkciót úgy hívjuk, mint a item_in_list(2, ), akkor elég gyorsnak kell lennie., A lista minden egyes elemét átnézzük, és ha megtaláljuk az első érvünket a funkciónkra, akkor visszatérünk a True-ra. Ha elérjük a végetés nem találtuk meg, vissza hamis.
ennek a függvénynek a “bonyolultsága” O(n). Egy pillanat alatt elmagyarázom, hogy ez mit jelent, de bontsuk le ezt a matematikát. O(n)” N”sorrendje olvasható, mert a O függvény szintén rendelési függvényként ismert. Azt hiszem, ez azért van, mert mi csináljukmegközelítés, amely “nagyságrendekkel”foglalkozik.,
a”nagyságrendek” egy újabb matematikai kifejezés, amely alapvetően a számok osztályai közötti különbséget mutatja. Szerintem a különbség 10 és 100 között van. Ha 10 közeli barátodat és 100 embert képzelsz el, az nagy különbség. Hasonlóképpen, az 1000 és 10 000 közötti különbség elég nagy (valójában ez a különbség egy junker autó és egy enyhén használt autó között). Kiderült, hogy a közelítés, amíg te egy nagyságrenddel, te elég közel., Ha kitalálná az amachine-ban lévő gumballok számát, akkor nagyságrendben lenne, ha azt mondaná, hogy 200gumballs. 10,000 gumballs messze lenne.

1.ábra: gumball gép, amelynek gumballjai száma valószínűleg 200 nagyságrendben van.
vissza a dissectingO(n) – hoz, ez azt mondja, hogy ha meg akarjuk ábrázolni az időt, hogy ezt a funkciót különböző méretű bemenetekkel futtassuk (például 1 elem, 2 elem, 3 elem stb.anarray), azt látjuk, hogy ezkörülbelül megfelel a tömb elemeinek számának., Ez egy lineáris gráf. Ez azt jelenti, hogy a vonal alapvetően egyenesha grafizálni kellett volna.
lehet, hogy néhányan észrevették, hogy ha a fenti kódmintában a ouritem mindig a lista első eleme volt, kódunk valóban gyors lenne! Ez igaz, de Big-O szól a hozzávetőleges legrosszabb esetbenteljesítménye csinál valamit. A fenti kód legrosszabb esetehogy a keresett dolog egyáltalán nem szerepel a listán. (Megjegyzés:a matematikai kifejezés erre a “felső határ”, ami azt jelenti, hogy beszél a matematikai határ awfulness).,
ha grafikont szeretne látni ezekhez a függvényekhez, akkor figyelmen kívül hagyja a O() függvényt, és megváltoztatja a n változót x. Ezután írja be ezt azinto Wolfram Alpha-t “plot x” – ként, amely átlósan mutat. Az ok, amiért swap ki N x, hogy a grafikus programwants x, mint a változó neve, mert megfelel a xaxis. Az X-tengely egyre nagyobb balról jobbra megfelel a nagyobb és nagyobb tömbök a függvény., Az y-axis az időt jelenti, így minél magasabb a vonal, annál lassabb.
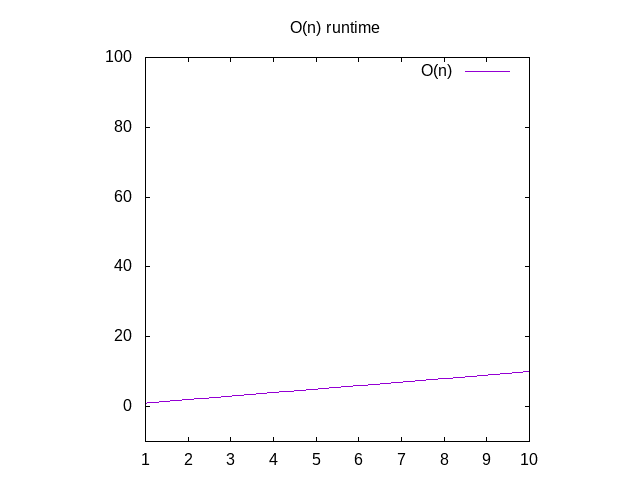
2. ábra: Az O (n) függvény futásidejű jellemzői
tehát mi más példa erre?
fontolja meg ezt a funkciót:
def is_none(item): return item is None
Ez egy kicsit buta példa, de légy velem. Ezt a függvényt O(1) – nek hívják, amelyet “állandó idő” – nek hívnak. Ez azt jelenti, hogy nomatter milyen nagy a bemenetünk, mindig ugyanannyi időt vesz igénybe a dolgok kiszámításához., Ha visszamész a Wolfram-hoz és , látni fogod, hogy mindig ugyanaz marad, függetlenül attól, hogy milyen messzire megyünk. Ha egy 1 millió egész számból álló listán szerepel, akkor nagyjából ugyanannyi időbe telik, mint ha egy 1 egész számból álló listát akarna átadni. Állandó időa függvény legjobb forgatókönyvének tekintik.
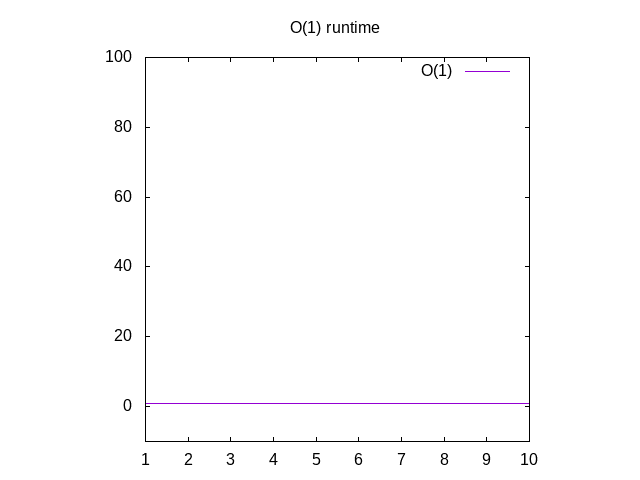
3.ábra: Az O(1) függvény futásidejű jellemzői
fontolja meg ezt a funkciót:
Az alábbiakban összehasonlítjuk az egyes grafikonokat referenciaként., Láthatjuk, hogy egy O(n^2) függvény nagyon gyorsan lelassul, ahol valami, ami állandó időben működik, sokkal jobb lesz. Ez különösen akkor hasznos, amikor az adatstruktúrákról van szó, amelyeket hamarosan közzéteszek.
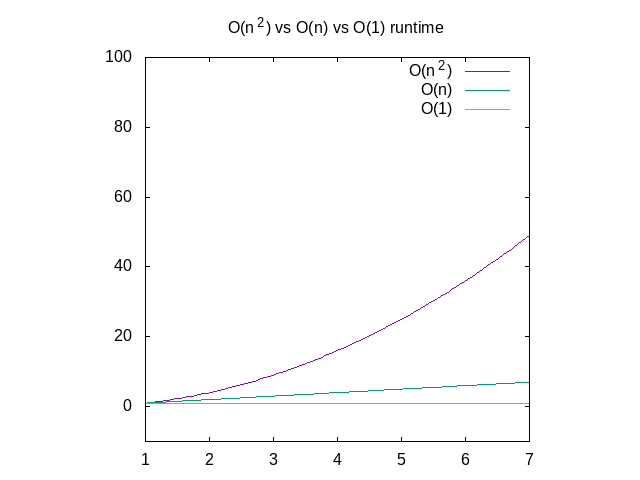
4.ábra: Az O(n2) vs O(n) vs O(1) funkciók összehasonlítása
Ez egy nagyon magas szintű áttekintés A Big-O jelölésről, de reménytelismerkedik a témával., Van egy tanfolyam, amelymeg lehet adni egy alaposabb képet ebben a témában, de figyelmeztetni kell, hogyez ugrik be matematikai jelölés nagyon gyorsan. Ha valami itt nincs értelme, küldjön egy e-mailt.
frissítés: arról is írtam, hogyan kell kiszámítani a Big-O.
arra gondolok, hogy könyvet írok erről a témáról. Ha ez valami, amit látni szeretne, kérjük, fejezze ki érdeklődését itt.