Hypothèse de la normalité de la variable dépendante
Le test t indépendant exige que la variable dépendante soit approximativement normalement distribuée dans chaque groupe.
Remarque: Techniquement, ce sont les résidus qui doivent être normalement distribués, mais pour un test t indépendant, les deux vous donneront le même résultat.,
Vous pouvez tester cela en utilisant un certain nombre de tests différents, mais le test de Shapiro-Wilks de normalité ou une méthode graphique, telle qu’un tracé Q-Q, sont très courants. Vous pouvez exécuter ces tests en utilisant les statistiques SPSS, dont la procédure se trouve dans notre guide Testing for Normality. Cependant, le test t est décrit comme un test robuste en ce qui concerne l’hypothèse de normalité. Cela signifie qu’un certain écart par rapport à la normalité n’a pas une grande influence sur les taux d’erreur de type I. L’exception à cela est si le rapport de la plus petite à la plus grande taille de groupe est supérieur à 1.,5 (le plus grand par rapport au plus petit).
Que faire lorsque vous violez l’hypothèse de normalité
Si vous constatez que l’une ou l’autre des données de votre groupe n’est pas approximativement normalement distribuée et que la taille des groupes diffère considérablement, vous avez deux options: (1) transformez vos données de sorte que les données deviennent normalement distribuées (pour ce faire dans les statistiques SPSS, voir notre guide sur la transformation des données), ou (2) exécutez le test Mann-Whitney U qui est un test non paramétrique qui ne nécessite pas l’hypothèse de normalité (pour exécuter ce test dans les statistiques SPSS, voir notre guide sur la transformation des données).Test de Mann-Whitney U).,
Hypothèse d’homogénéité de la variance
Le test t indépendant suppose que les variances des deux groupes que vous mesurez sont égales dans la population. Si vos variances sont inégales, cela peut affecter le taux d’erreur de type I. L’hypothèse de l’homogénéité de la variance peut être testée à l’aide du test d’égalité des variances de Levene, qui est produit dans les statistiques SPSS lors de l’exécution de la procédure de test t indépendant., Si vous avez exécuté le Test d’Égalité des Variances de Levene dans les statistiques SPSS, vous obtiendrez un résultat similaire à celui ci-dessous:

Ce test d’homogénéité de la variance fournit une statistique F et une valeur de signification (valeur p). Nous sommes principalement concernés par la valeur de signification – si elle est supérieure à 0,05 (c’est-à-dire, p > .05), nos écarts de groupe peuvent être traités comme égaux. Cependant, si p < 0.05, nous avons l’inégalité des variances et nous avons violé l’hypothèse d’homogénéité des variances.,
Surmonter une violation de l’hypothèse d’homogénéité de la variance
Si le test de Levene pour l’égalité des variances est statistiquement significatif, ce qui indique que les variances de groupe sont inégales dans la population, vous pouvez corriger cette violation en n’utilisant pas l’estimation groupée pour le terme d’erreur pour la statistique t, mais en utilisant plutôt un ajustement des degrés de liberté en utilisant la méthode de Welch-Satterthwaite., En réalité, vous n’aurez probablement jamais entendu parler de ces ajustements car les statistiques SPSS masquent ces informations et étiquettent simplement les deux options comme « Variances égales supposées » et « Variances égales non supposées » sans indiquer explicitement les tests sous-jacents utilisés., Cependant, vous pouvez voir la preuve de ces tests comme suit:
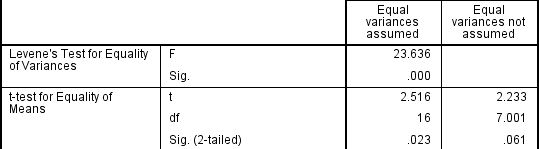
À partir du résultat du test de Levene pour l’égalité des variances, nous pouvons rejeter l’hypothèse nulle selon laquelle il n’y a pas de différence dans les variances entre les groupes et accepter l’hypothèse alternative selon laquelle il existe une différence statistiquement significative dans les variances entre les groupes., L’effet de ne pas pouvoir supposer des variances égales est évident dans la dernière colonne de la figure ci-dessus où nous voyons une réduction de la valeur de la statistique t et une réduction importante des degrés de liberté (df). Cela a pour effet d’augmenter la valeur p au-dessus du niveau de signification critique de 0,05. Dans ce cas, nous n’acceptons donc pas l’hypothèse alternative et acceptons qu’il n’y ait pas de différences statistiquement significatives entre les moyennes. Cela n’aurait pas été notre conclusion si nous n’avions pas testé l’homogénéité des variances.