Support Vector Machine ou SVM est l’un des algorithmes d’apprentissage supervisé les plus populaires, qui est utilisé pour la Classification ainsi que les problèmes de régression. Cependant, il est principalement utilisé pour les problèmes de classification dans l’apprentissage automatique.
L’objectif de l’algorithme SVM est de créer la meilleure ligne ou limite de décision qui puisse séparer l’espace n-dimensionnel en classes afin que nous puissions facilement placer le nouveau point de données dans la catégorie correcte à l’avenir., Cette limite de meilleure décision est appelée un hyperplan.
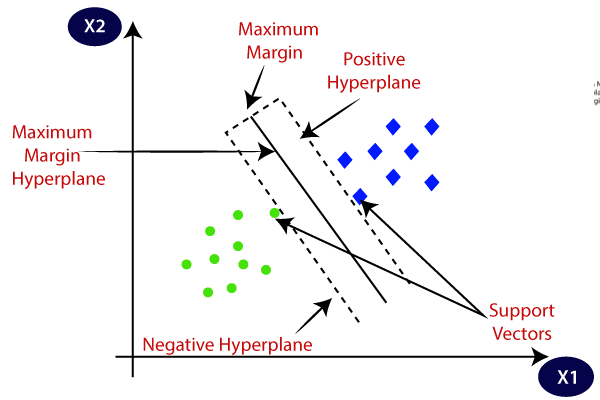
SVM choisit les points / vecteurs extrêmes qui aident à créer l’hyperplan. Ces cas extrêmes sont appelés vecteurs de support, et donc l’algorithme est appelé Machine de vecteur de support. Considérons le diagramme ci-dessous dans lequel il y a deux catégories différentes qui sont classées en utilisant une limite de décision ou un hyperplan:
Exemple: SVM peut être compris avec l’exemple que nous avons utilisé dans le classificateur KNN., Supposons que nous voyons un chat étrange qui a également des caractéristiques de chiens, donc si nous voulons un modèle qui peut identifier avec précision s’il s’agit d’un chat ou d’un chien, un tel modèle peut donc être créé en utilisant l’algorithme SVM. Nous allons d’abord former notre modèle avec beaucoup d’images de chats et de chiens afin qu’il puisse en apprendre davantage sur les différentes caractéristiques des chats et des chiens, puis nous le testons avec cette étrange créature. Ainsi, comme le vecteur de support crée une limite de décision entre ces deux données (chat et chien) et choisit des cas extrêmes (vecteurs de support), il verra le cas extrême de chat et de chien., Sur la base des vecteurs de support, il le classera comme un chat. Considérez le diagramme ci-dessous:
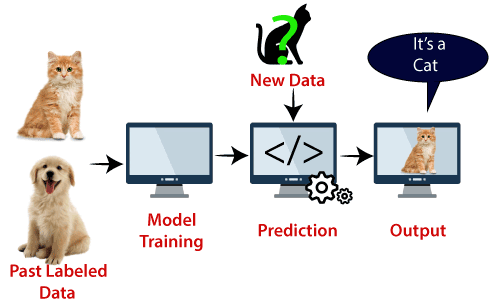
L’algorithme SVM peut être utilisé pour la détection de visage, la classification d’image, la catégorisation de texte, etc.
Types de SVM
SVM peut être de deux types:
- SVM linéaire: Le SVM linéaire est utilisé pour les données séparables linéairement, ce qui signifie que si un ensemble de données peut être classé en deux classes en utilisant une seule ligne droite, ces données sont appelées données séparables linéairement, et le classificateur est,
- SVM non linéaire: SVM non linéaire est utilisé pour les données non séparées linéairement, ce qui signifie que si un ensemble de données ne peut pas être classé en utilisant une ligne droite, ces données sont appelées données non linéaires et le classificateur utilisé est appelé classificateur SVM non linéaire.
Hyperplan et vecteurs de support dans l’algorithme SVM:
Hyperplan: Il peut y avoir plusieurs lignes / limites de décision pour séparer les classes dans l’espace à n dimensions, mais nous devons trouver la meilleure limite de décision qui aide à classer les points de données. Cette meilleure limite est connue sous le nom d’hyperplan de SVM.,
Les dimensions de l’hyperplan dépendent des entités présentes dans l’ensemble de données, ce qui signifie que s’il y a 2 entités (comme indiqué dans l’image), alors l’hyperplan sera une ligne droite. Et s’il y a 3 fonctionnalités, alors hyperplane sera un plan à 2 dimensions.
Nous créons toujours un hyperplan qui a une marge maximale, ce qui signifie la distance maximale entre les points de données.
Vecteurs de support:
Les points de données ou vecteurs les plus proches de l’hyperplan et qui affectent la position de l’hyperplan sont appelés Vecteurs de support., Étant donné que ces vecteurs supportent l’hyperplan, on appelle donc un vecteur de support.
Comment fonctionne SVM?
SVM linéaire:
Le fonctionnement de l’algorithme SVM peut être compris en utilisant un exemple. Supposons que nous ayons un ensemble de données qui a deux balises (vert et bleu), et l’ensemble de données a deux caractéristiques x1 et x2. Nous voulons un classificateur qui peut classer la paire (x1, x2) de coordonnées en vert ou en bleu. Considérez l’image ci-dessous:
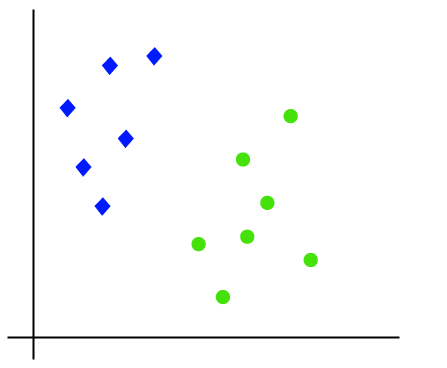
Donc, comme il s’agit d’un espace 2-d, en utilisant simplement une ligne droite, nous pouvons facilement séparer ces deux classes., Mais il peut y avoir plusieurs lignes qui peuvent séparer ces classes. Considérez l’image ci-dessous:
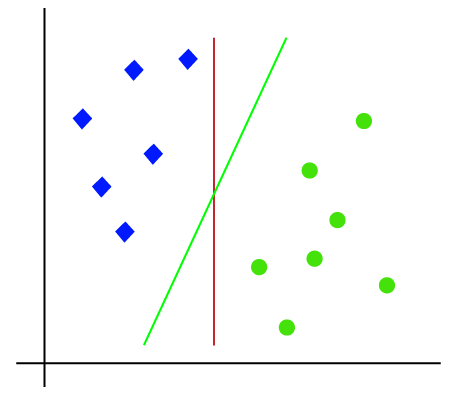
Par conséquent, l’algorithme SVM aide à trouver la meilleure ligne ou la meilleure limite de décision; cette meilleure limite ou région est appelée comme un hyperplan. L’algorithme SVM trouve le point le plus proche des lignes des deux classes. Ces points sont appelés vecteurs de support. La distance entre les vecteurs et l’hyperplan est appelée marge. Et l’objectif de SVM est de maximiser cette marge. L’hyperplan avec une marge maximale est appelé l’hyperplan optimal.,
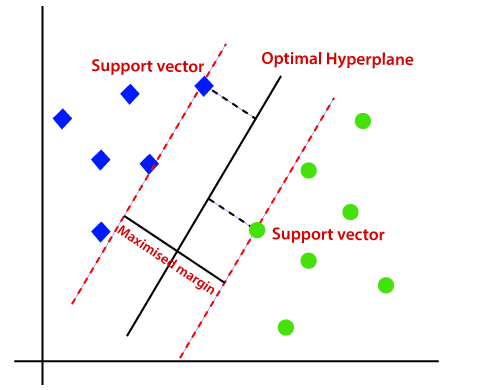
SVM non linéaire:
Si les données sont disposées linéairement, nous pouvons les séparer en utilisant une ligne droite, mais pour les données non linéaires, nous ne pouvons pas tracer une seule ligne droite. Considérez l’image ci-dessous:
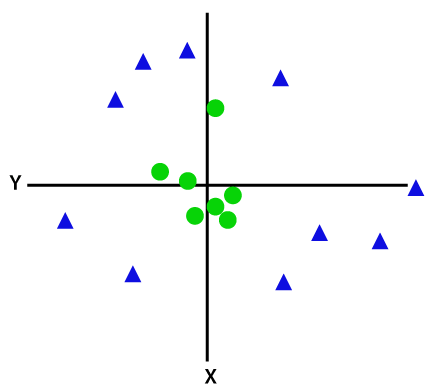
Donc, pour séparer ces points de données, nous devons ajouter une dimension supplémentaire. Pour les données linéaires, nous avons utilisé deux dimensions x et y, donc pour les données non linéaires, nous ajouterons une troisième dimension z., Il peut être calculé comme suit:
z=x2 +y2
En ajoutant la troisième dimension, l’espace d’échantillon deviendra l’image ci-dessous:
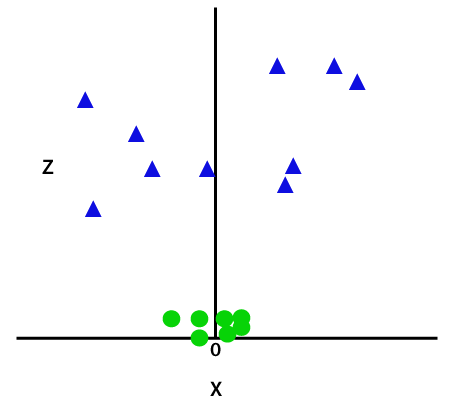
Alors maintenant, SVM divisera les ensembles de données en classes de la manière suivante. Considérez l’image ci-dessous:
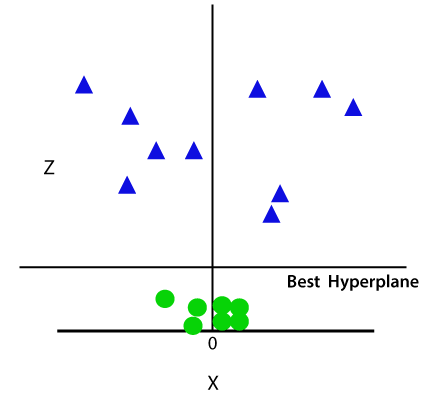
Puisque nous sommes dans l’espace 3d, il ressemble donc à un plan parallèle à l’axe des x. Si nous le convertissons en espace 2d avec z=1, alors il deviendra:
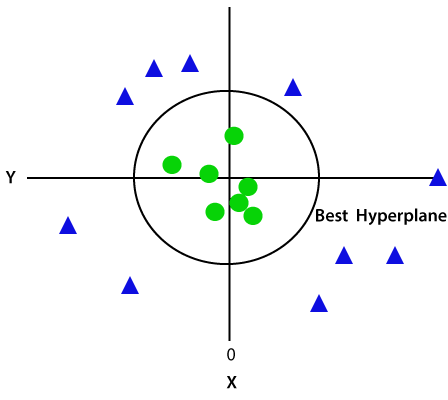
Par conséquent, nous obtenons une circonférence de rayon 1 en cas de données non linéaires.,
Implémentation Python de Support Vector Machine
Maintenant, nous allons implémenter l’algorithme SVM en utilisant Python. Ici, nous utiliserons le même ensemble de données user_data, que nous avons utilisé dans la régression logistique et la classification KNN.
- Étape de prétraitement des données
Jusqu’à l’étape de prétraitement des données, le code restera le même. Voici le code:
Après avoir exécuté le code ci-dessus, nous prétraiterons les données., Le code va donner le jeu de données:
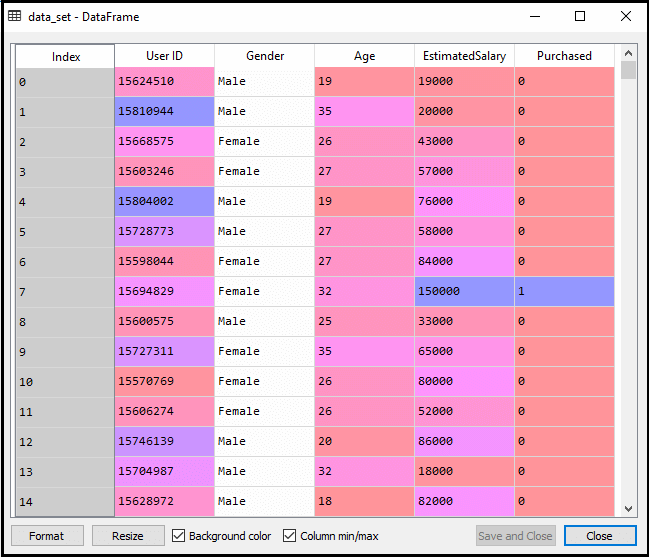
de L’échelle de sortie pour le jeu de test sera:
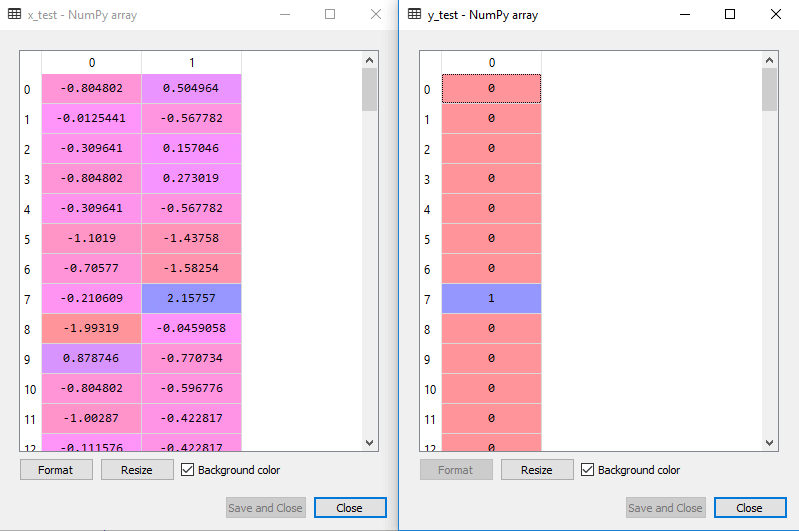
Montage de la SVM pour l’ensemble de la formation:
Maintenant, l’ensemble de la formation sera adaptée à la SVM. Pour créer le classificateur SVM, nous importerons la classe SVC de Sklearn.svm de la bibliothèque. Voici le code pour cela:
Dans le code ci-dessus, nous avons utilisé kernel=’linear’, car ici nous créons SVM pour des données linéairement séparables. Cependant, nous pouvons le changer pour les données non linéaires., Et puis nous avons ajusté le classificateur à l’ensemble de données d’entraînement(x_train, y_train)
Sortie:
Les performances du modèle peuvent être modifiées en changeant la valeur de C (facteur de régularisation), gamma et noyau.
- Prédire le résultat de l’ensemble de test:
Maintenant, nous allons prédire la sortie pour l’ensemble de test. Pour cela, nous allons créer un nouveau vecteur y_pred. Voici le code pour cela:
Après avoir obtenu le vecteur y_pred, nous pouvons comparer le résultat de y_pred et y_test pour vérifier la différence entre la valeur réelle et la valeur prédite.,
Sortie: Voici la sortie pour la prédiction de l’ensemble de tests:

- Création de la matrice de confusion:
Maintenant, nous allons voir les performances du classificateur SVM que combien de prédictions incorrectes sont là par rapport au classificateur de régression logistique. Pour créer la matrice de confusion, nous devons importer la fonction confusion_matrix de la bibliothèque sklearn. Après avoir importé la fonction, nous l’appellerons en utilisant une nouvelle variable cm. La fonction prend deux paramètres, principalement y_true (les valeurs réelles) et y_pred (la valeur ciblée renvoyée par le classificateur)., Voici le code pour cela:
Sortie:
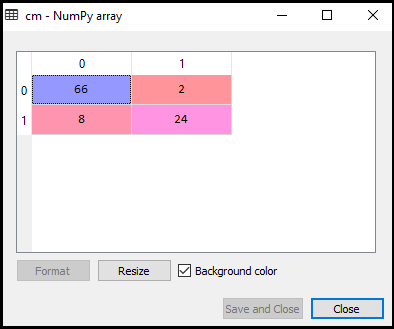
Comme nous pouvons le voir dans l’image de sortie ci-dessus, il y a 66+24= 90 prédictions correctes et 8+2= 10 prédictions correctes. Par conséquent, nous pouvons dire que notre modèle SVM s’est amélioré par rapport au modèle de régression logistique.,
- la Visualisation de l’ensemble de la formation résultat:
Maintenant, nous allons visualiser l’ensemble de la formation résultat, voici le code:
Résultat:
En exécutant le code ci-dessus, nous obtenons le résultat sous la forme:
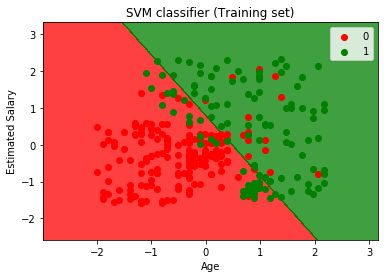
Comme on peut le voir, au-dessus de la sortie est d’apparence similaire à la régression Logistique de sortie. Dans la sortie, nous avons obtenu la ligne droite comme hyperplane parce que nous avons utilisé un noyau linéaire dans le classificateur. Et nous avons également discuté ci-dessus que pour l’espace 2d, l’hyperplan dans SVM est une ligne droite.,
- Visualisation du résultat de l’ensemble de tests:
Sortie:
En exécutant le code ci-dessus, nous obtiendrons la sortie comme:
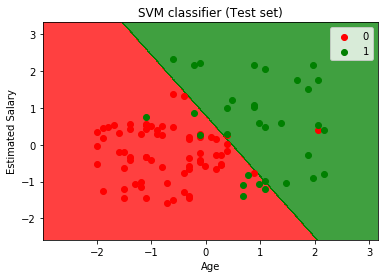
Comme nous pouvons le voir dans l’image de sortie ci-dessus, le classificateur SVM a divisé les utilisateurs en deux régions (achetées ou non achetées). Les utilisateurs qui ont acheté le SUV sont dans la région rouge avec les points de dispersion rouges. Et les utilisateurs qui n’ont pas acheté le SUV sont dans la région verte avec des points de dispersion verts. L’hyperplan a divisé les deux classes en variable achetée et non achetée.