C’est la première d’une série de trois articles. Le deuxième article parle decomment calculer Big-O. Le troisième article parle de comprendre la définition formelle de Big-O.
La notation Big-O était un concept vraiment effrayant pour moi. Je pensais que c’est ainsi que les « vrais » programmeurs ont parlé de leur code. C’était d’autant plus effrayant que les descriptions académiques (telles que Wikipedia) me faisaient très peu de sens. C’est frustrant parce que les concepts sous-jacents ne sont pas vraiment difficiles.,
En termes simples, la notation Big-O est la façon dont les programmeurs parlent d’algorithmes. Les algorithmes sont un autre sujet effrayant que je couvrirai dansun autre article, mais pour nos besoins, disons que « algorithme » signifie une fonction dans votre programme (qui n’est pas trop loin). La Big-Onotation d’une fonction est déterminée par la façon dont elle répond à différentes entrées. Comment est-ce plus lent si nous lui donnons une liste de 1000 choses à travailler au lieu d’une liste de 1 chose?
de Considérer ce code:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Donc, si nous appelons cette fonction comme item_in_list(2, ), il doit être assez rapide., Nous bouclons chaque chose de la liste et si nous trouvonsle premier argument de notre fonction, renvoie True. Si nous arrivons à la finet nous ne l’avons pas trouvé, retournez False.
La « complexité » de cette fonction est: O(n). Je vais expliquer ce que cettesignifie en une seconde, mais décomposons cette syntaxe mathématique. O(n) est lu « Order of N » car la fonction O est également connue comme la fonction Order. Je pense que c’est parce que nous faitapproximation, qui traite des « ordres de grandeur ».,
« Ordres de grandeur » est ENCORE UN AUTRE terme mathématique qui indique essentiellement la différence entre les classes de nombres. Pensez à la différence entre 10 et 100. Si vous imaginez 10 de vos amis les plus proches et 100 personnes, c’est une très grande différence. De même, la différence entre 1 000 et 10 000 est assez grande (en fait, c’est la différence entre une voiture junker et une voiture légèrement utilisée). Il s’avère qu’en approximation, tant que vous êtes dans un ordre de grandeur,vous êtes assez proche., Si vous deviez deviner le nombre de gumballs dans amachine, vous seriez dans un ordre de grandeur si vous disiez 200gumballs. 10 000 gumballs seraient loin.

la Figure 1: Un gumball machine dont le numéro de gumballs est probablement dans un ordre de grandeur de 200.
Retour à la dissection deO(n), cela dit que si nous devions représenter graphiquement le temps nécessaire pour exécuter cette fonction avec des entrées de taille différente (par exemple anarray de 1 élément, 2 éléments, 3 éléments, etc.), nous verrions qu’il correspond approximativement au nombre d’éléments dans le tableau., Cette iscalled un graphique linéaire. Cela signifie que la ligne est fondamentalement droitesi vous deviez la représenter graphiquement.
Certains d’entre vous ont peut-être compris que si, dans l’exemple de code ci-dessus, ouritem était toujours le premier élément de la liste, notre code serait vraiment rapide! C’est vrai, mais Big-O est tout au sujet de la pire performance approximative de faire quelque chose. Le pire des cas pour le code ci-dessus estque la chose que nous recherchons n’est pas du tout dans la liste. (Remarque: Le terme mathématique pour cela est « limite supérieure », ce qui signifie qu’il parle de la limite mathématique de l’awfulness).,
Si vous voulais voir un graphique de ces fonctions, vous ignorez le O()fonction et modifier la variable n par x. Vous pouvez ensuite taper thatinto Wolfram Alpha comme « plot x »qui vous montrera une diagonale. La raison pour laquelle vous échangez n contre x est que leur programme de graphiquewants x comme nom de variable car il correspond à xaxis. L’axe des abscisses qui s’agrandit de gauche à droite correspond àdonner des tableaux de plus en plus grands à votre fonction., L’axe y représente le temps, donc plus la ligne est haute, plus elle est lente.
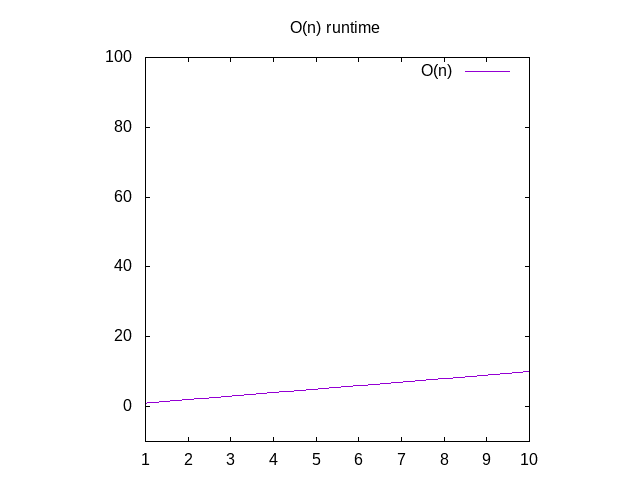
la Figure 2: le temps d’Exécution caractéristiques d’un O(n) la fonction
Alors, quelles sont quelques autres exemples?
prenons cette fonction:
def is_none(item): return item is None
C’est un peu un exemple stupide, mais garder avec moi. Cette fonction est appelée O(1) qui est appelée »temps constant ». Ce que cela signifie, c’est la taille de notre entrée, cela prend toujours le même temps pour calculer les choses., Si vous revenez à Wolfram et plot 1, vous verrez qu’il reste toujours le même, peu importe à quel point nous allons à droite. Si vous passez dans une liste de 1 million d’entiers, cela prendra à peu près le même temps que si vous alliez passer dans une liste de 1 entier. Le temps constant est considéré comme le meilleur scénario pour une fonction.
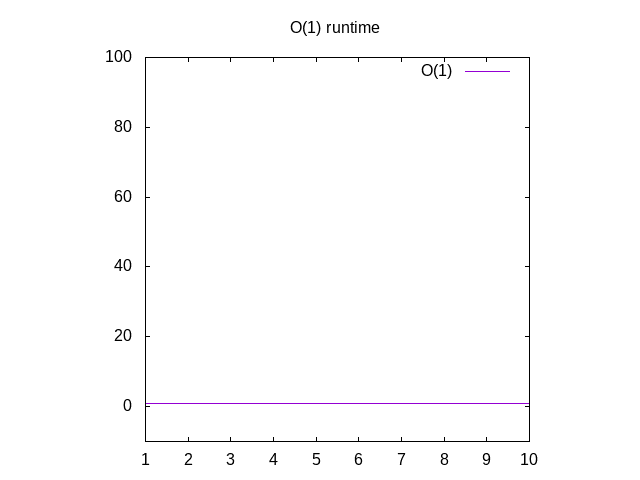
Figure 3: Exécution caractéristiques d’un O(1) de la fonction
prenons cette fonction:
ci-Dessous une comparaison de chacun de ces graphiques, pour référence., Vous pouvez voir qu’une fonction O(n^2) sera lente très rapidement où quelque chose qui fonctionne en temps constant sera beaucoup mieux. Ceci est particulièrement utile en ce qui concerne les structures de données, que je publierai bientôt.
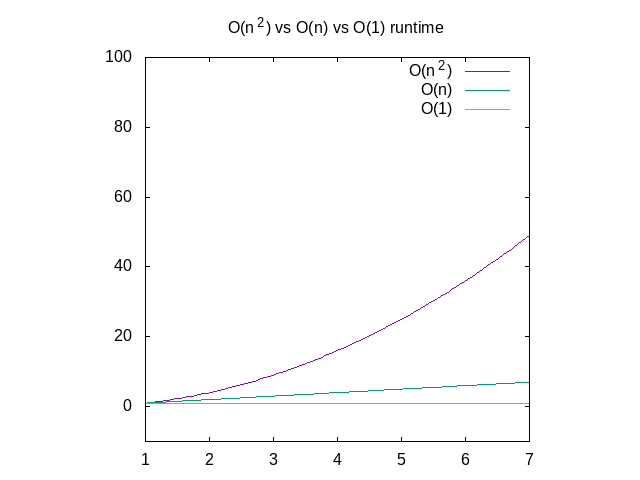
Figure 4: Comparaison des fonctions O(n2) vs O(n) vs O(1)
Ceci est un aperçu assez élevé de la notation Big-O, mais espérons que vous vous familiariserez avec le sujet., Il y a un cours coursera qui peut vous donner une vue plus approfondie de ce sujet, mais soyez averti qu’il va sauter dans la notation mathématique très rapidement. Si quelque chose ici n’a pas de sens, envoyez-moi un e-mail.
Mise à jour: J’ai également écrit sur la façon de calculer Big-O.
Je pense à écrire un livre sur ce sujet. Si c’est quelque chose que vous aimeriez voir, veuillez exprimer votre intérêt ici.