la Variance de déterminer dans quelle mesure un ensemble de données réparties. Une variance de zéro indique que toutes les valeurs des données sont identiques. Toutes les variances non nulles sont positives.

Une petite variance indique que les points de données ont tendance à être très proches de la moyenne, et les uns des autres., Une variance élevée indique que les points de données sont très répartis par rapport à la moyenne et les uns des autres. La variance est la moyenne des distances au carré entre chaque point et la moyenne.

Le processus de recherche de la variance est très similaire à la recherche de la déviation absolue moyenne.
La seule différence est la quadrature des distances.
Processus: (1) Trouver la moyenne de l’ensemble. (2) Soustrayez chaque valeur de données de la moyenne pour trouver sa distance par rapport à la moyenne. (3) Carré toutes les distances. (4) Ajouter tous les carrés des distances., (4) Diviser par le nombre de données (pour la variance de la population).

Un problème avec la variance, c’est qu’il n’a pas la même unité de mesure que les données d’origine. Par exemple, les données originales contenant des longueurs mesurées en pieds ont une variance mesurée en pieds carrés.,

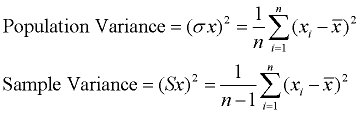Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Si vous calculez à la main, reportez toujours plus de décimales dans les calculs que prévu pour le résultat final. Si vous travaillez avec une calculatrice, reportez la valeur complète des entrées de la calculatrice jusqu’à ce que vous arriviez au résultat final.

écart-type montre comment le degré de variation (dispersion, diffusion, dispersion) à partir de la moyenne existe., Il représente un écart » typique  » par rapport à la moyenne. C’est une mesure populaire de la variabilité car elle revient aux unités de mesure d’origine de l’ensemble de données.

Un faible écart-type indique que les points de données ont tendance à être très proches de la moyenne. Un écart type élevé indique que les points de données sont répartis sur une large plage de valeurs.
L’écart type peut être considéré comme un moyen » standard  » de savoir ce qui est normal (typique), ce qui est très grand et ce qui est très petit dans l’ensemble de données.,

L’écart-type est une mesure populaire de la variabilité car il revient aux unités de mesure d’origine de l’ensemble de données. Par exemple, les données originales contenant des longueurs mesurées en pieds ont un écart type également mesuré en pieds.,

Pour calculer l’écart type à la main:
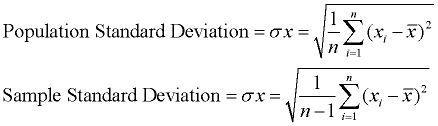L’écart-type est tout simplement la racine carrée de la variance.
Cette description sert à calculer l’écart type de la population. Si l’écart type de l’échantillon est nécessaire, diviser par n – 1 au lieu de n., Depuis l’écart-type est la racine carrée de la variance, nous devons d’abord calculer la variance.
1. Trouver la moyenne.
2. Soustrayez la moyenne de chaque valeur de données et mettez au carré chacune de ces différences (les différences au carré).
3. Trouvez la moyenne des différences au carré (ajoutez-les et divisez-les par le nombre de valeurs de données). Ce sera la variance.,

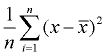écart
4. Prendre la racine carrée. Ce sera l’écart type de la population. Arrondissez la réponse selon les instructions du problème.

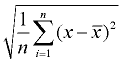écart-type

La Courbe normale

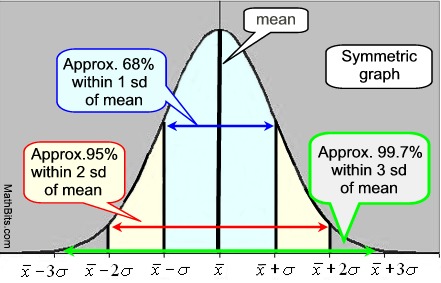
Une courbe normale est symétrique, en forme de cloche de la courbe., Le centre du graphe est la moyenne, et la hauteur et la largeur du graphique est déterminé par l’écart-type. Lorsque l’écart type est faible, la courbe sera haute et étroite. Lorsque l’écart type est important, la courbe sera courte et large. La moyenne et la médiane ont la même valeur dans une courbe normale.

Courbe Normale Règle Empirique:
Environ …

• 68% des données se trouvent dans un écart-type de la moyenne.,

• 95% des données se trouvent dans deux écarts-types de la moyenne.

• 99,7% des données se trouvent dans trois écarts-types de la moyenne.

IQR pour une courbe normale est de 1,34896 x écart type.