FRANK K. MCKINNEY

L’ÂGE des fossiles intrigue presque tout le monde. Les étudiants veulent non seulement savoir quel âge a un fossile, mais ils veulent savoir comment cet âge a été déterminé. Certains principes très simples sont utilisés pour déterminer l’âge des fossiles. Les étudiants devraient être capables de comprendre les principes et d’avoir cela comme arrière-plan afin que les déterminations d’âge par les paléontologues et les géologues ne semblent pas être de la magie noire.

Il existe deux types de détermination de l’âge., Les géologues de la fin du 18e et du début du 19e siècle ont étudié les couches rocheuses et les fossiles pour déterminer l’âge relatif. William Smith était l’un des scientifiques les plus importants de cette époque qui a aidé à développer la connaissance de la succession des différents fossiles en étudiant leur distribution à travers la séquence des roches sédimentaires dans le sud de l’Angleterre. Ce n « est que bien au 20e siècle que suffisamment d « informations s » étaient accumulées sur le taux de désintégration radioactive pour que l « âge des roches et des fossiles en nombre d » années puisse être déterminé par âge radiométrique sortir ensemble.,

Cette activité sur la détermination de l’âge des roches et des fossiles est destinée aux élèves de 8e ou 9e année. On estime qu’il faut quatre heures de cours, dont environ une heure d’enseignement et d’explication occasionnels de la part de l’enseignant et deux heures d’activités en groupe (en équipe) et individuelles par les élèves, plus une heure de discussion entre les élèves au sein des groupes de travail.,

Explorez ce lien pour plus d’informations sur les sujets abordés dans cette leçon:

  • Temps géologique

BUT ET OBJECTIFS

Cette activité aidera les élèves à mieux comprendre les principes de base utilisés pour déterminer l’âge des roches et des fossiles. Cette activité se compose de plusieurs parties. Les objectifs de cette activité sont les suivants:
1) Demander aux élèves de déterminer l’âge relatif d’une zone géologiquement complexe.
2) Familiariser les élèves avec le concept de demi-vie dans la désintégration radioactive.,
3) Pour que les étudiants voient que les exécutions individuelles de processus statistiques sont moins prévisibles que la moyenne de nombreuses exécutions (ou que les exécutions avec des nombres relativement petits impliqués sont moins fiables que les exécutions avec de nombreux nombres).
4) Pour démontrer comment le taux de désintégration radioactive et l’accumulation du produit de désintégration résultant est utilisé dans la datation radiométrique des roches.

5) Utiliser la datation radiométrique et les principes de détermination de l « âge relatif pour montrer comment les âges des roches et des fossiles peuvent être rétrécis même s » ils ne peuvent pas être datés radiométriquement.,
Retour en haut

MATÉRIAUX REQUIS POUR CHAQUE GROUPE

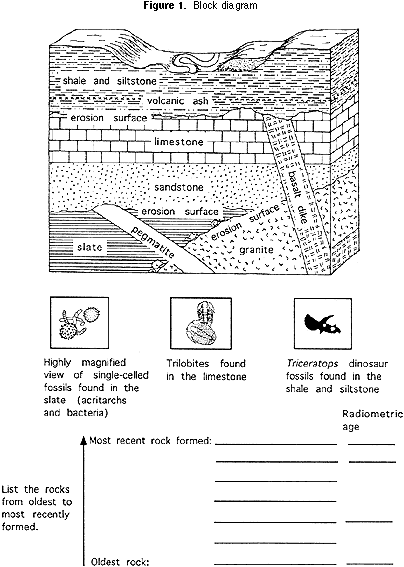
1) Schéma fonctionnel (Figure 1).
2) Grande tasse ou autre récipient dans lequel M & M peut être ébranlé.
3) 100 M & M
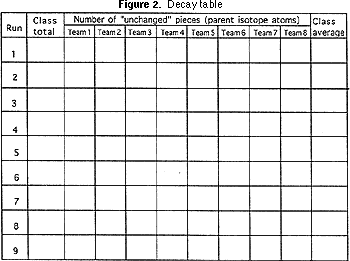
4) papier millimétré (Figure 2).
5) Montre ou horloge qui garde le temps en secondes. (Une seule montre ou horloge pour toute la classe fera l’affaire.)
6) Morceau de papier marqué TEMPS et indiquant soit 2, 4, 6, 8, ou 10 minutes.,
7) 128 petites cartes ou boutons qui peuvent être découpés dans du carton ou du papier de construction, de préférence avec une couleur différente sur les côtés opposés, chacun marqué avec « U-235 » tous sur un côté coloré et « Pb-207 » sur le côté opposé qui a une certaine couleur contrastante.,



Retour

PARTIE 1: DÉTERMINER l’ÂGE RELATIF DES ROCHES

Chaque équipe de 3 à 5 élèves devraient discuter ensemble de la façon de déterminer l’âge relatif de chacune des unités rocheuses dans le diagramme (Figure 1). Une fois que les élèves ont décidé comment établir l’âge relatif de chaque unité de roche, ils devraient les énumérer sous le bloc, du plus récent en haut de la liste au plus ancien en bas.,

L’enseignant doit dire aux élèves qu’il existe deux principes de base utilisés par les géologues pour déterminer la séquence des âges des roches. Ils sont:
Principe de superposition: Des roches sédimentaires plus jeunes sont déposées sur des roches sédimentaires plus anciennes.
Principe des relations transversales: Toute caractéristique géologique est plus jeune que toute autre chose qu’elle traverse.

PARTIE 2: DATATION PAR ÂGE RADIOMÉTRIQUE

Certains éléments ont des formes (appelées isotopes) avec des noyaux atomiques instables qui ont tendance à changer ou à se désintégrer., Par exemple, U-235 est un isotope instable deuranium qui a 92 protons et 143 neutrons dans le noyau de chaque atome. Grâce à une série de changements dans le noyau, il émet plusieurs particules, se terminant par 82 protons et 125 neutrons. C’est une condition stable, et il n’y apas plus de changements dans le noyau atomique. Un noyau avec ce nombre de protonsest appelé plomb (symbole chimique Pb). Les protons (82) et les neutrons (125) totalisent 207. Cette forme particulière (isotope) du plomb est appelée Pb-207. U-235 est le parentisotope de Pb-207, qui est l’isotope fille.,

De nombreuses roches contiennent de petites quantités d’isotopes instables et les isotopes filles dans lesquels elles se désintègrent. Lorsque les quantités d’isotopes parents et filles peuvent être mesurées avec précision, le rapport peut être utilisé pour déterminer l’âge de la roche, comme indiqué dans les activités suivantes.

Partie 2a Activité-À tout moment, il y a une petite chance que chacun des noyaux de U-235 se désintègre soudainement. Cette chance de décomposition est très faible, mais elle est toujours présente et ne change jamais. En d’autres termes, les noyaux ne « s’usent » ni ne se « fatiguent »., Si le noyau ne s’est pas encore décomposé, il y a toujours la même, légère chance qu’il change dans un proche avenir.

Les noyaux atomiques sont maintenus ensemble par une attraction entre les grosses particules nucléaires (protons et neutrons) connue sous le nom de « force nucléaire forte », qui doit dépasser la répulsion électrostatique entre les protons dans le noyau., En général, à l’exception du proton unique qui constitue le noyau de l’isotope le plus abondant de l’hydrogène, le nombre de neutrons doit au moins être égal au nombre de protons dans un noyau atomique, car la répulsion électrostatique interdit l’emballage plus dense des protons. Mais s’il y a trop de neutrons, le noyau est potentiellement instable et la désintégration peut être déclenchée. Cela se produit à tout moment lorsque l’addition de la « force nucléaire faible » fugace à la répulsion électrostatique toujours présente dépasse l’énergie de liaison requise pour maintenir le noyau ensemble.,

Des mesures très minutieuses en laboratoire, effectuées sur un TRÈS grand nombre d’atomes U-235, ont montré que chacun des atomes a une chance 50:50 de se désintégrer pendant environ 704 000 000 d’années. En d’autres termes, pendant 704 millions d’années, la moitié des atomes U-235 qui existaient au début de cette période se désintégreront en Pb-207. Ceci est connu comme la demi-vie de U-235. De nombreux éléments ont des isotopes instables, essentiellement parce qu’ils ont trop de neutrons pour être équilibrés par le nombre de protons dans le noyau. Chacun de ces isotopes instables a sa propre demi-vie caractéristique., Certains demi-vie de plusieurs milliards d’années, et d’autres sont aussi courtes qu’un dix-millième de seconde.
Retour en haut

Une façon savoureuse pour les étudiants de comprendre la demi-vie est de donner à chaque équipe 100 morceaux de « régulier » M& M bonbons. Sur un morceau de papier pour ordinateur portable, chaque morceau doit être placé avec le M imprimé vers le bas. Cela représente l’isotope parent., Les bonbons doivent être versés dans un récipient assez grand pour qu’ils rebondissent librement, ils doivent être bien agités, puis versés sur le papier pour qu’il soit étalé au lieu de faire une pile. Cette première fois de secousse représente une demi-vie, et tous ces morceaux de bonbons qui ont le M imprimé vers le haut représentent un changement à l’isotope fille. L’équipe doit ramasser et mettre de côté UNIQUEMENT les morceaux de bonbons qui ont le M vers le haut. Ensuite, comptez le nombre de morceaux de bonbons restants avec le M vers le bas., Ce sont les isotopes parents qui n’ont pas changé pendant la première demi-vie.

L’enseignant devrait demander à chaque équipe de signaler le nombre de morceaux d’isotope parent restant, et la première ligne du tableau de désintégration (Figure 2) devrait être remplie et le nombre moyen calculé. La même procédure de secousse, de comptage des « survivants » et de remplissage de la rangée suivante sur la table de désintégration devrait être effectuée sept ou huit fois de plus. Chaque fois représente une moitié de la vie.

Une fois les résultats de la « demi-vie » finale du M& M collectés, les bonbons ne sont plus nécessaires.,

Chaque équipe doit tracer sur un graphique (Figure 3) le nombre de morceaux de bonbons restant après chacun de leurs « shakes » et connecter chaque point successif sur le graphique avec une ligne de lumière. Sur le même graphique, chaque équipe doit tracer les VALEURS MOYENNES de la classe dans son ensemble et les relier par une ligne plus lourde. ET, sur le même graphique, chaque groupe doit tracer des points où, après chaque « secousse », le nombre de départ est divisé par exactement deux et relier ces points par une ligne de couleur différente. (Cette ligne commence à 100; le point suivant est de 100/ 2, ou 50, le point suivant est 50/2, ou 25, et ainsi de suite.,

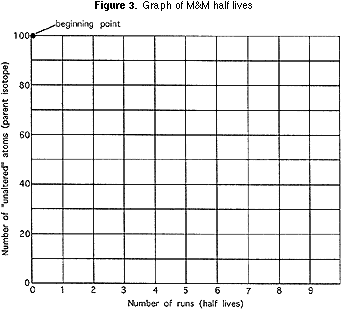Une fois les graphiques tracés, l’enseignant doit guider la classe dans sa réflexion sur:
1) Pourquoi chaque groupe n’a-t-il pas obtenu les mêmes résultats?
2) Qui suit mieux la ligne mathématiquement calculée? Est-ce les résultats du groupe unique, ou est-ce la ligne basée sur la moyenne de classe? Pourquoi?
3) Les élèves ont-ils eu plus de facilité à deviner (prédire) les résultats quand il y avait beaucoup de morceaux de bonbons dans la tasse, ou quand il y en avait très peu? Pourquoi?

U-235 se trouve dans la plupart des roches ignées., À moins que la roche ne soit chauffée à une température très élevée, l’U-235 et sa fille Pb-207 restent dans la roche. Un géologue peut comparer la proportion d’atomes U-235 à Pb-207 produits à partir de celui-ci et déterminer l’âge de la roche. La partie suivante de cet exercice montre comment cela se fait.
Retour en haut

Partie 2b Activité — Chaque équipe reçoit 128 pièces plates, avec U-235 écrit d’un côté et Pb-207 écrit de l’autre côté. Chaque équipe reçoit un morceau de papier marqué TIME, sur lequel est écrit soit 2, 4, 6, 8, ou 10 minutes.,

L’équipe doit placer chaque pièce marquée de sorte que « U-235 » s’affiche. Cela représente l’Uranium-235, qui émet une série de particules du noyau lorsqu’il se désintègre en plomb-207 (Pb-207). Lorsque chaque équipe est prête avec les 128 pièces montrant toutes « U-235 », un intervalle chronométré de deux minutes devrait commencer. Pendant ce temps, chaque équipe retourne plus de la moitié des pièces U-235 de sorte qu’ils montrent maintenant Pb-207. Cela représente une « demi-vie » de U-235, qui est le temps pour la moitié des noyaux de passer du parent U-235 à la fille Pb-207.

Un nouvel intervalle de deux minutes commence., Pendant ce temps, l’équipe devrait retourner LA MOITIÉ DU U-235 QUI A ÉTÉ LAISSÉ APRÈS LE PREMIER INTERVALLE DE TEMPS. Continuez à travers un total de 4 à 5 intervalles chronométrés.

Cependant, chaque équipe doit CESSER de retourner les pièces à l’heure indiquée sur ses papiers de TEMPS. C’est-à-dire que chaque équipe doit s’arrêter en fonction de son calendrier à la fin du premier intervalle chronométré (2 minutes), ou à la fin du deuxième intervalle chronométré (4 minutes), etc. Une fois que tous les intervalles chronométrés ont eu lieu, les équipes doivent échanger des places entre elles selon les instructions de l’enseignant., La tâche maintenant pour chaque équipe est de déterminer combien d’intervalles chronométrés (c’est-à-dire combien de demi-vies) l’ensemble des pièces qu’ils regardent a connu.

La demi-vie d’U-235 est de 704 millions d’années. L’équipe qui a retourné un ensemble de pièces et la deuxième équipe qui a examiné l’ensemble devraient déterminer combien de millions d’années sont représentées par la proportion de U-235 et Pb-207 présents, comparer les notes et marchander sur les différences qu’ils ont obtenues., (À droite, chaque équipe doit déterminer le nombre de millions d’années représentées par l’ensemble qu’elle a elle-même retourné, PLUS le nombre de millions d’années représentées par l’ensemble qu’une autre équipe a retourné.)

PARTIE 3: METTRE DES DATES SUR LES ROCHES ET LES FOSSILES

Pour le schéma fonctionnel (Figure 1) au début de cet exercice, le rapport des atomes U-235:Pb-207 dans la pegmatite est de 1:1 et leur rapport dans le granit est de 1:3. En utilisant le même raisonnement sur les proportions que dans la partie 2b ci-dessus, les élèves peuvent déterminer l’âge de la pegmatite et du granit., Ils devraient écrire les âges de la pegmatite et du granit à côté des noms des roches dans la liste ci-dessous le schéma de principe (Figure 1).

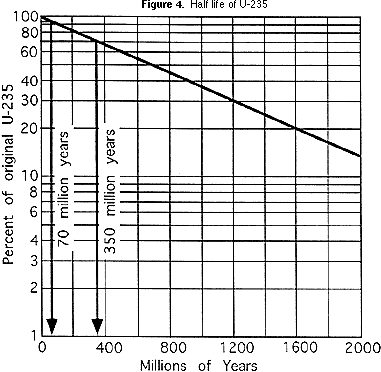
En traçant la demi-vie sur un type d’échelle appelée échelle logarithmique, la ligne courbe comme celle de l’activité M & MTM peut être redressée, comme vous pouvez le voir sur le graphique de la figure 4. Cela rend la courbe plus utile, car il est plus facile de la tracer avec plus de précision. Cela est particulièrement utile pour les rapports d « isotope parent à l » isotope fille qui représentent moins d  » une demi-vie., Pour le schéma fonctionnel (Figure 1), si un laboratoire géochimique détermine que la cendre volcanique qui se trouve dans la siltstone a un rapport U-235:Pb-207 de 47:3 (94% des restes originaux de U-235), cela signifie que la cendre a 70 millions d’années (voir Figure 4). Si le rapport dans le basalte est de 7:3 (70% des restes originaux de U-235), alors le basalte a 350 millions d’années (encore une fois, voir Figure 4). Les élèves doivent écrire l’âge des cendres volcaniques à côté du schiste, de la siltstone et du basalte sur la liste ci-dessous le schéma fonctionnel.,
Retour en haut de page

QUESTIONS À DISCUTER

1) Sur la base des âges radiométriques disponibles, pouvez-vous déterminer l’âge possible de l’unité rocheuse contenant des acritarques et des bactéries? Qu’est-ce que c’est? Pourquoi ne peux-tu pas dire exactement quel est l’âge du rocher?
2) Pouvez-vous déterminer l’âge possible de l’unité rocheuse qui a des trilobites? Qu’est-ce que c’est? Pourquoi ne peux-tu pas dire exactement quel est l’âge du rocher?
3) Quel est l’âge de la roche qui contient les fossiles de Triceratops?, Pourquoi pouvez-vous être plus précis sur l’âge de cette roche que vous ne le pourriez sur l’âge de la roche qui a les trilobites et la roche qui contient des acritarques et des bactéries?

Note pour les enseignants: Sur la base de relations transversales, il a été établi que la pegmatite est plus jeune que l’ardoise et que l’ardoise est plus jeune que le granit. Par conséquent, l’ardoise qui contient l’acritarque et les bactéries a entre 704 millions d’années et 1408 millions d’années, car la pegmatite a 704 millions d’années et le granit a 1408 millions d’années., L  » ardoise elle-même ne peut pas être datée radiométriquement, donc ne peut être entre crochets entre les âges du granit et de la pegmatite.

Le calcaire contenant des trilobites recouvre le grès quartzeux, qui coupe la pegmatite, et le basalte traverse le calcaire. Par conséquent, les trilobites et la roche qui les contient doivent avoir moins de 704 millions d’années (l’âge de la pegmatite) et plus de 350 millions d’années (l’âge du basalte). Le calcaire lui-même ne peut pas être daté radiométriquement, donc ne peut être entre crochets entre les âges du granit et de la pegmatite.,

Les fossiles de dinosaures Triceratops ont environ 70 millions d’années, car ils se trouvent dans le schiste et la siltstone qui contiennent des cendres volcaniques datées radiométriquement à 70 millions d’années. Tous les Tricératops trouvés sous les cendres volcaniques peuvent être un peu plus vieux que 70 millions d’années, et tout trouvé ci-dessus peut être un peu plus jeune que 70 millions d’années., L’âge des Tricératops peut être déterminé plus étroitement que celui des acritarques et des bactéries et que celui des trilobites car l’unité rocheuse qui contient les Tricératops peut elle-même être datée radiométriquement, alors que celle des autres fossiles ne le pourrait pas.