Nous pensons classiquement que la lumière se déplace toujours en lignes droites, mais lorsque les ondes lumineuses passent près d’une barrière, elles ont tendance à se plier autour de cette barrière et à s’étaler. La diffraction de la lumière se produit lorsqu’une onde lumineuse passe par un coin ou à travers une ouverture ou une fente qui est physiquement la taille approximative de, ou même plus petite que la longueur d’onde de cette lumière.,

Une démonstration très simple de la diffraction peut être réalisée en tenant la main devant une source de lumière et en fermant lentement deux doigts tout en observant la lumière transmise entre eux. Au fur et à mesure que les doigts s’approchent et se rapprochent, vous commencez à voir une série de lignes sombres parallèles aux doigts. Les lignes parallèles sont en fait des motifs de diffraction. Ce phénomène peut également se produire lorsque la lumière est « plié » autour des particules qui sont du même ordre de grandeur que la longueur d’onde de la lumière., Un bon exemple de ceci est la diffraction de la lumière du soleil par les nuages que nous appelons souvent une doublure d’argent, illustrée dans la figure 1 avec un magnifique coucher de soleil sur l’océan.
Nous pouvons souvent observer des nuances pastel de bleu, rose, violet et vert dans les nuages qui sont générés lorsque la lumière est diffractée à partir de gouttelettes d’eau dans les nuages. La quantité de diffraction dépend de la longueur d’onde de la lumière, les longueurs d’onde plus courtes étant diffractées à un angle plus grand que les plus longues (en effet, la lumière bleue et violette sont diffractées à un angle plus élevé que la lumière rouge)., Comme une onde lumineuse traversant l’atmosphère rencontre une gouttelette d’eau, comme illustré ci-dessous, elle est d’abord réfractée à l’interface eau:air, puis elle est réfléchie lorsqu’elle rencontre à nouveau l’interface. Le faisceau, voyageant toujours à l’intérieur de la gouttelette d’eau, est à nouveau réfracté lorsqu’il frappe l’interface pour la troisième fois. Cette dernière interaction avec l’interface réfracte la lumière dans l’atmosphère, mais aussi diffracte une partie de la lumière, comme illustré ci-dessous., Cet élément de diffraction conduit à un phénomène connu sous le nom de halo de Cellini (également connu sous le nom d’effet Heiligenschein) où un anneau lumineux de lumière entoure l’ombre de la tête de l’observateur.
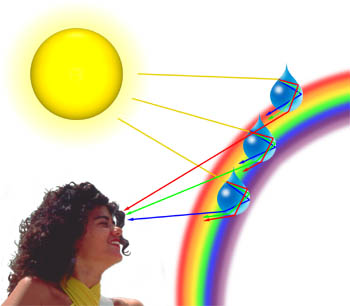
Les termes diffraction et diffusion sont souvent utilisés de manière interchangeable et sont considérés comme presque synonymes. La diffraction décrit un cas spécialisé de diffusion de la lumière dans lequel un objet avec des caractéristiques se répétant régulièrement (telles qu’un réseau de diffraction) produit une diffraction ordonnée de la lumière dans un motif de diffraction., Dans le monde réel, la plupart des objets ont une forme très complexe et doivent être considérés comme composés de nombreuses caractéristiques de diffraction individuelles qui peuvent produire collectivement une diffusion aléatoire de la lumière.
L’un des concepts classiques et les plus fondamentaux impliquant la diffraction est l’expérience de diffraction optique à fente unique, menée pour la première fois au début du XIXe siècle. Lorsqu’une onde lumineuse se propage à travers une fente (ou l’ouverture) le résultat dépend de la taille physique de l’ouverture à l’égard de la longueur d’onde du faisceau incident., Ceci est illustré à la Figure 3 en supposant qu’une onde monochromatique cohérente émise par la source ponctuelle S, semblable à la lumière qui serait produite par un laser, traverse l’ouverture d et est diffractée, le faisceau lumineux incident primaire atterrissant au point P et les premiers maxima secondaires se produisant au point Q.
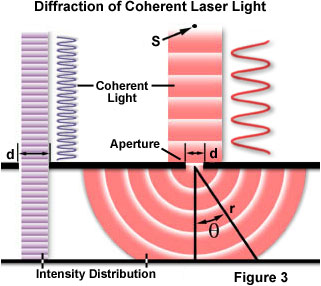
Comme indiqué sur le côté gauche de la figure, lorsque la longueur d’onde (λ) est beaucoup plus petite que la largeur de l’ouverture (d), l’onde se déplace simplement en ligne droite, tout comme il le ferait si elle était une particule ou aucune ouverture étaient présents., Cependant, lorsque la longueur d’onde dépasse la taille de l’ouverture, on subit une diffraction de la lumière selon l’équation:
Où θ est l’angle entre la direction de propagation centrale incidente et le premier minimum du motif de diffraction. L’expérience produit un maximum central lumineux qui est flanqué des deux côtés par des maxima secondaires, l’intensité de chaque maximum secondaire suivant diminuant à mesure que la distance du centre augmente. La figure 4 illustre ce point avec un tracé de l’intensité du faisceau par rapport au rayon de diffraction., Notez que les minima se produisant entre les maxima secondaires sont situés en multiples de π.
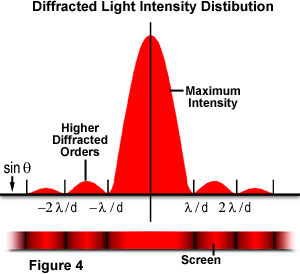
Cette expérience a d’abord été expliquée par Augustin Fresnel qui, avec Thomas Young, a produit des preuves importantes confirmant que la lumière se déplace par vagues. À partir des figures ci-dessus, nous voyons comment une lumière monochromatique cohérente (dans cet exemple, un éclairage laser) émise par le point L est diffractée par l’ouverture d., Fresnel suppose que l’amplitude de la première commande maxima au point Q (défini comme eQ) serait donnée par l’équation:
où A est l’amplitude de l’onde incidente, r est la distance entre d et Q, et f(χ) est une fonction de x, l’inclination facteur introduit par Fresnel.
Diffraction de la lumière
Explorez comment un faisceau de lumière est diffracté lorsqu’il traverse une fente ou une ouverture étroite. Ajustez la longueur d’onde et la taille de l’ouverture et observez comment cela affecte le modèle d’intensité de diffraction.,
La diffraction de la lumière joue un rôle primordial dans la limitation du pouvoir de résolution de tout instrument optique (par exemple: caméras, jumelles, télescopes, microscopes et l’œil). Le pouvoir de résolution est la capacité de l’instrument optique à produire des images séparées de deux points adjacents. C’est souvent déterminée par la qualité des lentilles et de miroirs dans l’instrument ainsi que les propriétés du milieu environnant (généralement de l’air). La nature ondulatoire de la lumière force une limite ultime au pouvoir de résolution de tous les instruments optiques.,
Nos discussions sur la diffraction ont utilisé une fente comme ouverture à travers laquelle la lumière est diffractée. Cependant, tous les instruments optiques ont des ouvertures circulaires, par exemple la pupille d’un œil ou le diaphragme circulaire et les lentilles d’un microscope. Les ouvertures circulaires produisent des motifs de diffraction similaires à ceux décrits ci-dessus, sauf que le motif présente naturellement une symétrie circulaire. L’analyse mathématique des motifs de diffraction produits par une ouverture circulaire est décrite par l’équation:
où θ(1) est la position angulaire du premier ordre de diffraction des minima (le premier anneau noir), λ est la longueur d’onde de la lumière incidente, d est le diamètre de l’ouverture, et 1,22 est une constante. Dans la plupart des cas, l’angle θ(1) étant très petit, l’approximation selon laquelle le sin et le tan de l’angle sont presque égaux donne:
À partir de ces équations, il devient évident que le maximum central est directement proportionnel à λ/d, ce qui rend ce maximum plus étalé pour les longueurs d’onde plus longues et pour les ouvertures plus petites., La mimina secondaire de diffraction a fixé une limite au grossissement utile des lentilles d’objectif en microscopie optique, en raison de la diffraction inhérente de la lumière par ces lentilles. Quelle que soit la perfection de l’objectif, l’image d’une source ponctuelle de lumière produite par l’objectif est accompagnée de maxima d’ordre secondaire et supérieur. Cela ne pourrait être éliminé que si la lentille avait un diamètre infini. Deux objets séparés par une distance inférieure à θ(1) ne peuvent pas être résolus, quelle que soit la puissance de grossissement., Bien que ces équations aient été dérivées pour l’image d’une source ponctuelle de lumière à une distance infinie de l’ouverture, il s’agit d’une approximation raisonnable du pouvoir de résolution d’un microscope lorsque d est substitué au diamètre de l’objectif.
Ainsi, si deux objets résident à une distance D l’un de l’autre et sont à une distance L d’un observateur, l’angle (exprimé en radians) entre eux est:
ce qui nous amène à pouvoir condenser les deux dernières équations pour donner:
Où D (0) est la distance minimale de séparation entre les objets qui permettra de les résoudre. En utilisant cette équation, l’œil humain peut résoudre des objets séparés par une distance de 0,056 millimètre, mais les photorécepteurs de la rétine ne sont pas assez proches les uns des autres pour permettre ce degré de résolution, et 0,1 millimètre est un nombre plus réaliste dans des circonstances normales.
Le pouvoir de résolution des microscopes optiques est déterminé par un certain nombre de facteurs, y compris ceux discutés, mais dans les circonstances les plus idéales, ce nombre est d’environ 0,2 micromètre., Ce nombre doit tenir compte de l’alignement optique du microscope, de la qualité des lentilles, ainsi que des longueurs d’onde prédominantes de la lumière utilisées pour l’image de l’échantillon. Bien qu’il ne soit souvent pas nécessaire de calculer le pouvoir de résolution exact de chaque objectif (et serait une perte de temps dans la plupart des cas), il est important de comprendre les capacités des lentilles de microscope telles qu’elles s’appliquent au monde réel.
Auteurs contributeurs
Mortimer Abramowitz – Olympus America, Inc., Deux Centre d’Entreprise Drive., Melville, New York, 11747.
Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Université d’État de Floride, Tallahassee, Floride, 32310.