L’un des plus grands aspects de Sudoku est que le jeu offre des défis engageants à la fois le novice, ainsi que le joueur de puzzle chevronné. Chaque fois qu’ils jouent un puzzle adapté à leur niveau de compétence, le débutant et le solveur de Sudoku expérimenté devront mettre une bonne quantité de réflexion et de technique dans l’accomplissement de la tâche. Leur approche, cependant, peut ne pas être la même. Résoudre un puzzle de Sudoku dur nécessitera un ensemble de techniques tout à fait différent par rapport à un facile., Cet article présente neuf de ces techniques; en difficulté croissante.
Lors de l’utilisation de ces techniques, la façon dont les pros préfèrent le faire, c’est de commencer par la base. Utilisez les premières techniques pour insérer autant de chiffres que possible. Ensuite, lorsque vous ne pouvez plus ajouter de chiffres au tableau en utilisant les techniques de base, essayez les plus avancées. Faites un à la fois jusqu’à ce que vous puissiez tracer un nombre de plus dans une cellule. Ensuite, recommencez avec les techniques de base et répétez le processus. Vous devriez être capable de résoudre presque n’importe quel puzzle de Sudoku en utilisant ces techniques.,
Techniques de suppression des nombres:
Candidat unique
Lorsqu’une cellule spécifique ne peut contenir qu’un seul nombre, ce nombre est un « candidat unique ». Cela se produit chaque fois que tous les autres numéros, sauf le numéro candidat, existent dans le bloc, la colonne ou la ligne en cours. Dans cet exemple, la cellule rouge ne peut contenir que le nombre 5, car les huit autres nombres ont tous été utilisés dans le bloc, la colonne et la ligne associés.,
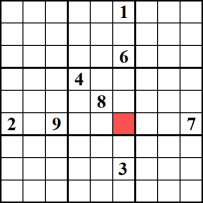
Candidat unique
Vous savez que chaque bloc, ligne et colonne d’une carte de Sudoku doit contenir tous les nombres compris entre 1 et 9. Par conséquent, si un nombre, disons 4, ne peut être placé que dans une seule cellule dans un bloc/colonne/ligne, alors ce nombre est garanti pour y tenir. Cet exemple illustre le nombre 4 comme candidat unique pour la cellule marquée en rouge.,
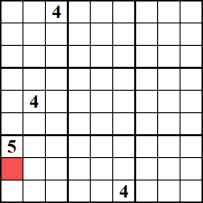
Techniques pour supprimer les candidats:
Interaction bloc et colonne / ligne
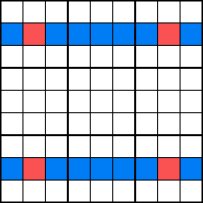
Cette méthode ne vous aidera pas à tracer de nouveaux nombres, mais elle vous aidera à dans une ligne ou une colonne spécifique. L’exemple montre que le nombre 7 ne peut être inséré que dans les cellules rouges de la rangée du milieu. Ainsi, vous pouvez supprimer 7 comme candidat possible du reste de la ligne.,
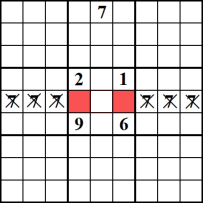
Bloc / Bloc Interaction
Cette technique est mieux compris en regardant l’exemple. Dans les blocs du milieu et du milieu gauche, le numéro 8 doit être placé dans l’un des globules rouges. Cela signifie que nous pouvons éliminer 8 des rangées supérieure et inférieure de la colonne du milieu à droite.,
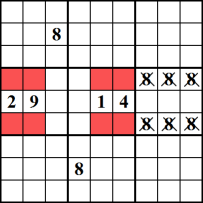
Sous-ensemble nu
L’exemple montre que la ligne numéro 1 et la ligne numéro 5 ont toutes deux une cellule dans la même colonne contenant uniquement les numéros candidats 4 et 7. Ces deux nombres apparaissent également en tant que candidats dans toutes les autres cellules ouvertes de cette colonne, mais comme ils sont les deux seuls candidats des lignes 1 et 5, ces deux nombres ne peuvent pas apparaître ailleurs dans la ligne, vous pouvez donc les supprimer. Dans l’exemple, les deux candidats paires encerclé en rouge, sont les seuls candidats., Étant donné que 4 et 7 doivent être placés dans l’une ou l’autre de ces deux cellules, toutes les paires entourées en bleu peuvent supprimer ces numéros en tant que candidats. Dans ce puzzle, cela signifie que 1 devient seul candidat dans la deuxième rangée; 2 devient seul candidat dans la rangée 6; et ainsi, 6 est seul candidat pour la rangée numéro 4.
Vous pouvez également utiliser cette technique si vous avez plus de deux candidats. Par exemple, disons que les paires encerclées en rouge étaient plutôt des candidats triples des nombres 1, 4, 7. Cela signifierait que ces trois numéros devraient être placés dans les lignes 1, 2 ou 5., Nous pourrions supprimer ces trois numéros en tant que candidats dans l’une des cellules restantes de la colonne. Cette technique fonctionne même avec quatre numéros de candidat, en supposant que vous avez 4 candidats possibles dans quatre cellules différentes dans une ligne / colonne.
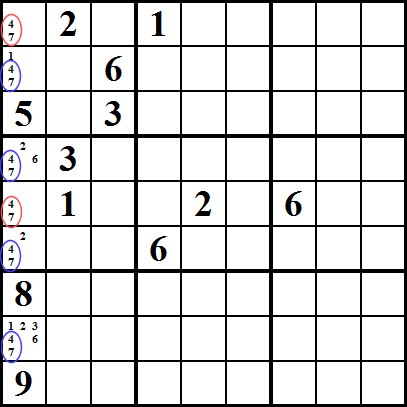
Masqué sous-ensemble
Ceci est similaire à Nu, sous-ensemble, mais il affecte les cellules de la tenue de la les candidats., Dans cet exemple, nous voyons que les nombres 5, 6, 7 ne peuvent être placés que dans les cellules 5 ou 6 de la première colonne (marquées dans un cercle rouge), et que le nombre 5 ne peut être inséré que dans la cellule numéro 8 (marquées dans un cercle bleu). Puisque 6 et 7 doivent être placés dans l’une des cellules avec un cercle rouge, il s’ensuit que le nombre 5 doit être placé dans la cellule numéro 8, et ainsi nous pouvons retirer tous les autres candidats de la 8ème cellule; dans ce cas, 2 et 3.,
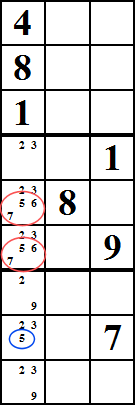
X-Wing
Cette méthode permet de travailler quand vous regardez cellules comprenant un rectangle, tel que les cellules marquées en rouge. Dans cet exemple, disons que les cellules rouges et bleues ont toutes le numéro 5 comme numéros candidats. Maintenant, imaginez si les globules rouges sont les seules cellules de la colonne 2 et 8 dans lesquelles vous pouvez mettre 5.
Dans ce cas, vous devez évidemment mettre un 5 dans deux des globules rouges, et vous savez également qu’ils ne peuvent pas tous les deux être dans la même rangée., Eh bien, maintenant, cela signifie que vous pouvez éliminer 5 comme candidat pour toutes les cellules bleues. En effet, dans la rangée supérieure, la première ou la deuxième cellule rouge doit avoir un 5, et la même chose peut être dite à propos de la rangée inférieure.
l’Espadon
l’Espadon est un plus compliqué que la version de X-Wing. Dans la plupart des cas, la technique peut sembler beaucoup de travail pour très peu de salaire, mais certains puzzles ne peuvent être résolus qu’avec elle. Donc, si vous voulez être un maître de la résolution de sudoku, lisez la suite!,
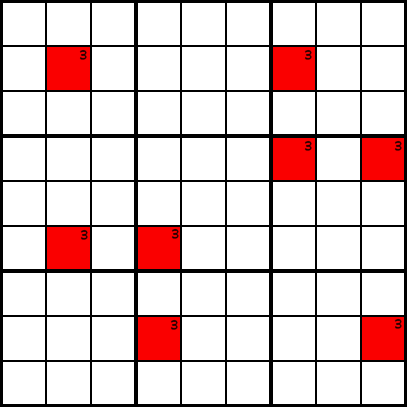ExempleDans l’exemple A, nous avons tracé dans certaines cellules candidates pour le numéro 3. Maintenant, supposons que dans les colonnes 2, 4, 7 et 9, les seules cellules pouvant contenir le chiffre 3 sont celles marquées en rouge. Vous savez que chaque colonne doit contenir un 3.
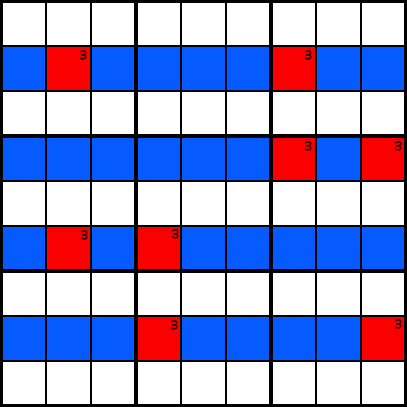Exemple BRegardez l’exemple B. Nous pouvons éliminer les 3 candidats dans toutes les cellules marquées en bleu., La raison en est que si nous considérons les placements possibles du nombre 3 dans les cellules rouges, nous obtenons deux alternatives: soit vous devez mettre 3s dans les cellules vertes, soit dans les cellules violettes, comme le montre l’exemple C. Dans tous les cas, chacune des colonnes 2, 4, 7 et 9, doit contenir un 3 dans l’une des cellules colorées, de sorte qu’aucune autre cellule de ces lignes ne peut contenir un 3.
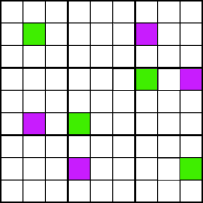Exemple CComment reconnaître un espadon modèle? Vous recherchez des cellules avec des numéros candidats communs qui peuvent être enchaînés ensemble comme dans l’exemple D., Si vous commencez, disons, la cellule rouge en haut à gauche. Ensuite, vous tracez une ligne verticalement ou horizontalement jusqu’à ce que vous atteigniez une autre cellule contenant le même numéro de candidat. Ensuite, vous répétez ce modèle jusqu’à ce que vous reveniez à la cellule d’origine. Si vous atteignez la cellule d’origine, vous avez un espadon modèle!
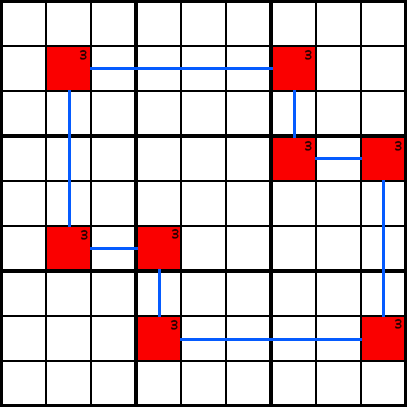Exemple DChaîne de forçage
Chaîne de forçage peut réellement vous aider à déterminer exactement quel nombre une certaine cellule doit contenir. Malheureusement, la technique n’est pas la plus facile à utiliser., Regardez l’exemple ci-dessous. Supposons que les candidats dans les globules rouges sont les seuls candidats pour ces cellules.
Les chaînes de forçage fonctionnent de la manière suivante: Commencez sur la cellule rouge avec la flèche pointant vers elle, et remplissez l’un des deux candidats, 3 ou 6, pour cette cellule. Ensuite, suivez et remplissez le reste des globules rouges. Maintenant, prenez note des valeurs que vous entrez en cours de route. Revenez à la cellule avec laquelle vous avez commencé et essayez l’autre numéro candidat pour cette cellule, et remplissez également les autres globules rouges. Comparez les chiffres que vous avez maintenant avec le premier résultat., Vous pouvez constater que dans les deux cas, une certaine cellule doit contenir un numéro spécifique.
Dans cet exemple, si vous mettez le nombre 3 dans la cellule de départ, vous verrez que la cellule voisine ci-dessus à droite doit contenir un 9. Maintenant, essayez d’entrer un 6 dans la cellule de départ à la place, et déplacez-vous dans l’autre sens, en entrant des valeurs candidates. Lorsque vous atteignez à nouveau la cellule voisine ci-dessus à droite, vous constaterez qu’elle doit contenir un 9 cette fois-ci aussi. Ainsi cette cellule doit contenir un 9.
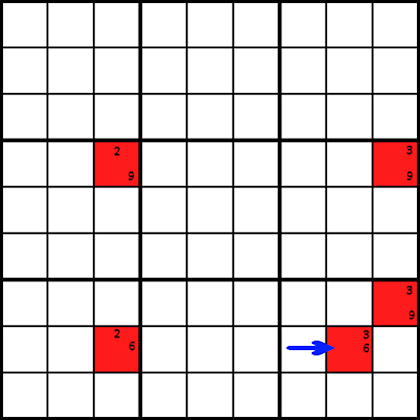
c’est tout., J’espère que cela vous aidera à casser même les puzzles de sudoku les plus difficiles là-bas. Bonne chance!
Cet article fait partie de notre section d’aide Sudoku.
Play Sudoku Epic
Sudoku Epic est un jeu de Sudoku gratuit de qualité supérieure et est disponible sur la plupart des plates-formes: PC, Mac, iPhone, iPad, Android, Google Play Store et Amazon Appstore.
Sudoku Épique sur Google Play
Sudoku Épique sur iPhone/iPad