les Résultats de l’Apprentissage
- Identifier les foyers, des sommets, des haches, et le centre d’une ellipse.
- Écrire des équations d’ellipses centrées à l’origine.
- Écrire des équations d’ellipses non centrées à l’origine.
Une conique ou conique, est une forme résultant de l’intersection d’une droite circulaire du cône avec un plan. L’angle auquel le plan coupe le cône détermine la forme.,
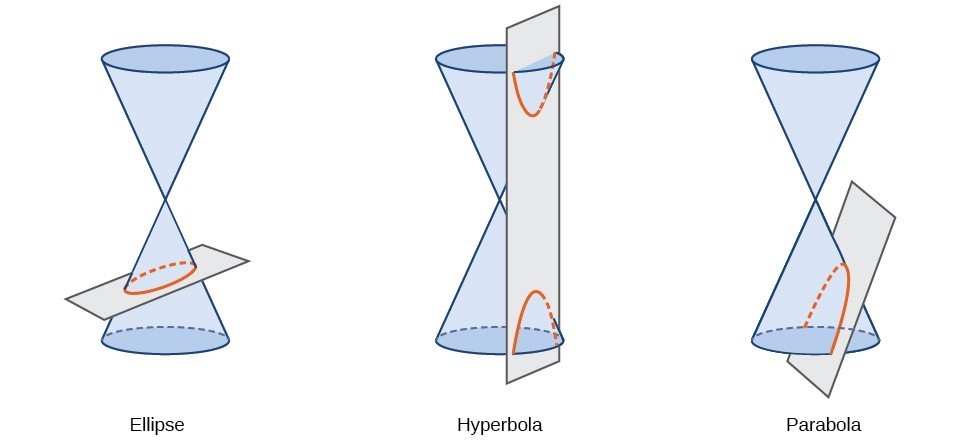
Les sections coniques peuvent également être décrites par un ensemble de points dans le plan de coordonnées. Plus loin dans ce chapitre, nous verrons que le graphique de toute équation quadratique en deux variables est une section conique. Les signes des équations et les coefficients des termes variables déterminent la forme. Cette section se concentre sur les quatre variations de la forme standard de l’équation de l’ellipse. Une ellipse est l’ensemble de tous les points \left (x, y\right) dans un plan tel que la somme de leurs distances à partir de deux points fixes est une constante., Chaque point fixe est appelé foyer (pluriel: foyers) de l’ellipse.
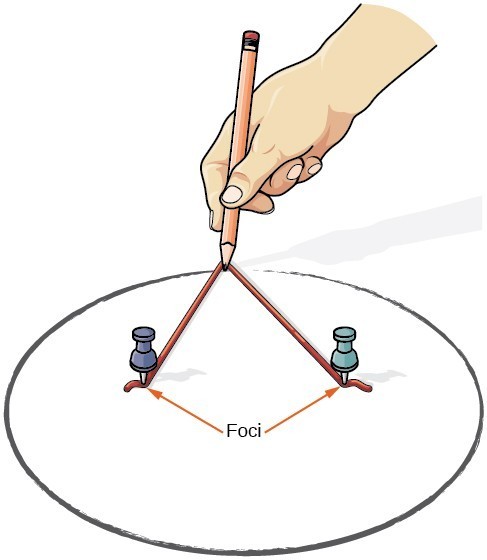
Nous pouvons dessiner une ellipse à l’aide d’un morceau de carton, de deux punaises, d’un crayon et d’une ficelle. Placer les punaises dans le carton pour former les foyers de l’ellipse. Coupez un morceau de chaîne plus long que la distance entre les deux punaises (la longueur de la chaîne représente la constante dans la définition). Collez chaque extrémité de la ficelle sur le carton et tracez une courbe avec un crayon tendu contre la ficelle. Le résultat est une ellipse.
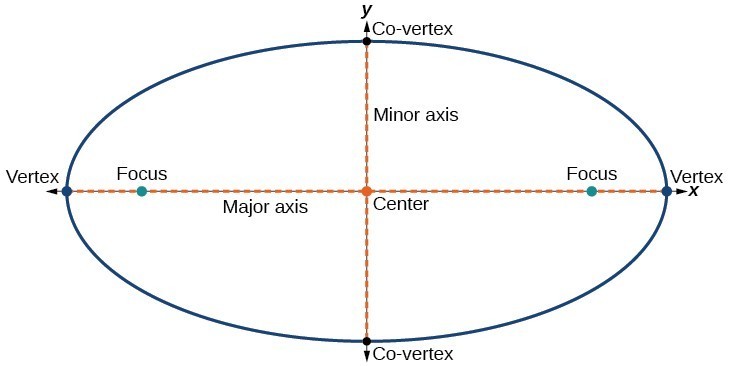
Chaque ellipse a deux axes de symétrie., L’axe le plus long est appelé l’axe majeur et l’axe le plus court est appelé l’axe mineur. Chaque extrémité de l’axe majeur est le sommet de l’ellipse (pluriel: des sommets), et à chaque extrémité de l’axe mineur est une co-sommet de l’ellipse. Le centre d’une ellipse est le point médian des axes majeur et mineur. Les axes sont perpendiculaires au centre. Les foyers se trouvent toujours sur le grand axe, et la somme des distances entre les foyers et n’importe quel point de l’ellipse (la somme constante) est supérieure à la distance entre les foyers.,
Dans cette section, nous limitons l’ellipse à ceux qui sont positionnés verticalement ou horizontalement dans le coordonner avion. Autrement dit, les axes seront soit situés sur ou parallèles aux axes x et y. Plus tard dans le chapitre, nous verrons des ellipses qui sont tournées dans le plan de coordonnées.
Pour travailler avec des ellipses horizontales et verticales dans le plan de coordonnées, nous considérons deux cas: ceux qui sont centrés à l’origine et ceux qui sont centrés en un point autre que l’origine., Nous apprendrons d’abord à dériver les équations d’ellipses, puis nous apprendrons à écrire les équations d’ellipses sous forme standard. Plus tard, nous utiliserons ce que nous apprenons pour dessiner les graphiques.,v>Si (x,y) est un point de l’ellipse, alors on peut définir les variables suivantes:
\begin{align}d_1&=\text{la distance de } (-c,0) \text{ pour } (x,y) \\ d_2&= \text{la distance de } (c,0) \text{ pour } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
pour une ellipse centrée à l’origine avec son grand axe sur l’axe des X et
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
pour une ellipse centrée à l’origine avec son grand axe sur l’axe des ordonnées.,
Écriture d’équations d’Ellipses Non centrées à l’origine
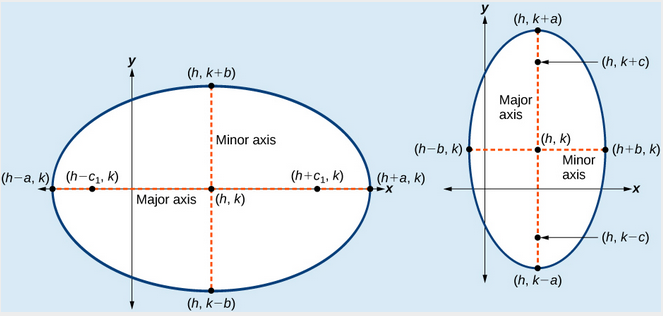
(a) Ellipse horizontale avec centre \gauche(h,k\droite) (b) Ellipse verticale avec centre \gauche(h,k\droite)
Résolution de Problèmes appliqués impliquant des Ellipses
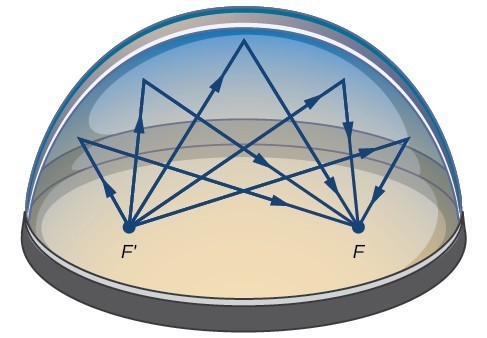
De nombreuses situations réelles peuvent être représentées par des ellipses, y compris des orbites de planètes, de satellites, de lunes et de comètes, et des formes de quilles de bateaux, de gouvernails et d’ailes d’avions. Un dispositif médical appelé lithotripteur utilise des réflecteurs elliptiques pour briser les calculs rénaux en générant des ondes sonores., Certains bâtiments, appelés whispering chambers, sont conçus avec des dômes elliptiques de sorte qu’une personne chuchotant à un foyer peut facilement être entendue par quelqu’un debout à l’autre foyer. Cela se produit en raison des propriétés acoustiques d’une ellipse. Lorsqu’une onde sonore provient d’un foyer d’une chambre de chuchotement, l’onde sonore est réfléchie par le dôme elliptique et retourne à l’autre foyer. Dans la chambre whisper du Musée des Sciences et de l’Industrie de Chicago, deux personnes debout près des foyers—à environ 43 pieds l’un de l’autre—peuvent s’entendre chuchoter.