Résistances par rapport aux inducteurs
Les inducteurs ne se comportent pas de la même manière que les résistances. Alors que les résistances s’opposent simplement au flux de courant à travers elles (en laissant tomber une tension directement proportionnelle au courant), les inductances s’opposent aux changements de courant à travers elles, en laissant tomber une tension directement proportionnelle au taux de changement de courant.
Conformément à la loi de Lenz, cette tension induite est toujours d’une polarité telle qu’elle essaie de maintenir le courant à sa valeur actuelle., C’est-à-dire que si le courant augmente en amplitude, la tension induite « poussera contre” le flux de courant; si le courant diminue, la polarité s’inversera et « poussera avec” le courant pour s’opposer à la diminution.
Cette opposition au changement de courant est appelée réactance, plutôt que résistance., Exprimée mathématiquement, la relation entre la tension tombée à travers l’inducteur et le taux de changement de courant à travers l’inducteur est en tant que telle:

Courant alternatif dans un Circuit inductif simple
L’expression di/dt est une de calcul, c’est-à-dire la vitesse de changement du courant instantané (i) au fil du temps, en ampères par seconde.
L’inductance (L) est en Henrys, et la tension instantanée (e), bien sûr, est en volts., Parfois, vous trouverez le taux de tension instantanée exprimé en « v” au lieu de « e” (v = L di/dt), mais cela signifie exactement la même chose.
Pour montrer ce qui se passe avec le courant alternatif, analysons un circuit inducteur simple:
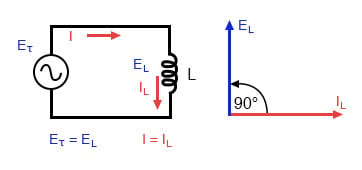
Circuit inductif pur: Le courant de l’inducteur accuse un retard de 90°sur la tension de l’inducteur.
Si nous devions tracer le courant et la tension pour ce circuit très simple, cela ressemblerait à ceci:

Circuit inductif pur, formes d’onde.,
Rappelez-vous que la chute de tension à travers une inductance est une réaction contre le changement de courant à travers elle.
Par conséquent, la tension instantanée est nulle chaque fois que le courant instantané est à un pic (changement de zéro, ou pente de niveau, sur l’onde sinusoïdale actuelle), et la tension instantanée est à un pic partout où le courant instantané est à un changement maximal (les points de pente la plus raide sur l’onde actuelle, où
Il en résulte une onde de tension déphasée de 90° par rapport à l’onde de courant., En regardant le graphique, l’onde de tension semble avoir une” longueur d’avance « sur l’onde de courant; la tension” conduit « le courant et le courant” traîne » derrière la tension.

Courant gal de tension par pas de 90° dans un pur circuit inductif.
les Choses deviennent encore plus intéressantes si on fait un graphique de la puissance de ce circuit:

Dans un pur circuit à induction, puissance instantanée peut être positif ou négatif.,
Étant donné que la puissance instantanée est le produit de la tension instantanée et du courant instantané (p=ie), la puissance est égale à zéro chaque fois que le courant ou la tension instantanée est égal à zéro. Chaque fois que le courant instantané et la tension sont tous deux positifs (au-dessus de la ligne), la puissance est positive.
Comme pour l’exemple de résistance, la puissance est également positive lorsque le courant instantané et la tension sont tous deux négatifs (en dessous de la ligne).,
Cependant, parce que les ondes de courant et de tension sont déphasées à 90°, il y a des moments où l’une est positive tandis que l’autre est négative, ce qui entraîne des occurrences tout aussi fréquentes de puissance instantanée négative.
Qu’est-ce que le pouvoir négatif?
Mais que signifie le pouvoir négatif? Cela signifie que l’inducteur libère de la puissance dans le circuit, tandis qu’une puissance positive signifie qu’il absorbe la puissance du circuit.,
Étant donné que les cycles de puissance positive et négative sont égaux en amplitude et en durée au fil du temps, l’inducteur libère autant de puissance dans le circuit qu’il en absorbe sur la durée d’un cycle complet.
Cela signifie concrètement que la réactance d’un inducteur dissipe une énergie nette de zéro, tout à fait contrairement à la résistance d’une résistance, qui dissipe l’énergie sous forme de chaleur. Rappelez-vous, c’est pour les inducteurs parfaits seulement, qui n’ont aucune résistance de fil.
Réactance vs, Résistance
L’opposition d’une inductance au changement de courant se traduit par une opposition au courant alternatif en général, qui change par définition toujours en amplitude et en direction instantanées.
Cette opposition au courant alternatif est similaire à la résistance mais différente en ce qu’elle entraîne toujours un déphasage entre le courant et la tension, et qu’elle dissipe une puissance nulle. En raison des différences, il a un nom différent: réactance. La réactance à AC est exprimée en ohms, tout comme la résistance est, sauf que son symbole mathématique est X au lieu de R.,
Pour être précis, la réactance associée à une inductance est généralement symbolisée par la lettre majuscule X avec une lettre L comme indice, comme ceci: XL.
Étant donné que les inducteurs chutent la tension proportionnellement au taux de changement de courant, ils chuteront plus de tension pour les courants à changement plus rapide, et moins de tension pour les courants Cela signifie que la réactance en ohms pour tout inducteur est directement proportionnelle à la fréquence du courant alternatif., La formule exacte pour déterminer la réactance est la suivante:

Si nous exposons un inducteur de 10 mH à des fréquences de 60, 120 et 2500 Hz, il manifestera les réactances dans le tableau ci-dessous.
la Réactance de 10 mH inducteur:
| Fréquence (Hertz) | Réactance (Ohms) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
Dans l’équation de réactance, le terme « 2nf” (tout sur le côté droit sauf le L) a une signification particulière en soi. C’est le nombre de radians par seconde auquel le courant alternatif « tourne”, si vous imaginez un cycle de courant alternatif pour représenter la rotation d’un cercle complet.
Un radian est une unité de mesure d’angle: il y a 2π radians dans un cercle complet, tout comme il y a 360° dans un cercle complet., Si l’alternateur produisant le C. A. est une unité bipolaire, il produira un cycle pour chaque tour complet de rotation d’axe, qui est tous les 2π radians, ou 360°.
Si cette constante de 2π est multipliée par la fréquence en Hertz (cycles par seconde), le résultat sera un chiffre en radians par seconde, connu sous le nom de vitesse angulaire du système AC.
Vitesse angulaire dans les systèmes AC
La vitesse angulaire peut être représentée par l’expression 2nf, ou elle peut être représentée par son propre symbole, la lettre grecque minuscule omega, qui apparaît similaire à notre minuscule romain « w”: ω., Ainsi, la formule de réactance XL = 2nfL pourrait également s’écrire XL = wL.
Il faut comprendre que cette « vitesse angulaire” est une expression de la vitesse à laquelle les formes d’onde AC font un cycle, un cycle complet étant égal à 2π radians. Il n’est pas nécessairement représentatif de la vitesse réelle de l’arbre de l’alternateur produisant le courant alternatif.
Si l’alternateur a plus de deux pôles, la vitesse angulaire sera un multiple de la vitesse de l’arbre., Pour cette raison, ω est parfois exprimé en unités de radians électriques par seconde plutôt qu’en radians (simples) par seconde, de manière à le distinguer du mouvement mécanique.
de Toute manière d’exprimer la vitesse angulaire du système, il est évident que c’est directement proportionnelle à la réactance dans l’inducteur. Lorsque la fréquence (ou la vitesse de l’arbre de l’alternateur) augmente dans un système alternatif, un inducteur offre une plus grande opposition au passage du courant, et vice versa.,
Le courant alternatif dans un circuit inductif simple est égal à la tension (en volts) divisée par la réactance inductive (en ohms), tout comme le courant alternatif ou continu dans un circuit résistif simple est égal à la tension (en volts) divisée par la résistance (en ohms). Un exemple de circuit est illustré ici:

réactance Inductive

des Angles de Phase
Cependant, nous devons garder à l’esprit que la tension et le courant ne sont pas en phase., Comme indiqué précédemment, la tension a un déphasage de +90° par rapport au courant. Si nous représentons mathématiquement ces angles de phase de tension et de courant sous la forme de nombres complexes, nous constatons que l’opposition d’une inductance au courant a également un angle de phase:


de 90° dans une inductance.
Mathématiquement, nous disons que l’angle de phase de l’opposition d’une inductance au courant est de 90°, ce qui signifie que l’opposition d’une inductance au courant est une quantité imaginaire positive., Cet angle de phase d’opposition réactive au courant devient d’une importance critique dans l’analyse de circuits, en particulier pour les circuits AC complexes où la réactance et la résistance interagissent.
Il s’avérera avantageux de représenter l’opposition de n’importe quel composant au courant en termes de nombres complexes plutôt que de quantités scalaires de résistance et de réactance.
REVIEW:
- La réactance inductive est l’opposition qu’une inductance offre au courant alternatif en raison de son stockage déphasé et de sa libération d’énergie dans son champ magnétique., La réactance est symbolisée par la lettre majuscule « X” et est mesurée en ohms tout comme la résistance (R).
- La réactance inductive peut être calculée en utilisant cette formule: XL = 2nfL
- La vitesse angulaire d’un circuit alternatif est une autre façon d’exprimer sa fréquence, en unités de radians électriques par seconde au lieu de cycles par seconde. Il est symbolisé par la lettre grecque minuscule « omega”, ou ω.
- La réactance inductive augmente avec la fréquence croissante. En d’autres termes, plus la fréquence est élevée, plus elle s’oppose au flux alternatif d’électrons.,
FEUILLES DE CALCUL CONNEXES:
- Feuille de calcul des inducteurs
- Feuille de calcul de la réactance inductive