Introduction
La régression linéaire, également connue sous le nom de régression linéaire simple ou de régression linéaire bivariée, est utilisée lorsque nous voulons prédire la valeur Par exemple, vous pouvez utiliser la régression linéaire pour comprendre si les performances de l’examen peuvent être prédites en fonction du temps de révision (c’est-à-dire,, votre variable dépendante serait « performance de l’examen », mesurée de 0 à 100 points, et votre variable indépendante serait » temps de révision », mesuré en heures). Alternativement, vous pouvez utiliser la régression linéaire pour comprendre si la consommation de cigarettes peut être prédite en fonction de la durée du tabagisme (c.-à-d., votre variable dépendante serait la « consommation de cigarettes », mesurée en termes de nombre de cigarettes consommées quotidiennement, et votre variable indépendante serait la « durée du tabagisme », mesurée en jours). Si vous avez deux ou plusieurs variables indépendantes, plutôt qu’une seule, vous devez utiliser la régression multiple., Alternativement, si vous souhaitez simplement établir si une relation linéaire existe, vous pouvez utiliser la corrélation de Pearson.
Remarque: La variable dépendante est également appelée variable de résultat, cible ou critère, tandis que la variable indépendante est également appelée variable prédictive, explicative ou régresseuse. En fin de compte, quel que soit le terme que vous utilisez, il est préférable d’être cohérent. Nous les appellerons variables dépendantes et indépendantes tout au long de ce guide.,
Dans ce guide, nous vous montrons comment réaliser une régression linéaire à l’aide de Stata, ainsi que d’interpréter et présenter les résultats de ce test. Cependant, avant de vous présenter cette procédure, vous devez comprendre les différentes hypothèses que vos données doivent respecter pour que la régression linéaire vous donne un résultat valide. Nous discutons ensuite de ces hypothèses.
Stata
Hypothèses
Il existe sept « hypothèses » qui sous-tendent la régression linéaire. Si l’une de ces sept hypothèses n’est pas remplie, vous ne pouvez pas analyser vos données en utilisant linear car vous n’obtiendrez pas de résultat valide., Étant donné que les hypothèses nos 1 et 2 se rapportent à votre choix de variables, elles ne peuvent pas être testées pour utiliser Stata. Cependant, vous devez décider si votre étude répond à ces hypothèses avant de passer.
- Hypothèse #1: Votre variable dépendante doit être mesurée au niveau continue., Des exemples de telles variables continues incluent la taille (mesurée en pieds et en pouces), la température (mesurée en oC), le salaire (mesuré en dollars américains), le temps de révision (mesuré en heures), l’intelligence (mesurée à l’aide du score de QI), le temps de réaction (mesuré en millisecondes), la performance des tests (mesurée de 0 à 100), les Si vous ne savez pas si votre variable dépendante est continue (c.-à-d. mesurée au niveau de l’intervalle ou du rapport), consultez notre guide des types de variables.,
- Hypothèse # 2: Votre variable indépendante doit être mesurée au niveau continu ou catégorique. Cependant, si vous avez une variable indépendante catégorielle, il est plus courant d’utiliser un test t indépendant (pour 2 groupes) ou une ANOVA unidirectionnelle (pour 3 groupes ou plus). En cas de doute, des exemples de variables catégorielles incluent le sexe (p. ex., 2 groupes: hommes et femmes), l’ethnicité( p. ex., 3 groupes: Caucasiens, Afro-Américains et hispaniques), le niveau d’activité physique (p. ex., 4 groupes: sédentaires, faibles, modérés et élevés) et la profession (p. ex.,, 5 groupes: chirurgien, médecin, infirmier, dentiste, ergothérapeute). Dans ce guide, nous vous montrons la procédure de régression linéaire et la sortie Stata lorsque vos variables dépendantes et indépendantes ont été mesurées à un niveau continu.
Heureusement, vous pouvez vérifier les hypothèses #3, #4, #5, #6 et #7 en utilisant Stata. En passant aux hypothèses #3, #4, #5, #6 et # 7, nous suggérons de les tester dans cet ordre car il représente un ordre où, si une violation de l’hypothèse n’est pas corrigible, vous ne pourrez plus utiliser la régression linéaire., En fait, ne soyez pas surpris si vos données échouent à une ou plusieurs de ces hypothèses, car cela est assez typique lorsque vous travaillez avec des données réelles plutôt que des exemples manuels, qui ne vous montrent souvent comment effectuer une régression linéaire que lorsque tout se passe bien. Cependant, ne vous inquiétez pas car même lorsque vos données échouent à certaines hypothèses, il existe souvent une solution pour surmonter cela (par exemple, transformer vos données ou utiliser un autre test statistique à la place)., Rappelez-vous simplement que si vous ne vérifiez pas que vos données répondent à ces hypothèses ou si vous les testez incorrectement, les résultats que vous obtenez lors de l’exécution de la régression linéaire peuvent ne pas être valides.
- Hypothèse #3: Il doit y avoir une relation linéaire entre les variables dépendantes et indépendantes. Bien qu’il existe un certain nombre de façons de vérifier si une relation linéaire existe entre vos deux variables, nous vous suggérons de créer un nuage de points à l’aide de Stata, où vous pouvez tracer la variable dépendante par rapport à votre variable indépendante., Vous pouvez ensuite inspecter visuellement le nuage de points pour vérifier la linéarité. Votre nuage de points peut ressembler à l’un des éléments suivants:
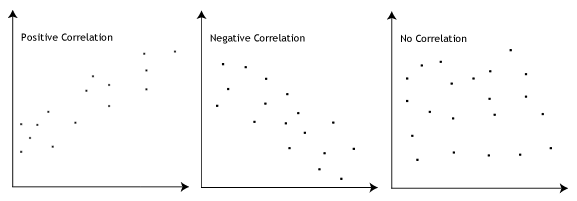
Si la relation affichée dans votre nuage de points n’est pas linéaire, vous devrez exécuter une analyse de régression non linéaire ou « transformer » vos données, ce que vous pouvez faire en utilisant Stata.
- Hypothèse no 4: Il ne devrait pas y avoir de valeurs aberrantes significatives. Les valeurs aberrantes sont simplement des points de données uniques dans vos données qui ne suivent pas le modèle habituel (par exemple,, dans une étude sur les scores de QI de 100 étudiants, où le score moyen était de 108 avec seulement une petite variation entre les étudiants, une étudiante avait un score de 156, ce qui est très inhabituel, et peut même la placer dans le top 1% des scores de QI à l’échelle mondiale). Les nuages de points suivants mettent en évidence l’impact potentiel des valeurs aberrantes:
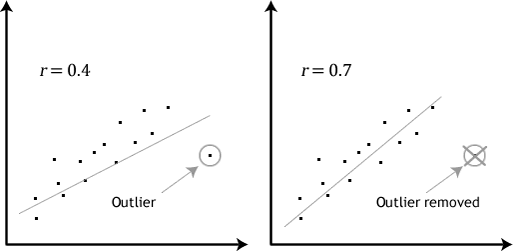
Le problème avec les valeurs aberrantes est qu’elles peuvent avoir un effet négatif sur l’équation de régression utilisée pour prédire la valeur de la variable dépendante en fonction de la variable indépendante., Cela modifiera la sortie produite par Stata et réduira la précision prédictive de vos résultats. Heureusement, vous pouvez utiliser Stata pour effectuer des diagnostics casewise pour vous aider à détecter d’éventuelles valeurs aberrantes.
- Hypothèse #5: Vous devriez avoir l’indépendance des observations, que vous pouvez facilement vérifier en utilisant la statistique de Durbin-Watson, qui est un test simple à exécuter en utilisant Stata.
- Hypothèse #6: Vos données doivent montrer l’homoscédasticité, c’est-à-dire où les variances le long de la ligne de meilleur ajustement restent similaires lorsque vous vous déplacez le long de la ligne., Les deux nuages de points ci-dessous fournissent des exemples simples de données qui répondent à cette hypothèse et qui échouent:
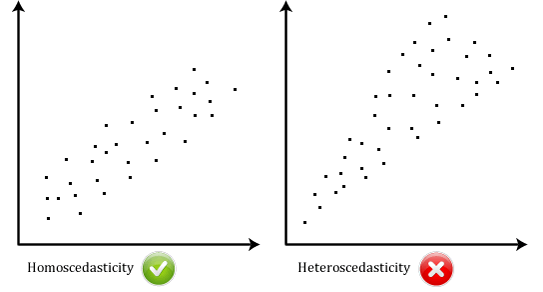
Lorsque vous analysez vos propres données, vous aurez de la chance si votre nuage de points ressemble à l’un des deux ci-dessus. Bien que ceux-ci aident à illustrer les différences dans les données qui répondent ou violent l’hypothèse de l’homoscédasticité, les données du monde réel sont souvent beaucoup plus désordonnées., Vous pouvez vérifier si vos données ont montré l’homoscédasticité en traçant les résidus normalisés de régression par rapport à la valeur prédite normalisée de régression.
- Hypothèse # 7: Enfin, vous devez vérifier que les résidus (erreurs) de la droite de régression sont approximativement normalement distribués. Deux méthodes courantes pour vérifier cette hypothèse comprennent l’utilisation d’un histogramme (avec une courbe normale superposée) ou d’un tracé P-P normal.
En pratique, vérifier les hypothèses #3, #4, #5, #6 et #7 prendra probablement la plupart de votre temps lors de la réalisation d’une régression linéaire., Cependant, il n’est pas une tâche difficile, et Stata fournit tous les outils dont vous avez besoin pour ce faire.
Dans la section, Procédure, nous illustrons la procédure Stata requise pour effectuer une régression linéaire en supposant qu’aucune hypothèse n’a été violée. Tout d’abord, nous présentons l’exemple que nous utilisons pour expliquer la procédure de régression linéaire dans Stata.
Stata
Exemple
les Études montrent que l’exercice peut aider à prévenir les maladies cardiaques. Dans des limites raisonnables, plus vous faites de l’exercice, moins vous risquez de souffrir d’une maladie cardiaque., Une façon dont l’exercice réduit votre risque de souffrir d’une maladie cardiaque est en réduisant une graisse dans votre sang, appelé cholestérol. Plus vous faites de l’exercice, plus votre concentration de cholestérol est faible. En outre, il a été récemment démontré que le temps que vous passez à regarder la télévision – un indicateur d’un mode de vie sédentaire – pourrait être un bon prédicteur de la maladie cardiaque (c.-à-d., plus vous regardez de télévision, plus votre risque de maladie cardiaque est élevé).,
Par conséquent, un chercheur a décidé de déterminer si la concentration de cholestérol était liée au temps passé à regarder la télévision chez des hommes de 45 à 65 ans en bonne santé (une catégorie de personnes à risque). Par exemple, comme les gens passaient plus de temps à regarder la télévision, leur concentration de cholestérol a-t-elle également augmenté (une relation positive); ou le contraire s’est-il produit? Le chercheur voulait également connaître la proportion de la concentration de cholestérol que le temps passé à regarder la télévision pourrait expliquer, ainsi que pouvoir prédire la concentration de cholestérol., Le chercheur pourrait alors déterminer si, par exemple, les personnes qui ont passé huit heures à regarder la télévision par jour avaient des niveaux dangereusement élevés de concentration de cholestérol par rapport aux personnes qui ne regardent que deux heures de télévision.
Pour réaliser l’analyse, le chercheur a recruté 100 participants masculins en bonne santé âgés de 45 à 65 ans. La quantité de temps passé à regarder la télévision (c.-à-d. la variable indépendante, time_tv) et la concentration de cholestérol (c.-à-d. la variable dépendante, cholestérol) ont été enregistrées pour les 100 participants., Exprimé en termes variables, le chercheur a voulu faire régresser le cholestérol sur time_tv.
Remarque: L’exemple et les données utilisées pour ce guide sont fictifs. Nous venons de créer pour les besoins de ce guide.
Stata
Configuration dans Stata
Remarque: Peu importe que vous créiez d’abord la variable dépendante ou indépendante.
Après avoir créé ces deux variables – time_tv et cholesterol-nous avons entré les scores pour chacune dans les deux colonnes de la feuille de calcul de l’éditeur de données (Edit) (c.-à-d.,, le temps en heures que les participants ont regardé la télévision dans la colonne de gauche (c’est-à-dire time_tv, la variable indépendante) et la concentration de cholestérol des participants en mmol/L dans la colonne de droite (c’est-à-dire cholestérol, la variable dépendante), comme indiqué ci – dessous:
Publié avec . ,
Stata
Procédure de test dans Stata
Dans cette section, nous vous montrons comment analyser vos données en utilisant la régression linéaire dans Stata lorsque les six hypothèses de la section précédente, Hypothèses, n’ont pas été violées. Vous pouvez effectuer une régression linéaire à l’aide de code ou de l’interface utilisateur graphique (GUI) de Stata. Après avoir effectué votre analyse, nous vous montrons comment interpréter vos résultats. Tout d’abord, choisissez si vous souhaitez utiliser le code ou l’interface utilisateur graphique (GUI) de Stata.,
Code
Le code pour effectuer une régression linéaire sur vos données prend la forme:
régressez DependentVariable IndependentVariable
Ce code est entré dans la case ci-dessous:
Publié avec l’autorisation écrite de StataCorp LP.,
En utilisant notre exemple où la variable dépendante est le cholestérol et la variable indépendante est time_tv, le code requis serait:
régression du cholestérol time_tv
Note 1: Vous devez être précis lorsque vous entrez le code dans la zone . Le code est « sensible à la casse ». Par exemple, si vous avez entré « Cholestérol » où le » C » est en majuscule plutôt qu’en minuscule (c’est-à-dire,, un petit « c »), ce qu’il devrait être, vous obtiendrez un message d’erreur comme suit:
Note 2: Si vous obtenez toujours le message d’erreur dans la Note 2: ci-dessus, il vaut la peine de vérifier le nom que vous avez donné à vos deux variables dans l’Éditeur de données lorsque vous configurez votre fichier (c’est-à-dire, voir l’écran de l’éditeur de données ci-dessus)., Dans la zone sur le côté droit de l’écran de l’éditeur de données, c’est la façon dont vous avez orthographié vos variables dans la section
, pas la section
que vous devez entrer dans le code (voir ci-dessous pour notre variable dépendante). Cela peut sembler évident, mais c’est une erreur qui est parfois commise, entraînant l’erreur de la note 2 ci-dessus.
Par conséquent, entrez le code, régressez cholestérol time_tv, et appuyez sur le bouton « Retour/Entrée » sur votre clavier.,
Publié avec la permission écrite de StataCorp LP.
Vous pouvez voir la sortie Stata qui sera produite ici.,
Interface utilisateur graphique (GUI)
Les trois étapes requises pour effectuer une régression linéaire dans Stata 12 et 13 sont présentées ci-dessous:
- Cliquez sur Statistiques > Modèles linéaires et connexes > Régression linéaire dans le menu principal, comme indiqué ci-dessous:
Publié avec l’autorisation écrite de StataCorp LP.,
La boîte de dialogue Régression – régression linéaire vous sera présentée:
Publiée avec l’autorisation écrite de StataCorp LP.
- Sélectionnez cholestérol dans la boîte déroulante Variable dépendante: et time_tv dans la boîte déroulante Variables indépendantes:. Vous obtiendrez l’écran suivant:
Publié avec la permission écrite de StataCorp LP.,
-
Cliquer sur le
le bouton. Cela générera la sortie.
Stata
Sortie de l’analyse de régression linéaire dans Stata
Si vos données ont passé l’hypothèse #3 (c.-à-d. qu’il y avait une relation linéaire entre vos deux variables), #4 (c.-à-d. qu’il n’y avait pas de valeurs aberrantes significatives), l’hypothèse # 5 (c.-à-c’est-à-dire,, les résidus (erreurs) étaient approximativement normalement distribués), ce que nous avons expliqué plus tôt dans la section Hypothèses, vous n’aurez besoin que d’interpréter la sortie de régression linéaire suivante dans Stata:
Publié avec l’autorisation écrite de StataCorp LP.,
La sortie se compose de quatre informations importantes: (a) la valeur R2 (ligne »R au carré ») représente la proportion de variance dans la variable dépendante qui peut être expliquée par notre variable indépendante (techniquement, c’est la proportion de variation prise en compte par le modèle de régression au-delà du modèle moyen). Cependant, R2 est basé sur l’échantillon et est positivement estimation biaisée de la proportion de la variance de la variable dépendante expliquée par le modèle de régression (c’est à dire,(c) la valeur F, les degrés de liberté (« F( 1, 98) ») et la signification statistique du modèle de régression (« Prob > F »); et (d) les coefficients de la variable constante et indépendante (« Coef. »colonne), qui est l’information dont vous avez besoin pour prédire la variable dépendante, cholestérol, en utilisant la variable indépendante, time_tv.
Dans cet exemple, R2 = 0.151. R2 ajusté = 0.143 (à 3 d.p.,), ce qui signifie que la variable indépendante, time_tv, explique 14,3% de la variabilité de la variable dépendante, le cholestérol dans la population. R2 ajusté est également une estimation de la taille de l’effet, qui, à 0,143 (14,3%), indique une taille d’effet moyenne, selon la classification de Cohen (1988). Cependant, normalement, c’est R2 et non le R2 ajusté qui est rapporté dans les résultats. Dans cet exemple, le modèle de régression est statistiquement significatif, F (1, 98) = 17,47, p = .0001., Cela indique que, dans l’ensemble, le modèle appliqué peut prédire statistiquement de manière significative la variable dépendante, le cholestérol.
Remarque: Nous présentons le résultat de l’analyse de régression linéaire ci-dessus. Cependant, puisque vous auriez dû tester vos données pour les hypothèses que nous avons expliquées plus haut dans la section Hypothèses, vous devrez également interpréter la sortie Stata qui a été produite lorsque vous avez testé pour ces hypothèses. Cela inclut: (a) les nuages de points que vous avez utilisés pour vérifier s’il y avait une relation linéaire entre vos deux variables (c’est-à-dire,(Hypothèse #3); (b) diagnostics casewise pour vérifier qu’il n’y avait pas de valeurs aberrantes significatives (Hypothèse #4); (c) la sortie de la statistique de Durbin-Watson pour vérifier l’indépendance des observations (Hypothèse #5); (d) un nuage de points des résidus normalisés de régression par rapport à la valeur prédite normalisée de régression pour déterminer si vos données les résidus (erreurs) étaient approximativement répartis normalement (c.-à-d. , hypothèse no 7)., De plus, n’oubliez pas que si vos données échouent à l’une de ces hypothèses, le résultat que vous obtenez de la procédure de régression linéaire (c’est-à-dire le résultat dont nous discutons ci-dessus) ne sera plus pertinent et vous devrez peut-être effectuer un test statistique différent pour analyser vos données.,
Stata
Déclaration de la sortie de l’analyse de régression linéaire
Lorsque vous déclarez la sortie de votre régression linéaire, il est recommandé d’inclure: (a) une introduction à l’analyse que vous avez effectuée; (b) des informations sur votre échantillon, y compris les valeurs manquantes; (c) la valeur F observée, les degrés de liberté et le niveau de signification (c.-à-d. la valeur p); (d) le pourcentage de la variabilité de la variable dépendante expliquée par la variable indépendante (c.-à-d., votre R2 ajusté ); et (e) l’équation de régression pour votre modèle., Sur la base des résultats ci-dessus, nous pourrions rapporter les résultats de cette étude comme suit:
- Général
Une régression linéaire a établi que le temps quotidien passé à regarder la télévision pouvait prédire statistiquement de manière significative la concentration de cholestérol, F(1, 98) = 17.47, p = .0001 et le temps passé à regarder la télévision représentaient 14,3% de la variabilité expliquée de la concentration de cholestérol. L’équation de régression était la suivante: concentration prévue de cholestérol = -2,135 + 0,044 x (temps passé à regarder la télévision).,
En plus du rapport sur les résultats ci-dessus, un schéma peut être utilisé pour la présentation visuelle des résultats. Par exemple, vous pouvez le faire en utilisant un nuage de points avec des intervalles de confiance et de prédiction (bien qu’il ne soit pas très courant d’ajouter le dernier). Cela peut faciliter la compréhension de vos résultats par les autres. De plus, vous pouvez utiliser votre équation de régression linéaire pour faire des prédictions sur la valeur de la variable dépendante en fonction de différentes valeurs de la variable indépendante., Bien que Stata ne produise pas ces valeurs dans le cadre de la procédure de régression linéaire ci-dessus, il existe une procédure dans Stata que vous pouvez utiliser pour le faire.