Calcul de l’aire sous une courbe.
Intégrales définies
Jusqu’à présent, lors de l’intégration, il reste toujours un terme constant. Pour cette raison, de telles intégrales sont appelées intégrales indéfinies. Avec des intégrales définies, nous intégrons une fonction entre 2 points, et ainsi nous pouvons trouver la valeur précise de l’intégrale et il n’y a pas besoin de termes constants inconnus .,

L’Aire Sous une Courbe
L’aire sous une courbe entre deux points peut être trouvée en faisant une intégrale entre les deux points.
Pour trouver l’aire sous la courbe y = f(x) entre x = a et x = b, d’intégrer y = f(x) entre les limites a et b.
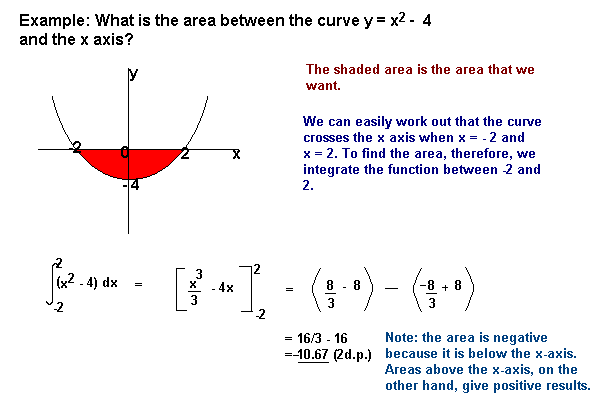
les Zones relevant de l’axe des x sortira le négatif et les zones au-dessus de l’axe des x positifs. Cela signifie que vous devez être prudent lorsque vous trouvez une zone qui est en partie au-dessus et en partie au-dessous de l’axe des abscisses.,
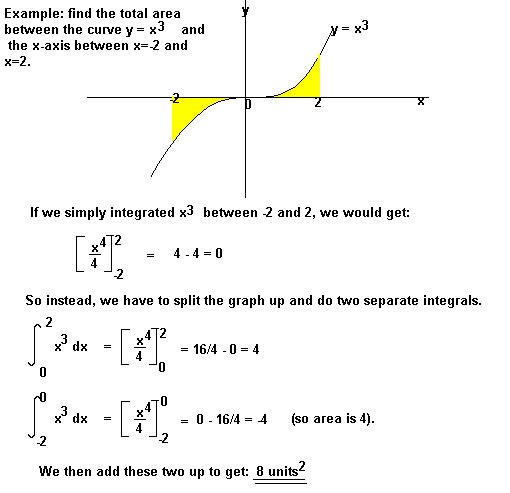
Vous pouvez également être invité à trouver l’aire entre la courbe et l’axe des ordonnées. Pour ce faire, intégrez par rapport à y.
Exemple
Recherchez la zone délimitée par les lignes y = 0, y = 1 et y = x2.