der Berechnung der Fläche unter einer Kurve.
Definite Integrale
Bisher war bei der Integration immer ein konstanter Begriff übrig. Aus diesem Grund werden solche Integrale als unbestimmte Integrale bezeichnet. Mit bestimmten Integralen integrieren wir eine Funktion zwischen 2 Punkten, sodass wir den genauen Wert des Integrals finden können und keine unbekannten konstanten Begriffe erforderlich sind .,

Die Fläche unter einer Kurve
Die Fläche unter einer Kurve zwischen zwei Punkten kann durch Ausführen eines bestimmten Integrals zwischen den beiden Punkten gefunden werden.
Um die Fläche unter der Kurve y = f(x) zwischen x = a und x = b zu finden, integrieren Sie y = f(x) zwischen den Grenzen von a und b.
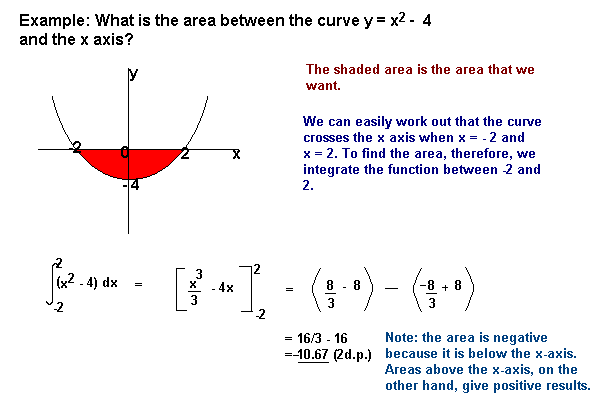
Bereiche unter der x-Achse werden negativ und Bereiche über der x-Achse positiv sein. Dies bedeutet, dass Sie vorsichtig sein müssen, wenn Sie einen Bereich finden, der teilweise über und teilweise unter der x-Achse liegt.,
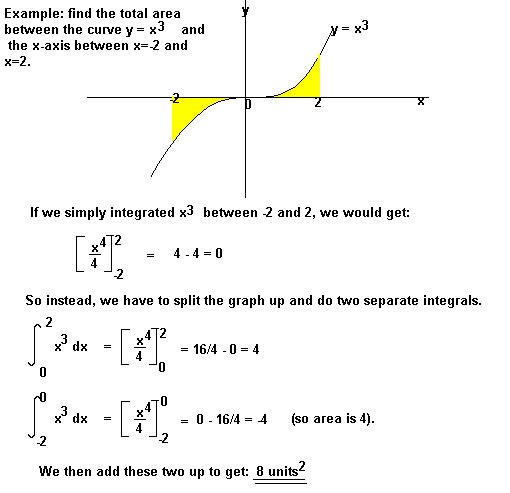
Möglicherweise werden Sie auch aufgefordert, den Bereich zwischen der Kurve und der y-Achse zu ermitteln. Integrieren Sie dazu in Bezug auf y.
Beispiel
Finden Sie den Bereich, der durch die Linien y = 0, y = 1 und y = x2 begrenzt ist.