Varianssi mittaa, kuinka paljon joukko tietoja on levinnyt ulos. Nollan varianssi osoittaa, että kaikki tietoarvot ovat identtisiä. Kaikki nollavarianssit ovat positiivisia.

pieni varianssi osoittaa, että datapisteet ovat yleensä hyvin lähellä keskimääräistä, ja toisiaan., Suuri varianssi osoittaa, että datapisteet ovat hyvin jakautuneet keskiarvosta ja toisistaan. Varianssi on neliömäisten etäisyyksien keskiarvo jokaisesta pisteestä keskiarvoon.

varianssin löytymisprosessi on hyvin samankaltainen kuin MAD: n, keskimääräisen absoluuttisen poikkeaman löytäminen.
ainoa ero on välimatkojen neliöiminen.
prosessi: (1) Etsi joukon keskiarvo (keskiarvo). (2) vähennä jokainen data-arvo keskiarvosta löytääksesi sen etäisyyden keskiarvosta. (3) neliö Kaikki etäisyydet. (4) Lisää kaikki neliöt etäisyydet., (4) Jaa tietojen lukumäärällä (populaatiovarianssille).

yksi varianssin ongelma on se, että sillä ei ole samaa mittayksikköä kuin alkuperäisillä tiedoilla. Esimerkiksi alkuperäisillä tiedoilla, jotka sisältävät jalkoina mitattuja pituuksia, on neliöjalkoina mitattu varianssi.,

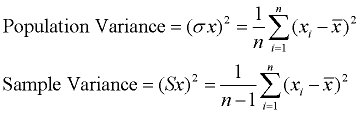Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Jos lasketaan käsin, on laskelmien sisällä aina enemmän desimaaleja kuin lopputuloksen odotetaan olevan. Jos työskentelet laskimen kanssa, kanna laskimen merkintöjen koko arvo, kunnes päädyt lopputulokseen.

keskihajonta osoittaa, kuinka paljon vaihtelua (hajonta, levittää, sironta) on siis olemassa., Se edustaa” tyypillistä ” poikkeamaa keskiarvosta. Se on suosittu vaihtelevuuden mitta, koska se palaa alkuperäisiin mittayksiköihin.

Pieni keskihajonta osoittaa, että datapisteet ovat yleensä hyvin lähellä keskimääräistä. Suuri keskihajonta osoittaa, että datapisteet jakautuvat laajalle arvovalikoimalle.
keskihajonta voi olla ajatellut kuin ”standardi” tapa tietää mikä on normaalia (tyypillinen), mikä on erittäin suuri, ja mikä on hyvin pieni tietokokonaisuus.,

keskihajonta on suosittu toimenpide vaihtelua, koska se palaa alkuperäiseen mittayksiköt tietojen joukko. Esimerkiksi jaloista mitattuja pituuksia sisältävissä alkuperäisissä tiedoissa on keskihajonta myös jaloista mitattuna.,

laskea keskihajonta käsin:
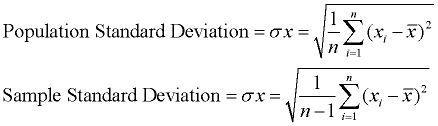keskihajonta on yksinkertaisesti neliöjuuri varianssi.
Tämä kuvaus koskee väestön keskihajontaa. Jos näytteen keskihajonta on tarpeen, JAA n: n sijasta N – 1: llä., Koska keskihajonta on varianssin neliöjuuri, meidän on ensin laskettava varianssi.
1. Etsi ilkeä.
2. Vähennä keskiarvo jokaisesta data-arvosta ja neliö kunkin näistä eroista (neliölliset erot).
3. Etsi keskimääräinen potenssiin eroja (lisää ne ja jaa count data-arvot). Tämä on varianssi.,

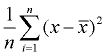vaihtelu
4. Ota neliöjuuri. Tämä on väestön keskihajonta. Kierrä vastaus ongelman ohjeiden mukaan.

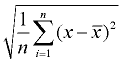keskihajonta

Normaali Käyrä

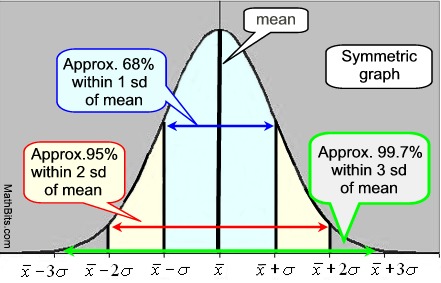
normaali käyrä on symmetrinen, bell-muotoinen käyrä., Kuvaajan keskipiste on keskiarvo, ja kuvaajan korkeus ja leveys määritetään keskihajonnan perusteella. Kun keskihajonta on pieni, käyrä on pitkä ja kapea leviäminen. Kun keskihajonta on suuri, käyrä on lyhyt ja leveä levitettynä. Keskiarvolla ja mediaanilla on sama arvo normaalikäyrässä.

Normaali Käyrä Empiirinen Sääntö:
Noin …

• * 68% tiedoista on yhden keskihajonnan sisällä.,

• * 95% tiedoista on kahden keskihajonnan sisällä.

• 99, 7% tiedoista on kolmen keskihajonnan sisällä.

IQR normaalikäyrällä on 1,34896 x keskihajonta.