Oletus normaaliuden riippuva muuttuja
riippumaton t-testi edellyttää, että riippuva muuttuja on likimain normaalisti jakautunut kunkin ryhmän sisällä.
huomaa: teknisesti juuri residuaalit pitää jakaa normaalisti, mutta itsenäistä t-testiä varten molemmat antavat saman tuloksen.,
Voit testata tämän käyttämällä useita eri testejä, mutta Shapiro-Wilks-testi normaaliuden tai graafinen menetelmä, kuten Q-Q Plot, ovat hyvin yleisiä. Voit suorittaa nämä testit käyttämällä SPSS tilastoja, menettely, joka löytyy meidän testaus normaalius opas. T-testiä kuvataan kuitenkin vakaaksi testiksi normaaliuden olettamisen suhteen. Tämä tarkoittaa, että jollain poikkeamisella normaaliudesta ei ole suurta vaikutusta tyypin I virhetasoihin. Poikkeuksena tähän on, jos pienimmän ja suurimman ryhmäkoon suhde on suurempi kuin 1.,5 (suurin verrattuna pienimpään).
Mitä tehdä, kun rikot normaaliuden oletus
Jos huomaat, että joko yksi tai molemmat-ryhmän tietoja ei noin normaalisti jakautunut ja ryhmien koot vaihtelevat suuresti, sinulla on kaksi vaihtoehtoa: (1) muuntaa tiedot niin, että tiedot tulee normaalisti jakautunut (voit tehdä tämän SPSS Statistics katso oppaamme Muuttamassa Tiedot), tai (2) suorita Mann-Whitney U-testillä, joka on ei-parametrinen testi, joka ei vaadi oletusta normaaliuden (suorita tämä testi SPSS Statistics katso oppaamme Mann-Whitney U-Testi).,
Oletus homogeenisuudesta varianssi
riippumaton t-testi olettaa, että näiden kahden ryhmän varianssit olet mittaaminen ovat yhtä väestöstä. Jos varianssisi ovat epätasa-arvoisia, tämä voi vaikuttaa tyypin I virhetasoon. Oletus varianssin homogeenisuudesta voidaan testata Levenen Varianssitestillä, joka tuotetaan SPSS: n tilastoissa riippumattoman t-testimenettelyn aikana., Jos sinulla on ajaa Levene ’ s Test of Equality of Varianssit SPSS Statistics, saat tuloksen samanlainen kuin alla:

Tämä testi homogeenisuus varianssi tarjoaa F-arvo ja merkitsevyys arvo (p-arvo). Olemme ensisijaisesti merkitys-arvo – jos se on suurempi kuin 0,05 (eli p > .05), ryhmämme variansseja voidaan kohdella tasavertaisina. Kuitenkin, jos p < 0.05, meillä on epätasa-arvoinen varianssit ja meillä on rikkonut oletus varianssien homogeenisuus.,
Voittaminen rikkoo oletus homogeenisuudesta varianssi
Jos Levene ’ s Test for Equality of Varianssit on tilastollisesti merkittävä, mikä osoittaa, että ryhmä varianssit ovat erisuuruiset väestön, voit korjata tätä vastoin ei käyttäen yhdistettyjä arvio virhetermi t-statistic, mutta sen sijaan käyttää mukauttamista vapausasteita käyttämällä Welch-Satterthwaite-menetelmällä., Todellisuudessa, sinun ei luultavasti koskaan kuullut näitä muutoksia, koska SPSS Tilasto piilottaa nämä tiedot, ja yksinkertaisesti tarrat kaksi vaihtoehtoa, kuten ”Tasa-varianssit olettaa” ja ”Yhtäläisten varianssien ei oleteta” ilman selkeästi taustalla testejä käytetään., Kuitenkin, voit nähdä todisteet näistä testeistä, kuten alla:
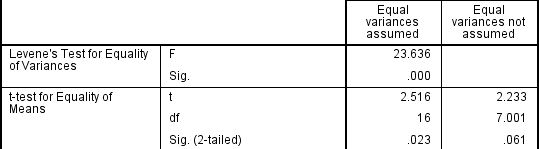
tulos Levene ’ s Test for Equality of Varianssit, emme voi hylätä nollahypoteesia, että ei ole eroa varianssit ryhmien välillä ja hyväksyä vaihtoehtoinen hypoteesi, joka on tilastollisesti merkittävä ero varianssit ryhmien välillä., Vaikutus ei voi olettaa yhtä vaihtelut on nähtävissä viimeisessä sarakkeessa mainittu luku, jossa näemme vähentäminen-arvo t-arvo ja suuri väheneminen vapausasteet (df). Tämä nostaa p-arvoa yli kriittisen merkitsevyystason 0,05. Tässä tapauksessa, emme siis hyväksy vaihtoehtoinen hypoteesi ja hyväksyä, että ei ole tilastollisesti merkittäviä eroja tarkoittaa. Tämä ei olisi ollut meidän päätelmämme, ellemme olisi testanneet varianssien homogeenisuutta.