Johdanto
Lineaarinen regressio, joka tunnetaan myös nimellä yksinkertainen lineaarinen regressio tai kahden muuttujan lineaarinen regressio, käytetään, kun halutaan ennustaa arvon riippuvan muuttujan arvon perusteella riippumaton muuttuja. Lineaarisen regression avulla voisi esimerkiksi ymmärtää, voidaanko kokeen suoritus ennustaa revisioajan perusteella (ts., sinun riippuva muuttuja olisi ”tentti suorituskykyä”, mitattu 0-100 markkaa, ja riippumaton muuttuja olisi ”tarkistamista aikaa”, mitattu tuntia). Vaihtoehtoisesti, voit käyttää lineaarinen regressio ymmärtää, onko savukkeiden kulutusta voidaan ennustaa sen perusteella, tupakoinnin kesto (eli oman riippuva muuttuja olisi ”savukkeiden kulutusta”, mitattuna savukkeiden määrä kulutetaan päivittäin, ja riippumaton muuttuja olisi ”tupakoinnin kesto”, mitattuna päivää). Jos sinulla on kaksi tai enemmän riippumattomia muuttujia, eikä vain yksi, sinun täytyy käyttää useita regressio., Vaihtoehtoisesti, jos haluat vain selvittää, onko lineaarinen yhteys on olemassa, voit käyttää Pearsonin korrelaatio.
Huomautus: riippuva muuttuja on myös nimitystä tulos, kohde-tai kriteeri muuttuja, kun riippumaton muuttuja on myös nimitystä predictor, selittävä tai regressor muuttuja. Lopulta, kumpi termi käytät, se on parasta olla johdonmukainen. Viittaamme näihin riippuvina ja riippumattomina muuttujina tässä oppaassa.,
tässä oppaassa, näytämme, miten suorittaa lineaarinen regressio käyttäen Stata, sekä tulkita ja raportoida tuloksia tässä testissä. Kuitenkin, ennen kuin esittelemme sinut tähän menettelyyn, sinun täytyy ymmärtää erilaisia oletuksia, että tietosi on täytettävä, jotta lineaarinen regressio antaa sinulle kelvollisen tuloksen. Seuraavaksi keskustelemme näistä oletuksista.
Stata
Oletukset
On olemassa seitsemän ”oletukset”, jotka tukevat lineaarinen regressio. Jos jokin näistä seitsemästä oletuksesta ei täyty, et voi analysoida tietojasi lineaarisesti, koska et saa pätevää tulosta., Koska oletukset #1 ja #2 liittyvät teidän valinta muuttujia, niitä ei voida testata käyttäen Stata. Sinun pitäisi kuitenkin päättää, vastaako tutkimuksesi näitä oletuksia ennen kuin siirryt eteenpäin.
- oletus #1: riippuvainen muuttuja on mitattava jatkuvalla tasolla., Esimerkkejä tällaisista jatkuvia muuttujia ovat korkeus (mitattuna jalkaa ja tuumaa), lämpötila (mitattuna oC), palkka (mitattuna YHDYSVALTAIN dollareissa), tarkistus-aika (mitattu tuntia), älykkyys (mitattu ÄO-pisteet), reaktioaika (mitataan millisekunteina), testi suorituskyky (mitattuna 0: sta 100), myynti (mitattuna määrä liiketoimia kuukaudessa), ja niin edelleen. Jos olet epävarma siitä, onko riippuvainen muuttuja jatkuva (eli mitattuna intervalli-tai suhdetasolla), katso vaihtuva oppaamme.,
- oletus #2: itsenäinen muuttuja on mitattava jatkuvalla tai kategorisella tasolla. Kuitenkin, jos sinulla on kategorinen riippumaton muuttuja, se on yleisempää käyttää riippumaton t-testi (2 ryhmää) tai yksisuuntaisella ANOVA (3 ryhmää tai enemmän). Jos olet epävarma, esimerkkejä kategorisia muuttujia ovat sukupuoli (esim., 2 ryhmää: uros ja naaras), etnisyys (esim., 3 ryhmää: Valkoihoinen, Afrikkalainen Amerikan ja Hispanic), fyysisen aktiivisuuden taso (esim., 4 ryhmää: istumista, matala, kohtalainen ja korkea), ja ammatti (esim.,, 5 ryhmää: kirurgi, lääkäri, sairaanhoitaja, hammaslääkäri, terapeutti). Tässä oppaassa, näytämme, lineaarinen regressio menettely ja Stata lähtö, kun molemmat riippuvaisia ja riippumattomia muuttujia mitattiin jatkuvalla tasolla.
Onneksi, voit tarkistaa oletuksia #3, #4, #5, #6 ja #7 käyttäen Stata. Kun siirrytään oletukset #3, #4, #5, #6 ja #7, suosittelemme, testata niitä tässä järjestyksessä, koska se edustaa tilaa, jossa, jos vastoin oletusta ei ole korjattavissa, et enää voi käyttää lineaarinen regressio., Itse asiassa, älä ihmettele, jos tietoja ei yksi tai useampi näistä oletukset, koska tämä on melko tyypillinen, kun työskennellään todellisten tietojen sijaan oppikirja esimerkkejä, jotka usein vain näyttää, miten suorittaa lineaarinen regressio kun kaikki menee hyvin. Kuitenkin, älä huoli, koska jopa silloin, kun tietoja ei tiettyjä oletuksia, on usein ratkaisu voittaa (esim, muuttaa tietojasi tai käyttää toista tilastollinen testi sen sijaan)., Vain muistaa, että jos et tarkista, että tiedot täyttävät nämä oletukset tai testata niitä väärin, tulokset saat, kun käynnissä lineaarinen regressio ei ehkä ole voimassa.
- Oletus #3: On oltava lineaarisesti riippuvat ja riippumattomat muuttujat. Vaikka on olemassa useita tapoja tarkistaa, onko lineaarinen suhde välillä teidän kaksi muuttujaa, suosittelemme luomaan scatterplot käyttäen Stata, jossa voit juoni riippuva muuttuja vastaan riippumaton muuttuja., Voit sitten visuaalisesti tarkastaa scatterplot tarkistaa lineaarisuus. Sinun scatterplot voi näyttää yhden seuraavista:
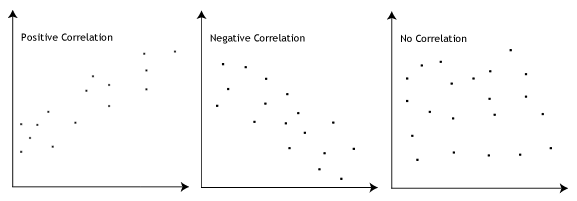
Jos suhde näytetään scatterplot ei ole lineaarinen, sinun täytyy joko ajaa ei-lineaarinen regressio-analyysi tai ”muuttaa” sinun tiedot, jotka voit tehdä käyttämällä Stata.
- oletus #4: merkittäviä poikkeamia ei pitäisi olla. Poikkeamat ovat vain yksittäisiä datapisteitä, jotka eivät noudata tavanomaista kaavaa (esim., tutkimuksessa 100 opiskelijoiden IQ tulokset, jossa keskimääräinen pistemäärä oli 108 ja vain pieni vaihtelu opiskelijoiden välillä, yksi opiskelija oli pisteet 156, joka on hyvin epätavallista, ja voi jopa laittaa hänen top 1% IQ tulokset maailmanlaajuisesti). Seuraavat scatterplots korostaa mahdollisia vaikutuksia harha:
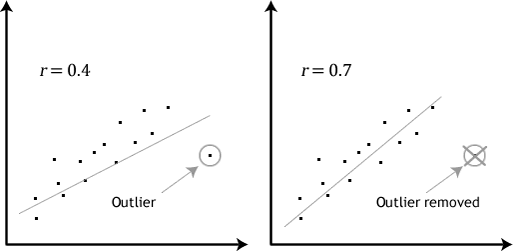
ongelma harha on, että ne voivat olla negatiivinen vaikutus regressioyhtälö, jota käytetään ennustaa arvo riippuva muuttuja perustuu riippumattoman muuttujan., Tämä muuttaa statan tuottamaa ulostuloa ja vähentää tulosten ennakoivaa tarkkuutta. Onneksi voit käyttää Stata tehdä casewise diagnostiikka auttaa havaitsemaan mahdolliset poikkeamat.
- Oletus #5: Sinun pitäisi olla riippumattomuuden havainnoista, jotka voit helposti tarkistaa käyttämällä Durbin-Watson statistic, joka on yksinkertainen testi ajaa käyttäen Stata.
- oletus #6: tietojesi on näytettävä homosedastisuus, jossa parhaan istuvuuden linjan varianssit pysyvät samanlaisina, kun liikut linjaa pitkin., Kaksi scatterplots alla tarjota yksinkertaisia esimerkkejä data, joka täyttää tämän oletuksen ja yksi, että ei oletus:
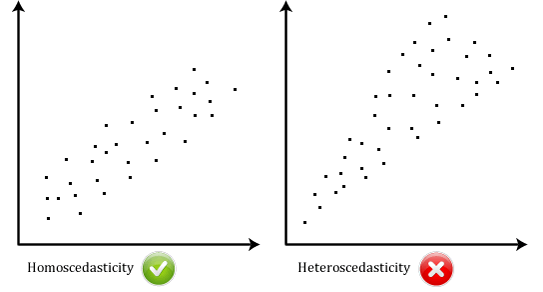
Kun analysoida omia tietoja, voit olla onnekas, jos scatterplot näyttää joko kaksi edellä. Vaikka nämä auttavat havainnollistamaan eroja data, joka täyttää tai rikkoo oletus homoscedasticity, real-world data on usein paljon enemmän sotkuinen., Voit tarkistaa, osoittivatko tietosi homosedastisuutta piirtämällä regression standardoidut residuaalit regression standardoitua ennustettua arvoa vastaan.
- oletus #7: lopuksi on tarkistettava, että regressiolinjan residuaalit (virheet) jakautuvat suunnilleen normaalisti. Kaksi yleistä menetelmää tämän oletuksen tarkistamiseksi ovat joko histogrammi (jossa on päällekkäinen normaali käyrä) tai normaali P-P-juoni.
käytännössä oletusten tarkistaminen #3, #4, #5, #6 ja #7 luultavasti vie suurimman osan ajastasi suorittaessaan lineaarista regressiota., Se ei kuitenkaan ole vaikea tehtävä, ja Stata tarjoaa kaikki tarvittavat työkalut tähän.
jaksossa, menettelyssä, havainnollistamme lineaarisen regression suorittamiseen vaadittavaa Stata-menettelyä olettaen, ettei oletuksia ole rikottu. Ensinnäkin esitämme esimerkin, jota käytämme selittämään lineaarista regressiomenettelyä Statassa.
Stata
Esimerkki
Tutkimukset osoittavat, että käyttäessään voi auttaa ehkäisemään sydänsairauksia. Kohtuullisissa rajoissa, enemmän liikut, sitä pienempi riski sinulla on sairastua sydänsairauksiin., Yksi tapa, jolla liikunta vähentää riskiä sairastua sydän tauti on vähentämällä rasvaa veressä, kutsutaan kolesterolin. Mitä enemmän liikut, sitä pienempi on kolesterolipitoisuus. Lisäksi se on äskettäin osoitettu, että aikaa vietät TELEVISION katselun – indikaattori liikunnan puute – voisi olla hyvä ennustaja sydänsairaus (eli, että on, enemmän TV voit katsella, sitä suurempi sydänsairauksien riskiä).,
näin Ollen tutkija päätti selvittää, jos kolesterolin pitoisuus liittyi aikaa viettänyt katsellen TV-muuten terve 45-65 vuotiaat miehet (at-risk ryhmä ihmisiä). Esimerkiksi kun ihmiset käyttivät enemmän aikaa television katseluun, lisääntyikö heidän kolesterolipitoisuutensa (positiivinen suhde) vai tapahtuiko päinvastoin? Tutkija halusi myös tietää, osuus-kolesterolin pitoisuus, joka vietti aikaa TELEVISION katselun voisi selittää, sekä pysty ennustamaan kolesterolin pitoisuus., Tutkija voisi selvittää, onko esimerkiksi ihmiset, jotka vietti kahdeksan tuntia viettänyt katsellen TV-päivässä oli vaarallisen korkea kolesteroli pitoisuus verrattuna ihmisiä katsomassa vain kaksi tuntia TV: tä.
analyysiä varten tutkija värväsi 100 tervettä 45-65-vuotiasta miespuolista osallistujaa. Aikaa kuluu TELEVISION katselun (eli riippumaton muuttuja, time_tv) ja kolesterolin pitoisuus (eli riippuva muuttuja, kolesteroli) kirjattiin kaikki 100 osallistujaa., Ilmaistaan muuttujan kannalta, tutkija halusi taantua kolesteroli time_tv.
huomaa: tässä oppaassa käytetty esimerkki ja tiedot ovat kuvitteellisia. Olemme juuri luoneet ne tämän oppaan tarkoitusta varten.
Stata
Setup Stata
Huomaa: Se ei ole väliä, onko voit luoda riippuvainen tai riippumaton muuttuja ensin.
Kun olet luonut nämä kaksi muuttujaa – time_tv ja kolesteroli – olemme tulleet tulokset kunkin osaksi kaksi saraketta Data Editor (Muokata) taulukkolaskenta (ts., aika tunteina, että osallistujat katseli TV vasemmassa sarakkeessa (eli time_tv, riippumaton muuttuja), ja osallistujien kolesterolin pitoisuus mmol/L oikeanpuoleinen sarake (ts, kolesteroli, riippuva muuttuja), kuten alla:
Julkaistu kirjallista lupaa StataCorp LP.,
Stata
testausmenettely Stata
tässä osassa, näytämme, miten analysoida tietoja käyttämällä lineaarinen regressio Stata, kun kuusi oletukset edellisessä jaksossa, Oletukset, ei ole rikottu. Voit suorittaa lineaarisen regression käyttämällä koodia tai Statan graafista käyttöliittymää (GUI). Kun olet tehnyt analyysisi, näytämme, miten voit tulkita tuloksiasi. Valitse ensin, haluatko käyttää koodia vai Statan graafista käyttöliittymää (GUI).,
Koodi
koodi suorittaa lineaarinen regressio tietoja muodossa:
taantua DependentVariable IndependentVariable
Tämä koodi on syötetty laatikko alla:
Julkaistu kirjallista lupaa StataCorp LP.,
Käyttämällä esimerkiksi silloin, kun riippuva muuttuja on kolesteroli-ja riippumaton muuttuja on time_tv, tarvittava koodi olisi:
taantua kolesteroli time_tv
Huomautus 1: Sinun täytyy olla tarkka, kun syötät koodi laatikko. Koodi on ”case sensitive”. Esimerkiksi, jos olet tullut ”kolesteroli”, jossa ” C ” on suuraakkosena sijaan lowercase (ts., pieni ”c”), jossa sen pitäisi olla, saat virheilmoituksen, kuten seuraavat:
Huomautus 2: Jos olet edelleen saada virhe viesti Huomautus 2: edellä mainitut, on syytä tarkistaa antamasi nimen omaan kahden muuttujan Data editor, kun olet määrittänyt tiedoston (eli katso Data Editor-näyttö.edellä)., laatikko oikealla puolella Data Editor-näyttö, se on tapa, että olet kirjoitettu muuttujien
– osioon
kohta, että sinun täytyy syöttää koodi (katso alla meidän riippuva muuttuja). Tämä voi tuntua ilmeiseltä, mutta se on virhe, joka joskus tehdään, jolloin virhe huomautuksessa 2 edellä.
näin Ollen, anna koodi, taantua kolesteroli time_tv, ja paina ”Return/Enter” – painiketta näppäimistön.,
Julkaistu kirjallista lupaa StataCorp LP.
voit katsoa Stata-lähdön, joka tuotetaan täällä.,
Graafinen Käyttöliittymä (GUI)
kolme vaihetta suoritettava lineaarinen regressio Stata 12 ja 13 on esitetty alla:
- Klikkaa Tilastot > Lineaariset mallit ja niihin liittyvät > Lineaarinen regressio päävalikossa, kuten alla:
Julkaistu kirjallista lupaa StataCorp LP.,
Sinulle esitetään kanssa Taantua – Lineaarinen regressio-valintaikkuna:
Julkaistu kirjallista lupaa StataCorp LP.
- Valitse kolesterolia sisällä Riippuva muuttuja: drop-alas ruutuun ja time_tv sisällä Riippumattomia muuttujia: drop-alas ruutuun. Voit päätyä seuraava näyttö:
Julkaistu kirjallista lupaa StataCorp LP.,
-
Klikkaa
– painiketta. Tämä luo tuotoksen.
Stata
Lähtö lineaarinen regressio analyysi Stata
Jos tiedot välitetään oletus #3 (eli siellä oli lineaarinen suhde teidän kahden muuttujan), #4 (eli ei ollut merkittäviä outliers), olettaen, #5 (toisin sanoen, teillä oli itsenäisyyttä havaintoja), olettaen, #6 (eli oman tiedot osoittivat homoscedasticity) ja olettaen, #7 (ts.,, residuaalit (virheet) olivat likimain normaalisti jakautunut), jossa selitimme aiemmin Oletukset-osiossa, sinun tarvitsee vain tulkita seuraavasti lineaarinen regressio lähtö Stata:
Julkaistu kirjallista lupaa StataCorp LP.,
lähtö koostuu neljästä tärkeitä tietoja: (a) R2 arvo (”R-squared” rivi) edustaa osuus varianssi riippuvainen muuttuja, joka voidaan selittää meidän riippumaton muuttuja (teknisesti se on osa vaihtelusta selittyy regressiomallin ylä-ja ulkopuolella siis malli). Kuitenkin, R2 perustuu otokseen, ja on suorastaan puolueellinen arvio osuus varianssi riippuva muuttuja selittyy regressiomallin (ts., se on liian suuri); (b) korjattu R2 arvo (”Adj R-squared” rivi), joka korjaa positiivinen bias tarjoamaan arvoa, joka olisi odotettavissa väestöstä; (c) F-arvo, vapausasteet (”F( 1, 98)”) ja tilastollinen merkitsevyys regressiomalli (”Prob > F” rivi); ja (d) kertoimia vakio ja riippumaton muuttuja (”Coef.”sarake), joka on tieto, joka sinun täytyy ennustaa riippuvainen muuttuja, kolesteroli, käyttäen riippumattoman muuttujan, time_tv.
tässä esimerkissä R2 = 0, 151. Korjattu R2 = 0,143 (arvoon 3 D.p.,), mikä tarkoittaa, että riippumaton muuttuja, time_tv, kertoo 14.3% vaihtelun riippuvan muuttujan, kolesteroli, väestöstä. Oikaistu R2 on myös arvio vaikutus koko, joka on 0,143 (14.3%), on osoitus keskipitkän vaikutus koko, mukaan Cohenin (1988) luokitus. Tavallisesti tuloksissa ei kuitenkaan ilmoiteta korjattua R2-arvoa. Tässä esimerkissä regressiomalli on tilastollisesti merkitsevä, F(1, 98) = 17.47, p = .0001., Tämä osoittaa, että yleisesti käytetty malli voi tilastollisesti merkittävästi ennustaa riippuvainen muuttuja, kolesteroli.
Huomautus: esittelemme lähtö lineaarinen regressioanalyysi edellä. Kuitenkin, koska sinun olisi pitänyt testata tietojasi oletukset selitimme aiemmin Oletukset-osiossa, sinun täytyy myös tulkita Stata tuotos, joka on tuotettu, kun testataan näitä oletuksia. Tämä sisältää: A) scatterplots käytit tarkistaa, jos oli lineaarinen suhde teidän kaksi muuttujaa (ts.,, Oletus #3); (b) casewise diagnostics tarkistaa, ei ollut merkittäviä poikkeavuuksia (eli Olettaen, #4); (c) lähtö Durbin-Watson statistic tarkistaa riippumattomuus havaintoja (eli Olettaen, #5); (d) scatterplot regressio standardoitujen jäännösten vastaan regressio standardoitu ennustettu arvo määrittää, onko tiedot osoittivat homoscedasticity (eli Olettaen, #6); ja histogrammi (kanssa päällekkäin normaali käyrä) ja Normal P-P Plot tarkistaa, onko jäännösten (virheet) olivat likimain normaalisti jakautunut (eli Olettaen, #7)., Muista myös, että jos data ei mitään näistä oletuksista, lähtö että voit saada lineaarinen regressio menettely (ts, lähtö keskustelemme edellä) ei ole enää merkitystä, ja saatat joutua suorittamaan eri tilastollinen testi analysoida tietoja.,
Stata
Raportointi lähtö lineaarinen regressioanalyysi
raportti tuotoksen teidän lineaarinen regressio, se on hyvä käytäntö ovat: (a) johdatus analyysi suoritetaan; (b) tietoa otoksesta, mukaan lukien kaikki puuttuvat arvot; (c) havaittu F-arvo, vapausasteet ja merkitsevyystaso (eli p-arvo); (d) prosenttiosuus vaihtelee riippuva muuttuja selittää riippumattoman muuttujan (eli oman Oikaistu R2 ); ja (e) regressio-yhtälön malli., Tulosten perusteella edellä, voimme raportoida tämän tutkimuksen tulokset seuraavasti:
- Yleistä
lineaarinen regressio todettiin, että päivittäin vietetty aika TELEVISION katselun voisi tilastollisesti merkitsevästi ennustavat kolesterolin pitoisuus, F(1, 98) = 17.47, p = .0001 ja television katseluun käytetty aika oli 14,3% selitetystä kolesterolipitoisuuden vaihtelusta. Regressioyhtälö oli: ennustettu kolesterolipitoisuus = -2,135 + 0,044 x (television katseluun käytetty aika).,
lisäksi tulosten raportointi kuten edellä, kaavio voidaan visuaalisesti esittää tulokset. Esimerkiksi, voit tehdä tämän käyttämällä scatterplot luottamusta ja ennustaminen välein (vaikka se ei ole kovin yleinen lisätä viimeinen). Tämä voi helpottaa muiden tulosten ymmärtämistä. Lisäksi voit tehdä lineaarisen regressioyhtälön avulla ennusteita riippuvan muuttujan arvosta riippumattoman muuttujan eri arvojen perusteella., Vaikka Stata ei tuota näitä arvoja osana lineaarinen regressio menettely edellä, on menettely, Stata, että voit tehdä niin.