Tämä on ensimmäinen kolme post-sarja. Toinen viesti puhuu siitä laskea Iso-O. kolmas artikkeli kertoo understandingthe virallista määritelmää Iso-O.
Iso-O-notaatio käytetään olla todella pelottava käsite minulle. Näin ”oikeat” ohjelmoijat puhuivat koodistaan. Se oli kaikki themore pelottava, koska akateemiset kuvaukset (kuten Wikipedia) madeeverely vähän järkeä minulle. Tämä on turhauttavaa, koska alivoimakäsitykset eivät oikeastaan ole niin vaikeita.,
yksinkertaisesti sanottuna, Big-O notaatio on se, miten ohjelmoijat puhuvat algoritmeista. Algoritmit ovat toinen pelottava aihe, joka suojaan toisessa viestissä, mutta meidän tarkoituksiin, sanotaan, että ”algoritmi” tarkoittaa afunction ohjelma (joka ei ole liian kaukana). Funktion Iso-Onotaatio määräytyy sen mukaan, miten se reagoi eri tuloihin. Kuinka hitaampaa se on, jos annamme sille listan 1000 asioista, jotka toimivat 1 asian listalla?
Harkitse tätä koodia:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Joten jos me kutsumme tätä toimintoa, kuten item_in_list(2, ), se olisi melko nopeasti., Me silmukka jokaisen asian luettelossa ja jos me löytääensimmäinen argumentti tehtäväämme, palaa totta. Jos pääsemme loppuun, emmekä löytäneet sitä, palauta se vääränä.
tämän funktion ”monimutkaisuus” on O(n). Selitän, mitä tämä tarkoittaa, mutta puretaan tämä mathematicalsyntax. O(n) luetaan ”Order of N”, koska O toiminto on alsoknown kuin Tilaus toiminnon. Luulen, että tämä johtuu siitä, että teemme approksimaatiota, joka käsittelee ”suuruusluokkaa”.,
”suuruusluokat” on jälleen yksi matemaattinen termi, joka kertoo matemaattisesti lukujen luokkien välisen eron. Ajattele eroa välillä 10 ja 100. Jos kuvittelet 10 läheistä ystävääsi ja 100 ihmistä, se on todella iso ero. Samoin, thedifference välillä 1000 ja 10 000 on aika iso (itse asiassa, sen thedifference välillä junker auton ja kevyesti käyttää yksi). On käynyt ilmi, että approksimaatiossa, niin kauan kuin olet suuruusluokan sisällä, olet melko lähellä., Jos olet arvata määrää purkkapalloja vuonna amachine, olisit sisällä kertaluokkaa jos sanoi 200gumballs. 10 000 gumballia olisi kaukana.

Kuva 1: gumball kone, jonka määrä purkkapalloja on luultavasti sisällä suuruusluokkaa 200.
Takaisin dissecting O(n) tämä sanoo, että jos me piirtää aikaanse kestää suorittaa tämän toiminnon kanssa eri kokoinen tuotantopanosten (esim. anarray 1 tuote 2 erät, 3 tuotteet, jne), näemme, että itapproximately vastaa kohteiden määrä array., Tämä on lineaarinen kaavio. Tämä tarkoittaa, että linja on periaatteessa straightf sinun piti kuvaajaksi.
jotkut teistä ovat saattaneet huomata, että jos yllä olevassa koodinäytteessä ouritem oli aina listan ensimmäinen kohde, koodimme olisi reallyfast! Tämä on totta, mutta Big-O on kyse likimääräinen huonoin-caseperformance tehdä jotain. Pahimmassa tapauksessa koodi edellä on, että asia, jota etsimme ei ole luettelossa ollenkaan. (Huomautus:matemaattinen termi tämä on ”upper bound”, joka tarkoittaa sen puhumista mathematic raja awfulness).,
Jos haluat nähdä kaavion näitä toimintoja, sinun sivuuttaa O()toiminto ja muuttaa muuttujan n for x. Voit sitten kirjoittaa thatinto Wolfram Alpha kuin ”juoni x”, joka näyttää lävistäjä. Syy, miksi et vaihtaa pois n x on, että niiden kuvaajien programwants x sen muuttujan nimi, koska se vastaa xaxis. X-akseli kasvaa vasemmalta oikealle vastaa togiving isompi ja isompi paneelit teidän toiminnon., Y-axis edustaa aikaa, joten mitä korkeampi viiva, sitä hitaampi se on.
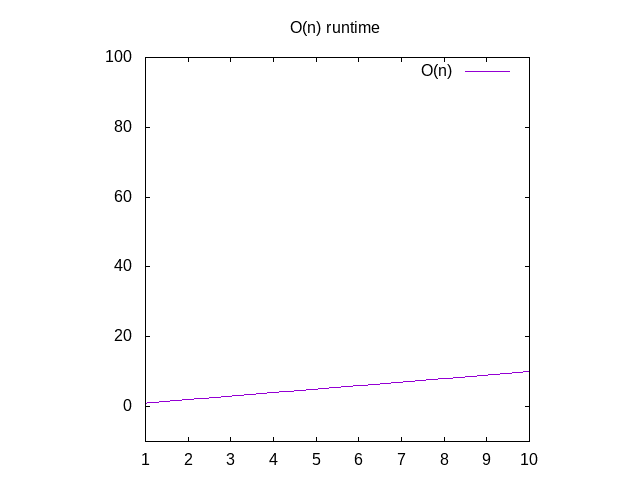
Kuva 2: Runtime ominaisuudet O(n) – funktio,
mitkä ovat joitakin muita esimerkkejä?
Harkitse tämän toiminnon:
def is_none(item): return item is None
Tämä on vähän hassu esimerkki, mutta vastaa minulle. Tätä funktiota kutsutaan O(1), jota kutsutaan ”vakioajaksi”. Mitä tämä tarkoittaa on nomatter kuinka suuri panos on, se vaatii aina saman verran aikaa laskea asioita., Jos menet takaisin Wolfram plot 1, saat sitten se pysyy aina samana, ei väliä kuinka pitkälle oikein mennään. Jos youpass luettelossa 1 miljoonaa kokonaislukua, se kestää suunnilleen saman ajan, jos olit menossa läpi luettelon 1 kokonaisluku. Vakioaikaa pidetään parhaana skenaariona funktiolle.
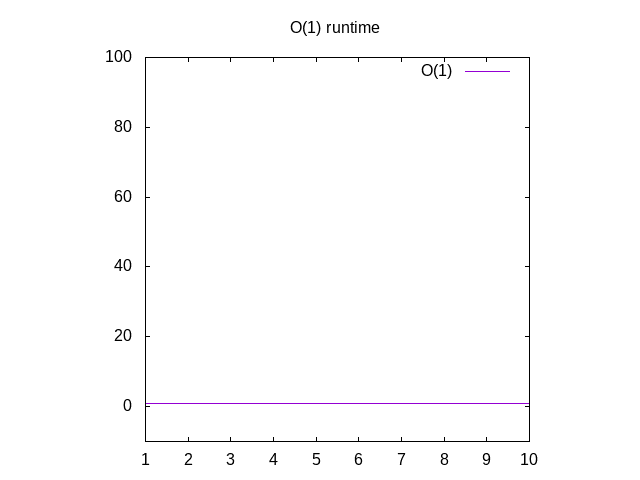
Kuva 3: Runtime ominaisuudet O(1) – funktion
Harkitse tämän toiminnon:
Alla on vertailu jokainen näistä kaavioita, viittaus., Voit nähdä, että O(n^2) – toiminto ei saada hidas hyvin nopeasti jos jotain, joka toimii jatkuvasti ajan on paljon parempi. Tämä on erityisen hyödyllistä, kun kyse on tietorakenteista, jotka postaan noin pian.
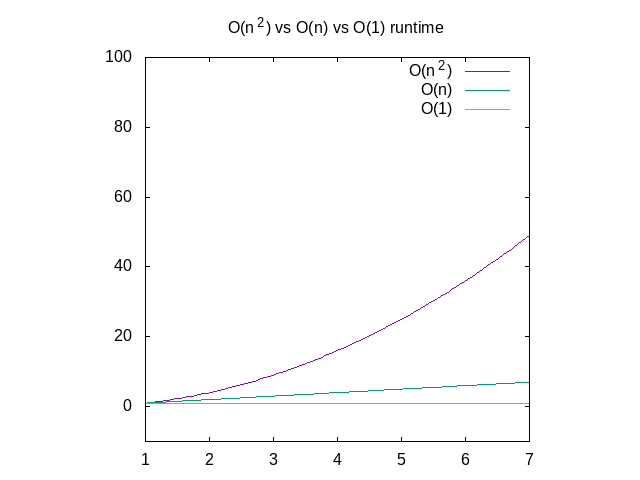
Kuva 4: Vertailu O(n2) vs. O(n) vs. O(1) – toiminnot
Tämä on melko korkean tason yleiskuvan Iso-O-notaatio, mutta hopefullygets olet perehtynyt aiheeseen., On coursera kurssi, joka voi antaa sinulle syvällisemmän näkymän tähän aiheeseen, mutta varoitetaan, että thatit hyppää mathematic notation hyvin nopeasti. Jos tässä ei ole mitään järkeä, lähetä sähköpostia.
Päivitys: olen myös kirjoittanut siitä, miten laskea Iso-O.
– olen ajatellut kirjoittaa kirjan tästä aiheesta. Jos tämä on haluaisitko nähdä, ilmaise kiinnostuksesi täällä.