Me klassisesti ajatella valoa kuten aina matkustaa suoria viivoja, mutta kun valonsäteet kulkevat lähellä este, niillä on taipumus taipua noin, että esteen ja tulee levittää. Diffraktio valon tapahtuu, kun valo aalto kulkee nurkkaan tai kautta aukko tai rako, joka on fyysisesti likimääräinen koko, tai jopa pienempi kuin valon aallonpituus.,

hyvin yksinkertainen osoitus diffraktio voidaan suorittaa pitämällä kättä edessä valonlähteen ja hitaasti sulkemalla kaksi sormea, kun tarkkailemalla valo välity niiden välillä. Kun sormet lähestyvät toisiaan ja tulevat hyvin lähelle toisiaan, alkaa nähdä sormien kanssa yhdensuuntaisia tummia viivoja. Yhdensuuntaiset viivat ovat todellisuudessa diffraktiokuvioita. Tämä ilmiö voi ilmetä myös, kun valo on ”taivutettu” noin hiukkasia, jotka ovat samaa suuruusluokkaa kuin valon aallonpituus., Hyvä esimerkki tästä on diffraktio auringonvalo pilvien, että me usein viitataan kuin hopeareunus on havainnollistettu Kuvassa 1, jossa on kaunis auringonlasku yli valtameren.
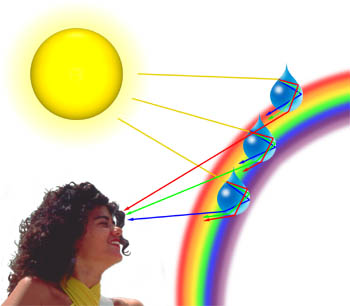
– Voimme usein tarkkailla pastelli sinisiä sävyjä, vaaleanpunainen, violetti ja vihreä pilviä, jotka syntyvät, kun valo on taittuneen alkaen vesipisaroita pilvet. Määrä diffraktio riippuu valon aallonpituus, lyhyemmillä aallonpituuksilla on taittuneen suuremmassa kulmassa kuin enää niitä (itse asiassa, sininen ja violetti valo ovat taittuneen suurempi kulma kuin on punainen valo)., Koska valo aalto kautta kulkeviin tunnelma kohtaamisia pisara vettä, kuten kuvassa alla, se on ensimmäinen taittuu veden ja ilman rajapintaan, se heijastuu se taas kohtaa käyttöliittymä. Vesipisaran sisällä edelleen kulkeva palkki taittuu jälleen, kun se iskee rajapintaan kolmannen kerran. Tämä viimeinen vuorovaikutus rajapinnan kanssa taittaa valon takaisin ilmakehään, mutta se myös hajottaa osan valosta alla kuvatulla tavalla., Tämä diffraktio elementti johtaa ilmiö tunnetaan Cellini on halo (tunnetaan myös nimellä Heiligenschein vaikutus), jossa kirkas rengas valo ympäröi varjo tarkkailijan pää.
ehdot diffraktio ja sironta käytetään usein synonyymeinä ja niitä pidetään lähes toistensa synonyymejä. Diffraktio kuvataan erikoistunut tapauksessa valon sironta, jossa esine säännöllisesti toistuva ominaisuuksia (kuten hila) tuottaa hallittu diffraktio valon diffraktio kuvio., Todellisessa maailmassa useimmat esineet ovat hyvin monimutkainen muoto ja se olisi pidettävä koostuu monista yksittäisistä diffraktio ominaisuuksia, jotka voivat yhdessä tuottaa satunnainen hajonta valoa.
Yksi klassinen ja keskeisimpiä käsitteitä, joihin diffraktio on yhden raon diffraktio optiset kokeilla, ensin tehdään alussa yhdeksästoista vuosisata. Kun valo aalto etenee viilto (tai aukko) tulos riippuu fyysinen koko aukon suhteen aallonpituus säteen., Tämä on havainnollistettu Kuvassa 3 olettaen yhtenäinen, yksivärisen aalto pääsee kohta lähde S, samanlainen valo, joka olisi valmistettu laser, joka kulkee aukon d ja on taittuneen, ensisijaisena valon säde lasku pisteen P ja ensimmäinen toissijainen maxima tapahtuu pisteessä Q.
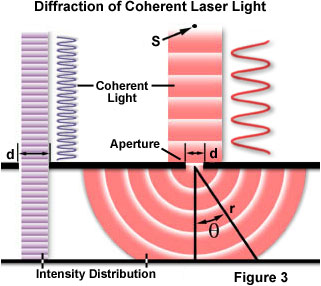
Kuten on esitetty vasemmalla puolella luku, kun aallonpituus (λ) on paljon pienempi kuin aukon leveys (d), aalto yksinkertaisesti kulkee eteenpäin suorassa linjassa, aivan kuten se olisi, jos se olisi hiukkasen tai ei aukon olivat läsnä., Kuitenkin, kun aallonpituus ylittää koko aukon, meidän kokemus diffraktio valon mukaan yhtälö:
Missä θ on kulma tapaus keski-eteneminen suuntaan ja ensimmäinen vähintään diffraktio kuvio. Kokeilu tuottaa kirkkaan keski enimmäismäärä, jota reunustaa molemmin puolin toissijainen maxima, intensiteetti kunkin menestyminen toissijainen suurin vähenee kun etäisyys keskustasta kasvaa. Kuva 4 havainnollistaa tätä kohtaa palkin voimakkuuden ja diffraktionsäteen havaintoalueella., Huomaa, että toissijaisten maksimien välillä esiintyvät minimit sijaitsevat π: n kerrannaisina.
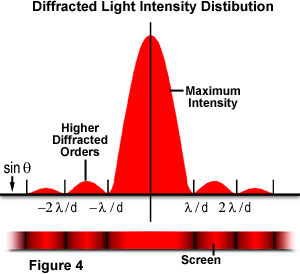
Tämä koe oli ensimmäinen selittää Augustin Fresnel, jotka yhdessä Thomas Young, tuottanut merkittäviä todisteita, jotka vahvistavat, että valo kulkee aaltoina. Luvuista yllä, näemme, miten johdonmukaista, monokromaattista valoa (tässä esimerkissä laser valaistus) pääsee pisteestä L on taittuneen, jonka aukon d., Fresnel olettaa, että amplitudi ensimmäisen kertaluvun maxima pisteessä Q (määritelty eQ) olisi yhtälöstä:
missä A on amplitudi tapaus aalto, r on etäisyys d ja K, ja f(x) on funktio χ, kaltevuus seikka käyttöön Fresnel.
Diffraktio Valon
Tutkia, miten valonsäde on taipuneen, kun se kulkee kapean raon tai aukon. Säädä aallonpituus ja aukon koko ja tarkkaile, miten tämä vaikuttaa diffraktiovoimakuvioon.,
Diffraktio valon pelaa ensiarvoisen rooli rajoittaa erotuskyky tahansa optinen laite (esimerkiksi: kamerat, kiikarit, kaukoputket, mikroskoopit, ja silmä). Ratkaisuvoima on optisen instrumentin kyky tuottaa erillisiä kuvia kahdesta vierekkäisestä pisteestä. Tämä on usein määräytyvät laatu linssit ja peilit väline sekä ominaisuuksia ympäröivän väliaineen (yleensä ilman). Valon aaltomainen luonne pakottaa lopullisen rajan kaikkien optisten instrumenttien ratkaisuvoimalle.,
– Meidän keskustelut diffraktio on käytetty viilto, kuten aukko, jonka läpi valo on taittuneen. Kaikissa optisissa instrumenteissa on kuitenkin pyöreät aukot, esimerkiksi silmän pupilli tai mikroskoopin Pyöreä kalvo ja linssit. Pyöreä aukot tuottaa diffraktio kuvioita samanlaisia kuin edellä on kuvattu, paitsi kuvio luonnollisesti näyttelyitä pyöreä symmetria. Matemaattinen analyysi diffraktio kuvioita valmistettu pyöreä aukko on kuvattu seuraavalla kaavalla:
missä θ(1) on kulma-asentoon ensimmäisen kertaluvun diffraktio minimit (ensimmäinen tumma rengas), λ on aallonpituus valon, d on halkaisija aukko, ja 1.22 on vakio. Useimmissa olosuhteissa, kulma θ(1) on hyvin pieni, joten lähentämisestä, että sin ja tan kulma ovat lähes yhtä suuret tuotot:
nämä yhtälöt käy ilmi, että keski-maksimi on suoraan verrannollinen λ/d, joten tämä maksimi enemmän levittää enää aallonpituuksilla ja pienemmät aukot., Toissijainen mimina diffraktio asettaa rajan hyödyllisiä suurennus objektiivit optinen mikroskopia, koska luontainen diffraktio valon linssit. Riippumatta siitä, kuinka täydellinen linssi voi olla, linssin tuottaman valonlähteen kuvaan liittyy toissijainen ja korkeampi kertaluku maxima. Tämä voitiin poistaa vain, jos objektiivin halkaisija oli ääretön. Kahta kohdetta, joiden etäisyys on pienempi kuin θ(1), ei voida ratkaista riippumatta siitä, kuinka suuri suurennusteho on., Kun nämä yhtälöt on johdettu kuvan kohta lähde kevyt ääretön etäisyys aukon, se on järkevä lähentämisestä erotuskyky mikroskoopilla, kun d on korvata halkaisija objektiivin.
Näin ollen, jos kahden objektit sijaitsevat etäisyydellä D toisistaan ja ovat etäisyydellä L tarkkailija, kulma (ilmaistu radiaaneina) välillä on:
joka johtaa meidät voi tiivistyä kaksi viimeistä yhtälöt saadaan:
Missä D(0) on pienin etäisyyden esineitä, joiden avulla ne voidaan ratkaista. Käyttämällä tätä yhtälöä, ihmisen silmä voi ratkaista esineitä erotettu etäisyys 0,056 millimetriä, kuitenkin photoreceptors verkkokalvon eivät ole aivan riittävän lähellä toisiaan, jotta tämä aste päätöslauselman, ja 0,1 millimetriä on realistisempi määrä normaaleissa olosuhteissa.
erotuskyky optiset mikroskoopit määräytyy useista tekijöistä, kuten mainittu, mutta kaikkein ihanteellinen olosuhteissa, tämä määrä on noin 0,2 mikrometriä., Tämä määrä on otettava huomioon optinen tasaus mikroskoopin, laatu linssit, sekä hallitseva valon aallonpituuksilla käytetään kuvan yksilö. Vaikka se on usein ei ole tarpeen laskea tarkka erotuskyky kunkin tavoitteen (ja olisi ajanhukkaa useimmissa tapauksissa), on tärkeää ymmärtää ominaisuudet mikroskoopin linssit, kuten niitä sovelletaan todelliseen maailmaan.
Edistää Kirjailijoiden
Mortimer Abramowitz – Olympus America, Inc., Kaksi Yrityskeskusta., Melville, New York, 11747.
Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.