osaamistavoitteet
- Tunnistaa pesäkkeitä, vertices, akselit, ja keskellä ellipsi.
- Kirjoita yhtälöt ellipsejä keskitetty alkuperä.
- Kirjoita yhtälöt ellipsejä ei keskitetty alkuperä.
kartioleikkauksen, tai conic, on muoto, jolloin risteävää oikea pyöreä kartio kone. Kulma, jossa taso leikkaa kartio määrittää muodon.,
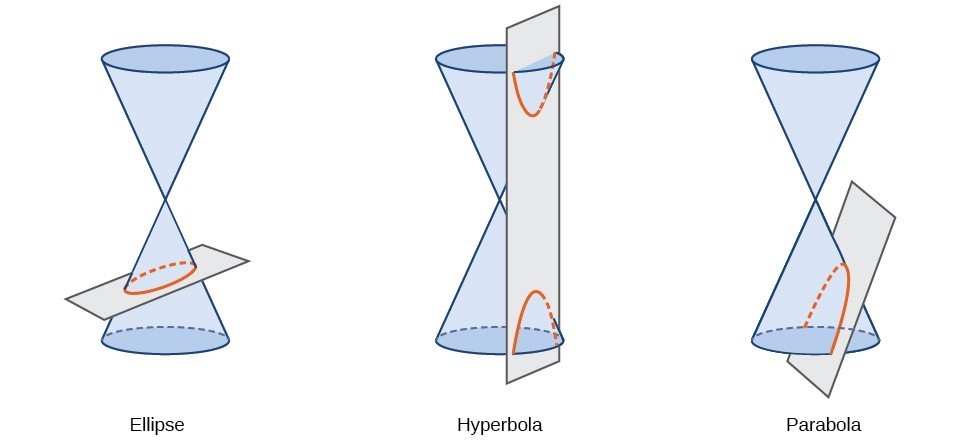
– Conic pääluokat voidaan kuvata myös joukko pistettä koordinaattitasoon. Myöhemmin tässä luvussa näemme, että kaavio tahansa quadratic yhtälö kaksi muuttujaa on conic osa. Yhtälöiden merkit ja muuttujan termien kertoimet määrittävät muodon. Tässä jaksossa keskitytään ellipsin yhtälön vakiomuodon neljään variaatioon. Ellipsi on kaikkien pisteiden joukko \left(x,y\right) tasossa siten, että niiden etäisyyksien summa kahdesta kiinteästä pisteestä on vakio., Jokaista kiinteää pistettä kutsutaan ellipsin tarkennukseksi (monikko: foci).
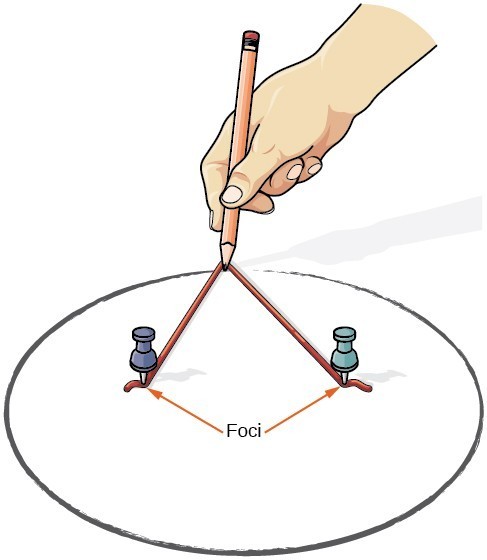
voimme piirtää ellipsin pahvinpalalla, kahdella peukalolla, lyijykynällä ja narulla. Aseta peukalot pahviin ellipsin pesäkkeiden muodostamiseksi. Leikkaa pala merkkijono on pitempi kuin etäisyys kahden nastoja (pituus merkkijono edustaa vakiona määritelmä). Kiinnitä narun jokainen pää kartonkiin ja jäljitä käyrä kynällä, joka on tarttunut narua vasten. Tuloksena on ellipsi.
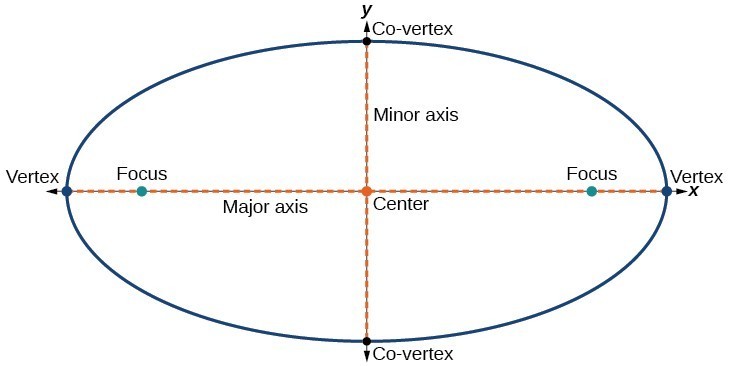
Jokainen ellipsi on kaksi symmetria-akselia., Pidempää akselia kutsutaan pääakseliksi ja lyhyempää akselia pienakseliksi. Pääakselin jokainen päätepiste on ellipsin huippupiste (monikko: vertices), ja molliakselin jokainen päätepiste on ellipsin co-vertex. Ellipsin keskipiste on sekä pää-että molliakselien keskipiste. Akselit ovat kohtisuorassa keskellä. Pesäkkeitä aina olla pääakseli, ja summa etäisyydet pesäkkeitä missään vaiheessa ellipsi (vakio summa) on suurempi kuin etäisyys pesäkkeitä.,
tässä osiossa rajoittaa ellipsejä niille, jotka on sijoitettu pystysuoraan tai vaakasuoraan koordinoida kone. Eli akselit joko makaavat x– ja y-akselien päällä tai ovat samansuuntaisia. Myöhemmin luvussa nähdään ellipsejä, joita pyöritetään koordinaatistossa.
työskennellä vaaka-ja pystysuunnassa ellipsejä koordinoida kone, pidämme kaksi tapausta: ne, jotka ovat keskitetty alkuperä ja ne, jotka ovat keskitetty samaan pisteeseen muut kuin alkuperä., Ensin opimme saamaan yhtälöt ellipsejä, ja sitten opimme kirjoittamaan yhtälöt ellipsejä vakiomuodossa. Myöhemmin käytämme oppimaamme piirtääksemme kaaviot.,v>Jos (x,y) on pisteen ellipsin, niin voimme määritellä seuraavat muuttujat:
\begin{align}d_1&=\text{etäisyyden } (-c,0) \text{ to } (x,y) \\ d_2&= \text{etäisyyden } (c,0) \text{ to } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
varten ellipsin keskipisteessä, alkuperä sen pääakselin X-akselilla ja
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1,
varten ellipsin keskipisteessä, alkuperä sen pääakselin Y-akselilla.,
Kirjoittaminen Yhtälöiden Ellipsejä Ole Keskitetty Alkuperä
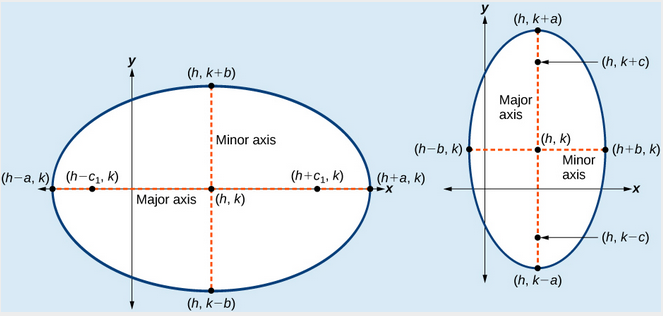
(a) Vaaka-ellipsi center \left(s,k\oikealla) (b) Pystysuuntainen ellipsi center \left(s,k\right)
Ratkaista Ongelmia, Joihin Sovelletaan Ellipsejä
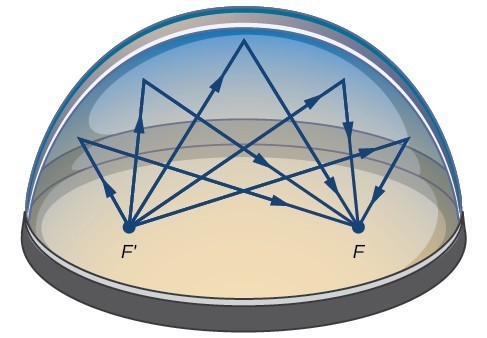
Monet reaalimaailman tilanteita voi edustaa ellipsejä, mukaan lukien kiertoradat planeettoja, satelliitit, kuita ja komeettoja, ja muotoja veneen köliä, peräsimet, ja joitakin lentokoneen siipiä. Litotripteriksi kutsuttu lääketieteellinen laite käyttää elliptisiä heijastimia hajottaakseen munuaiskiviä synnyttämällä ääniaaltoja., Joitakin rakennuksia, nimeltään kuiskaten chambers, on suunniteltu elliptinen kupolit niin, että henkilö kuiskaten yksi painopiste voi helposti kuulla, että joku seisoo muiden keskittyä. Tämä johtuu ellipsin akustisista ominaisuuksista. Kun ääniaalto on peräisin yksi painopiste kuiskaten jaosto, ääniaalto heijastuu pois elliptinen kupoli ja takaisin muiden keskittyä. Kuiskaus jaosto Museossa Tiede-ja teollisuusministeriön Chicagossa, kaksi ihmistä seisoo pesäkkeitä—noin 43 metriä toisistaan—voitte kuulla toisianne kuiskaus.