resultados de aprendizaje
- Identificar los focos, vértices, ejes y Centro de una elipse.
- Escribe ecuaciones de elipses centradas en el origen.
- escribir ecuaciones de elipses no centradas en el origen.
una sección cónica, o cónica, es una forma resultante de la intersección de un cono circular derecho con un plano. El ángulo en el que el plano se cruza con el cono determina la forma.,
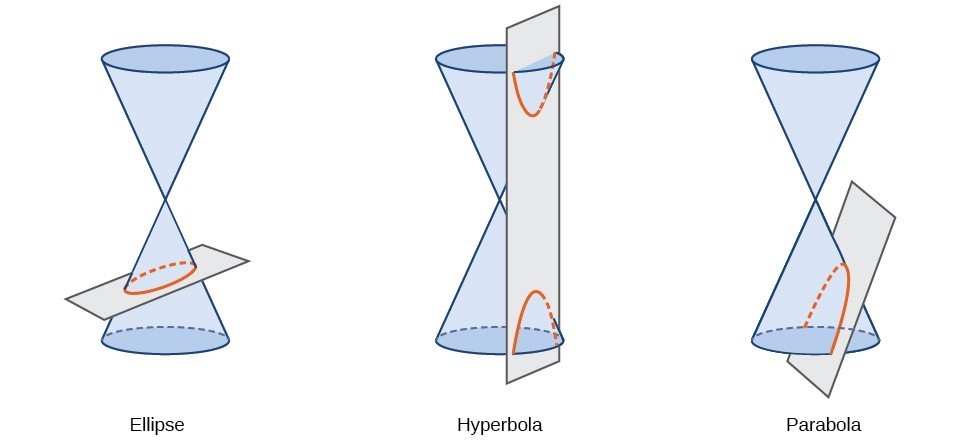
las secciones cónicas también se pueden describir mediante un conjunto de puntos en el plano de coordenadas. Más adelante en este capítulo veremos que el gráfico de cualquier ecuación cuadrática en dos variables es una sección cónica. Los signos de las ecuaciones y los coeficientes de los términos variables determinan la forma. Esta sección se centra en las cuatro variaciones de la forma estándar de la ecuación para la elipse. Una elipse es el conjunto de todos los puntos \left (x, y \ right) en un plano tal que la suma de sus distancias desde dos puntos fijos es una constante., Cada punto fijo se llama un foco (plural: focos) de la elipse.
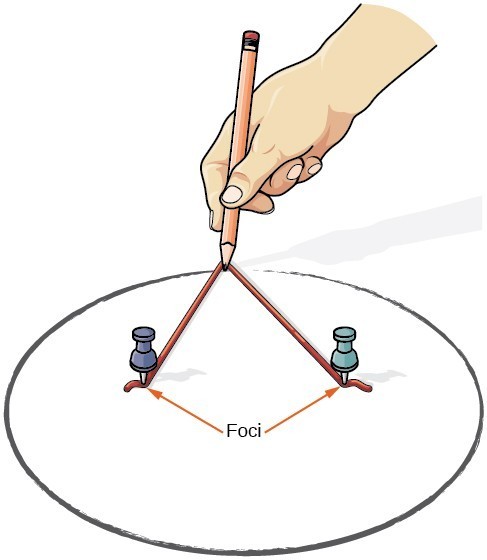
podemos dibujar una elipse usando un pedazo de cartón, dos chinchetas, un lápiz y una cuerda. Coloque las chinchetas en el cartón para formar los focos de la elipse. Corta un trozo de cuerda más largo que la distancia entre las dos chinchetas (la longitud de la cuerda representa la constante en la definición). Pega cada extremo de la cuerda al cartón y traza una curva con un lápiz tenso contra la cuerda. El resultado es una elipse.
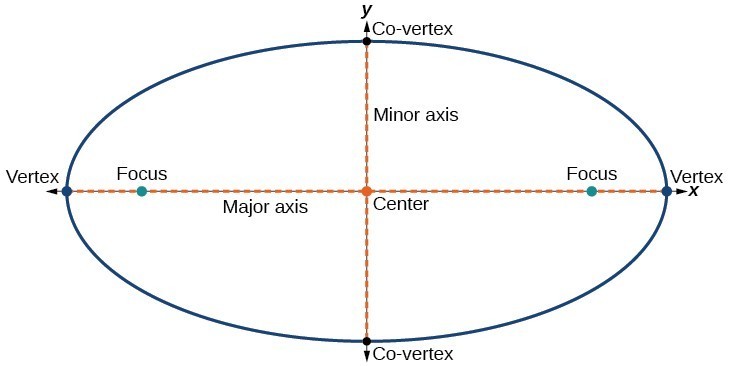
Cada elipse tiene dos ejes de simetría., El eje más largo se llama eje mayor, y el eje más corto se llama eje menor. Cada extremo del eje mayor es el vértice de la elipse (plural: vértices), y cada extremo del eje menor es un co-vértice de la elipse. El Centro de una elipse es el punto medio de los ejes mayor y menor. Los ejes son perpendiculares en el centro. Los focos siempre se encuentran en el eje mayor, y la suma de las distancias desde los focos a cualquier punto de la elipse (la suma constante) es mayor que la distancia entre los focos.,
en esta sección restringimos las elipses a aquellas que están posicionadas vertical u horizontalmente en el plano de coordenadas. Es decir, los ejes se encuentran o son paralelos a los ejes x e Y. Más adelante en el capítulo, veremos elipses que se giran en el plano de coordenadas.
para trabajar con elipses horizontales y verticales en el plano de coordenadas, consideramos dos casos: los que están centrados en el origen y los que están centrados en un punto distinto al origen., Primero aprenderemos a derivar las ecuaciones de elipses, y luego aprenderemos a escribir las ecuaciones de elipses en forma estándar. Más adelante usaremos lo que aprendamos para dibujar los gráficos.,v>Si (x,y) es un punto de la elipse, entonces podemos definir las siguientes variables:
\begin{align}d_1&=\text{la distancia de } (-c,0) \text{ a } (x,y) \\ d_2&= \text{la distancia de } (c,0) \text{ a } (x,y) \end{alinean}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
para una elipse centrada en el origen con su eje mayor en el eje X y
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
para una elipse centrada en el origen con su eje mayor en el eje.,
escribir ecuaciones de elipses No centradas en el origen
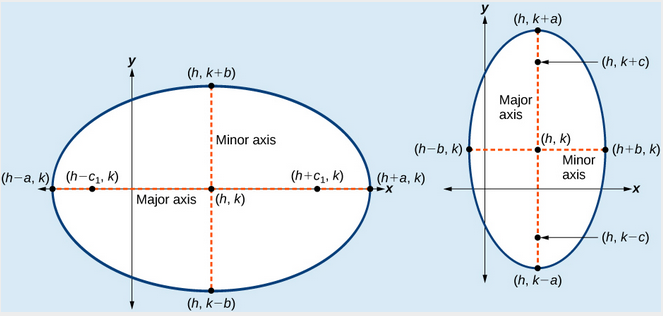
(a) elipse Horizontal con el centro \left(h,k\right) (b) elipse Vertical con el centro \left(h,k\right)
resolver problemas aplicados/h2>
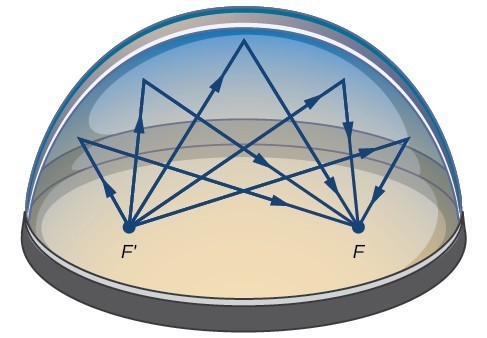
muchas situaciones del mundo real pueden ser representadas por elipses, incluyendo órbitas de planetas, satélites, lunas y cometas, y formas de quillas de barcos, timones y algunas alas de aviones. Un dispositivo médico llamado litotriptor utiliza reflectores elípticos para romper los cálculos renales mediante la generación de ondas sonoras., Algunos edificios, llamados cámaras susurrantes, están diseñados con cúpulas elípticas para que una persona que susurra en un foco pueda ser escuchada fácilmente por alguien de pie en el otro foco. Esto ocurre debido a las propiedades acústicas de una elipse. Cuando una onda de sonido se origina en un foco de una cámara susurrante, la onda de sonido se reflejará en la cúpula elíptica y volverá al otro foco. En la cámara de los susurros en el Museo de Ciencia e Industria de Chicago, dos personas de pie en los focos, a unos 43 pies de distancia, pueden escucharse susurrar.