Support Vector Machine o SVM es uno de los Algoritmos de aprendizaje supervisado más populares, que se utiliza para la clasificación, así como para problemas de regresión. Sin embargo, principalmente, se utiliza para problemas de clasificación en el aprendizaje automático.
el objetivo del algoritmo SVM es crear la mejor línea o límite de decisión que pueda segregar el espacio n-dimensional en clases para que podamos colocar fácilmente el nuevo punto de datos en la categoría correcta en el futuro., Este límite de mejor decisión se llama hiperplano.
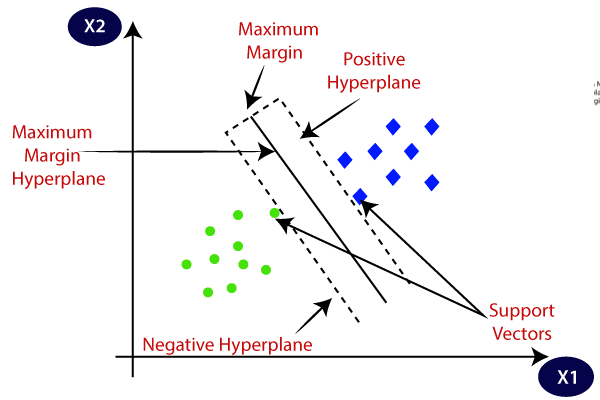
SVM elige los puntos extremos/vectores que ayudan a crear el hiperplano. Estos casos extremos se llaman como vectores de soporte, y por lo tanto el algoritmo se denomina como máquina vectorial de soporte. Considere el siguiente diagrama en el que hay dos categorías diferentes que se clasifican utilizando un límite de decisión o hiperplano:
Ejemplo: SVM se puede entender con el ejemplo que hemos utilizado en el clasificador KNN., Supongamos que vemos un gato extraño que también tiene algunas características de los perros, por lo que si queremos un modelo que pueda identificar con precisión si se trata de un gato o un perro, por lo que dicho modelo se puede crear mediante el uso del algoritmo SVM. Primero entrenaremos a nuestro modelo con muchas imágenes de gatos y perros para que pueda aprender sobre diferentes características de gatos y perros, y luego lo probaremos con esta extraña criatura. Así como vector de soporte crea un límite de decisión entre estos dos datos (gato y perro) y elegir casos extremos (vectores de soporte), verá el caso extremo de gato y perro., Sobre la base de los vectores de soporte, lo clasificará como un gato. Considere el siguiente diagrama:
el algoritmo SVM se puede usar para detección de rostros, clasificación de imágenes, categorización de texto, etc.
tipos de SVM
SVM puede ser de dos tipos:
- SVM lineal: el SVM lineal se usa para datos linealmente separables, lo que significa que si un conjunto de datos se puede clasificar en dos clases utilizando una sola línea recta, entonces dichos datos se denominan datos linealmente separables, y el clasificador se usa llamado clasificador SVM lineal.,
- SVM no lineal: el SVM no lineal se usa para datos separados no linealmente, lo que significa que si un conjunto de datos no se puede clasificar mediante el uso de una línea recta, entonces dichos datos se denominan datos no lineales y el clasificador utilizado se denomina clasificador SVM no lineal.
hiperplano y vectores de soporte en el algoritmo SVM:
hiperplano: puede haber múltiples líneas / límites de decisión para segregar las clases en el espacio n-dimensional, pero necesitamos encontrar el mejor límite de decisión que ayude a clasificar los puntos de datos. Este mejor límite se conoce como el hiperplano de SVM.,
Las dimensiones del hiperplano dependen de las entidades presentes en el conjunto de datos, lo que significa que si hay 2 entidades (como se muestra en la imagen), el hiperplano será una línea recta. Y si hay 3 características, entonces hyperplane será un plano de 2 dimensiones.
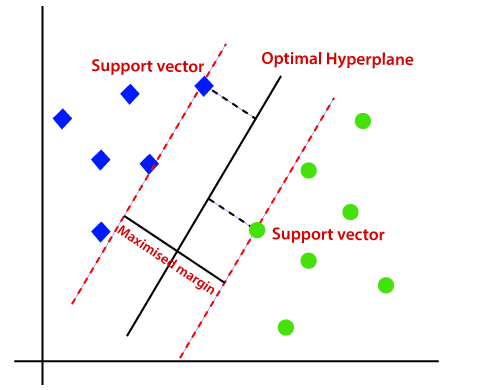
siempre creamos un hiperplano que tiene un margen máximo, lo que significa la distancia máxima entre los puntos de datos.
vectores de soporte:
los puntos de datos o vectores que son los más cercanos al hiperplano y que afectan la posición del hiperplano se denominan como Vector de soporte., Dado que estos vectores soportan el hiperplano, por lo tanto llamado vector de soporte.
¿cómo funciona SVM?
SVM lineal:
el funcionamiento del algoritmo SVM se puede entender usando un ejemplo. Supongamos que tenemos un conjunto de datos que tiene dos etiquetas (verde y azul), y el conjunto de datos tiene dos características x1 y x2. Queremos un clasificador que pueda clasificar el par (x1, x2) de coordenadas en verde o azul. Considere la siguiente imagen:
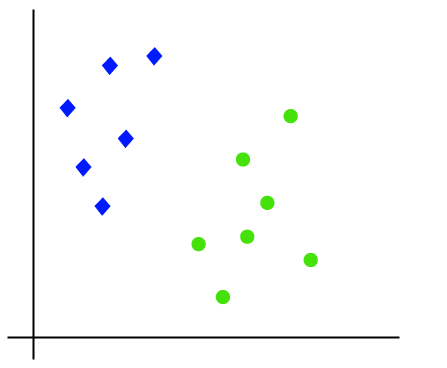
así que como es un espacio 2D, simplemente usando una línea recta, podemos separar fácilmente estas dos clases., Pero puede haber varias líneas que pueden separar estas clases. Considere la siguiente imagen:
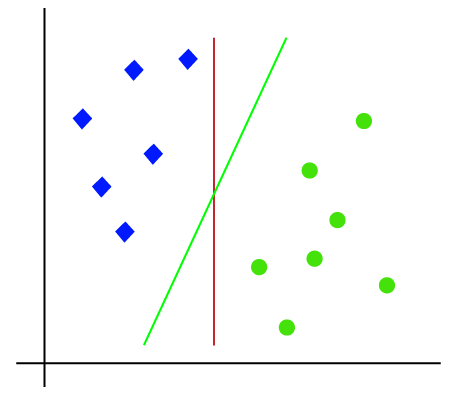
por lo tanto, el algoritmo SVM ayuda a encontrar la mejor línea o límite de decisión; este mejor límite o región se llama como un hiperplano. El algoritmo SVM encuentra el punto más cercano de las líneas de ambas clases. Estos puntos se llaman vectores de soporte. La distancia entre los vectores y el hiperplano se llama margen. Y el objetivo de SVM es maximizar este margen. El hiperplano con margen máximo se denomina hiperplano óptimo.,
SVM no lineal:
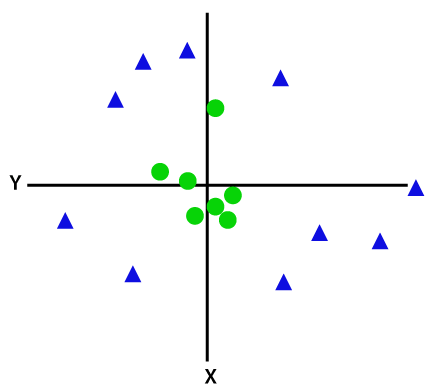
si los datos están dispuestos linealmente, entonces podemos separarlos usando una línea recta, pero para datos no lineales, no podemos dibujar una sola línea recta. Considere la siguiente imagen:
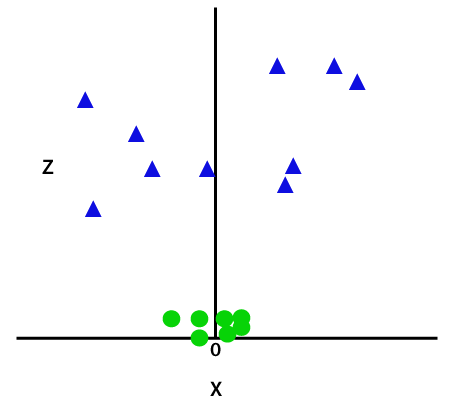
así que para separar estos puntos de datos, necesitamos agregar una dimensión más. Para datos lineales, hemos utilizado dos dimensiones x E y, por lo que para datos no lineales, agregaremos una tercera dimensión z., Se puede calcular como:
z=x2 +y2
al agregar la tercera dimensión, el espacio de muestra se convertirá en la siguiente imagen:
así que ahora, SVM dividirá los conjuntos de datos en clases de la siguiente manera. Considere la siguiente imagen:
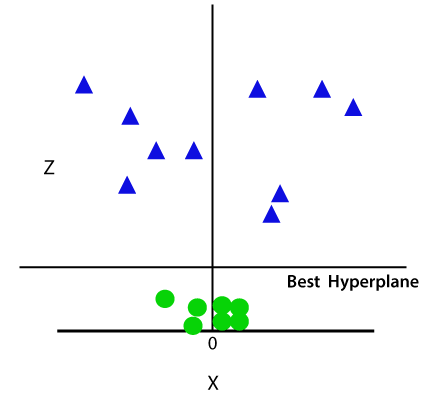
ya que estamos en el espacio 3D, por lo tanto, se ve como un plano paralelo al eje X. Si lo convertimos en espacio 2d con z=1, entonces se convertirá en:
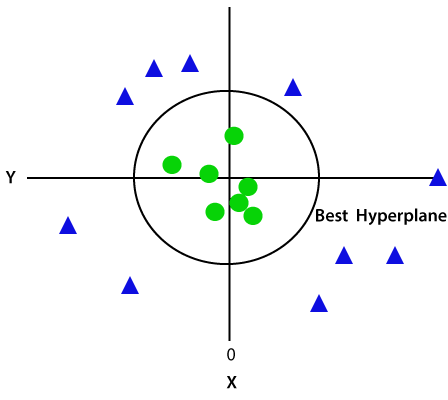
por lo tanto, obtenemos una circunferencia de radio 1 en el caso de datos no lineales.,
Python implementación de Support Vector Machine
ahora implementaremos el algoritmo SVM usando Python. Aquí usaremos el mismo dataset user_data, que hemos utilizado en regresión logística y clasificación KNN.
- Paso de Pre-procesamiento de datos
hasta el paso de pre-procesamiento de datos, el código seguirá siendo el mismo. A continuación se muestra el código:
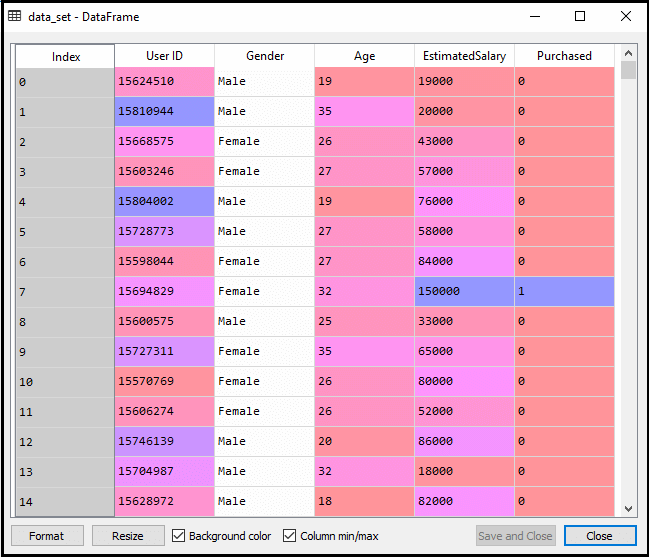
después de ejecutar el código anterior, procesaremos previamente los datos., El código dará el conjunto de datos como:
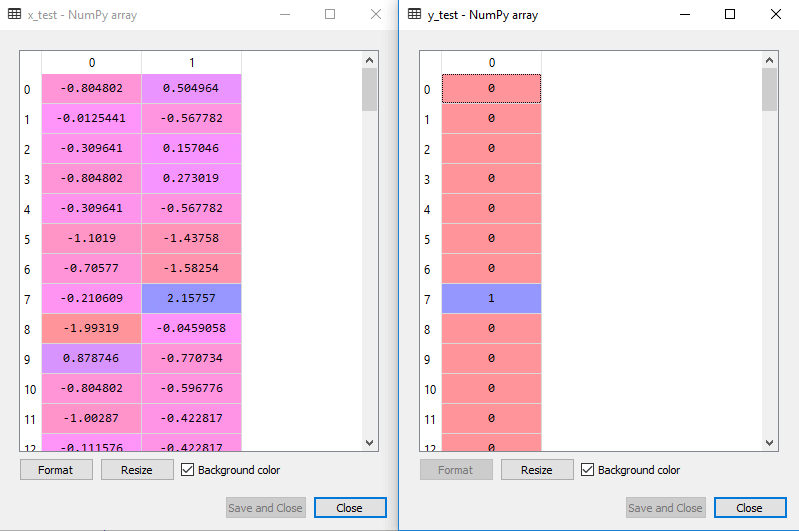
La escala de salida para el conjunto de pruebas será:
Ajuste el clasificador SVM para el conjunto de entrenamiento:
Ahora el conjunto de entrenamiento va a ser instalado en el clasificador SVM. Para crear el clasificador SVM, importaremos la clase SVC desde Sklearn.biblioteca svm. A continuación se muestra el código para ello:
en el código anterior, hemos utilizado kernel=’linear’, ya que aquí estamos creando SVM para datos linealmente separables. Sin embargo, podemos cambiarlo por datos no lineales., Y luego ajustamos el clasificador al conjunto de datos de entrenamiento (x_train, y_train)
salida:
el rendimiento del modelo se puede alterar cambiando el valor de C(Factor de regularización), gamma y kernel.
- predecir el resultado del conjunto de pruebas:
Ahora, vamos a predecir la salida para el conjunto de pruebas. Para esto, vamos a crear un nuevo vector y_pred. A continuación se muestra el código para ello:
después de obtener el vector y_pred, podemos comparar el resultado de y_pred y y_test para verificar la diferencia entre el valor real y el valor predicho.,
salida: a continuación se muestra la salida para la predicción del conjunto de pruebas:

- creando la matriz de confusión:
ahora veremos el rendimiento del clasificador SVM que cuántas predicciones incorrectas hay en comparación con el clasificador de regresión logística. Para crear la matriz de confusión, necesitamos importar la función confusion_matrix de la biblioteca sklearn. Después de importar la función, la llamaremos usando una nueva variable cm. La función toma dos parámetros, principalmente y_true (los valores reales) y y_pred (el valor de destino devuelto por el clasificador)., A continuación se muestra el código para ello:
salida:
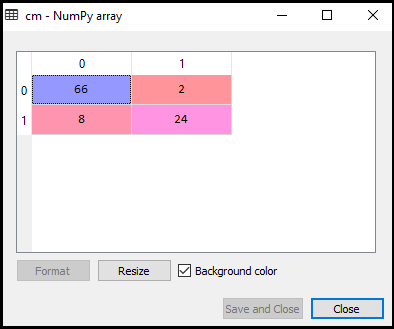
Como podemos ver en la imagen de salida anterior, hay 66+24= 90 predicciones correctas y 8+2= 10 predicciones correctas. Por lo tanto, podemos decir que nuestro modelo SVM mejoró en comparación con el modelo de regresión logística.,
- visualizando el resultado del conjunto de entrenamiento:
ahora visualizaremos el resultado del conjunto de entrenamiento, a continuación se muestra el código para él:
salida:
ejecutando el código anterior, obtendremos la salida como:
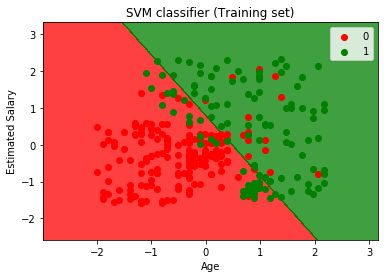
Como podemos ver, la salida anterior aparece similar a la salida de regresión logística. En la salida, tenemos la línea recta como hiperplano porque hemos utilizado un núcleo lineal en el clasificador. Y también hemos discutido anteriormente que para el espacio 2d, el hiperplano en SVM es una línea recta.,
- visualizando el resultado del conjunto de pruebas:
salida:
ejecutando el código anterior, obtendremos la salida como:
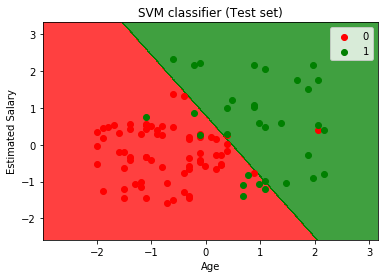
Como podemos ver en la imagen de salida anterior, el clasificador SVM ha dividido a los usuarios en dos regiones (compradas o no compradas). Los usuarios que compraron el SUV están en la región roja con los puntos de dispersión rojos. Y los usuarios que no compraron el SUV están en la región verde con puntos de dispersión verdes. El hiperplano ha dividido las dos clases en Variable comprada y no comprada.