Asunción de normalidad de la variable dependiente
la prueba t independiente requiere que la variable dependiente se distribuya aproximadamente normalmente dentro de cada grupo.
Nota: técnicamente, son los residuos los que deben distribuirse normalmente, pero para una prueba t independiente, ambos le darán el mismo resultado.,
puede probar esto usando una serie de pruebas diferentes, pero la prueba de normalidad de Shapiro-Wilks o un método gráfico, como un gráfico Q-Q, son muy comunes. Puede ejecutar estas pruebas utilizando las estadísticas de SPSS, cuyo procedimiento se puede encontrar en nuestra Guía de pruebas de normalidad. Sin embargo, la prueba t se describe como una prueba robusta con respecto a la asunción de normalidad. Esto significa que alguna desviación de la normalidad no tiene una gran influencia en las tasas de error de tipo I. La excepción a esto es si la relación entre el tamaño de grupo más pequeño y más grande es mayor que 1.,5 (el más grande comparado con el más pequeño).
qué hacer cuando viola la suposición de normalidad
Si encuentra que uno o ambos datos de su grupo no están distribuidos aproximadamente normalmente y los tamaños de los grupos difieren mucho, tiene dos opciones: (1) transformar sus datos para que los datos se distribuyan normalmente (para hacer esto en Estadísticas SPSS, consulte nuestra guía sobre Transformación de datos), o (2) ejecutar la prueba U de Mann-Whitney, que es una prueba no paramétrica que no requiere la suposición de normalidad (para ejecutar esta prueba en estadísticas SPSS, consulte nuestra guía en la prueba U de Mann-Whitney).,
suposición de homogeneidad de varianza
la prueba t independiente asume que las varianzas de los dos grupos que está midiendo son iguales en la población. Si sus varianzas son desiguales, esto puede afectar la tasa de error de tipo I. El supuesto de homogeneidad de varianza puede ser probado usando la prueba de igualdad de varianzas de Levene, que se produce en las estadísticas SPSS cuando se ejecuta el procedimiento de prueba t independiente., Si ha ejecutado la prueba de igualdad de varianzas de Levene en las estadísticas SPSS, obtendrá un resultado similar al siguiente:

Esta prueba de homogeneidad de varianza proporciona una estadística F y un valor de significación (valor p). Nos preocupa principalmente el valor de significancia-si es mayor que 0.05 (es decir, p > .05), nuestras varianzas de grupo pueden ser tratadas como iguales. Sin embargo, si p < 0.05, tenemos varianzas desiguales y hemos violado el supuesto de homogeneidad de las varianzas.,
superar una violación del supuesto de homogeneidad de varianza
si la prueba de Levene para la igualdad de varianzas es estadísticamente significativa, lo que indica que las varianzas de grupo son desiguales en la población, se puede corregir esta violación No utilizando la estimación agrupada para el término de error para el estadístico t, sino utilizando un ajuste a los grados de libertad utilizando el método de Welch-Satterthwaite., En realidad, probablemente nunca haya oído hablar de estos ajustes porque las estadísticas de SPSS ocultan esta información y simplemente etiquetan las dos opciones como» varianzas iguales asumidas «y» varianzas iguales no asumidas » sin indicar explícitamente las pruebas subyacentes utilizadas., Sin embargo, puede ver la evidencia de estas pruebas de la siguiente manera:
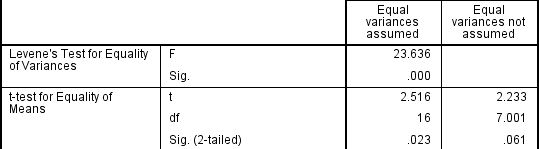
a partir del resultado de la prueba de Levene para la igualdad de varianzas, podemos rechazar la hipótesis nula de que no hay diferencia en las varianzas entre los grupos y aceptar la hipótesis alternativa de que hay una diferencia estadísticamente significativa en las varianzas entre los grupos., El efecto de no poder asumir varianzas iguales es evidente en la columna final de la figura anterior donde vemos una reducción en el valor del estadístico t y una gran reducción en los grados de libertad (df). Esto tiene el efecto de aumentar el valor de p Por encima del nivel de significancia crítica de 0,05. En este caso, por lo tanto, no aceptamos la hipótesis alternativa y aceptamos que no hay diferencias estadísticamente significativas entre medias. Esta no habría sido nuestra conclusión si no hubiéramos probado la homogeneidad de las variaciones.