Esta es la primera de una serie de tres publicaciones. El segundo post habla de cómo calcular Big-O. El tercer artículo habla de entender la definición formal de Big-O.
la notación Big-O solía ser un concepto realmente aterrador para mí. Pensé que así es como los programadores» reales » hablaban de su código. Fue todo más aterrador porque las descripciones académicas (como Wikipedia) me hicieron muy poco sentido. Esto es frustrante porque los conceptos subyacentes no son realmente tan difíciles.,
en pocas palabras, la notación Big-O es cómo los programadores hablan sobre los algoritmos. Los algoritmos son otro tema aterrador que cubriré en otro post, pero para nuestros propósitos, digamos que «algoritmo» significa función en su programa (que no está demasiado lejos). La gran Onotación de una función está determinada por cómo responde a diferentes entradas. ¿Qué tan lento es si le damos una lista de 1000 cosas para trabajar en lugar de una lista de 1 cosa?
Considere la posibilidad de este código:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Así que si llamamos a esta función como item_in_list(2, ), se debe bastante rápido., Hacemos un bucle sobre cada cosa en la lista y si encontramos el primer argumento de nuestra función, devolvemos True. Si llegamos al final y no lo encontramos, devuelve False.
La «complejidad» de esta función es O(n). Voy a explicar lo que esto significa en un segundo, pero vamos a desglosar esta síntesis matemática. O(n)se lee» orden de N»porque la función O también se conoce como la función de orden. Creo que esto es porque estamos haciendo una aproximación, que trata en «Órdenes de magnitud».,
«órdenes de magnitud» es otro término matemático que básicamente indica la diferencia entre clases de números. Piensa en la diferencia entre 10 y 100. Si te imaginas a 10 de tus amigos cercanos y a 100 personas, esa es una gran diferencia. Del mismo modo, la diferencia entre 1,000 y 10,000 es bastante grande (de hecho, es la diferencia entre un auto junker y uno ligeramente usado). Resulta que en aproximación, mientras estés dentro de un orden de magnitud,estás bastante cerca., Si adivinara el número de gumballs en amachine, estaría dentro de un orden de magnitud si dijera 200 gumballs. 10.000 gumballs estarían muy lejos.

Figura 1: Una máquina de gumball cuyo número de chicles es, probablemente, dentro de un orden de magnitud de 200.
volver a diseccionar O(n), esto dice que si tuviéramos que graficar el tiempo que tarda en ejecutar esta función con entradas de diferentes tamaños (por ejemplo, unarray de 1 Elemento, 2 elementos, 3 elementos, etc.), veríamos que corresponde aproximadamente al número de elementos en la matriz., Esto se llama un gráfico lineal. Esto significa que la línea es básicamente recta si usted fuera a graficarla.
algunos de ustedes pueden haber captado que si, en el ejemplo de código anterior, ouritem era siempre el primer elemento de la lista, nuestro código sería reallyfast! Esto es cierto, pero Big-O tiene que ver con el peor rendimiento aproximado de hacer algo. El peor caso para el código anterior es que lo que estamos buscando no está en la lista en absoluto. (Nota: el término matemático para esto es «límite superior», lo que significa que habla sobre el límite matemático de lo terrible).,
Si desea ver una gráfica de estas funciones, usted ignorar el O()función y cambio de la variable n para x. A continuación, puede escribir thatinto Wolfram Alpha como «plot x» que le mostrará una diagonalina. La razón por la que cambia n por x es que su programa gráfico quiere x como su nombre de variable porque corresponde al xaxis. El eje x cada vez más grande de izquierda a derecha corresponde togiving matrices más grandes y más grandes a su función., El eje y representa el tiempo, por lo que cuanto más alta es la línea, más lenta es.
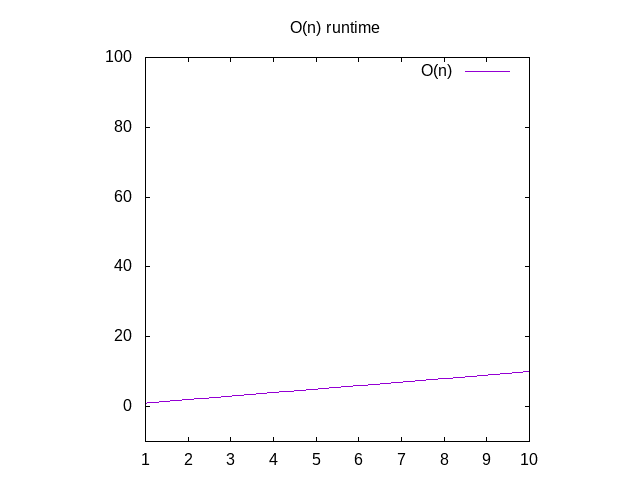
Figura 2: Características de tiempo de ejecución de una función o (n)
Considere esta función:
def is_none(item): return item is None
Esto es un poco de un ejemplo tonto, pero tengan paciencia conmigo. Esta función se llama O(1) que se llama «tiempo constante». Lo que esto significa es que no importa cuán grande sea nuestra entrada, siempre toma la misma cantidad de tiempo para calcular las cosas., Si vuelve a Wolfram y plot 1, verá que siempre permanece igual, sin importar cuán a la derecha vayamos. Si youpass en una lista de 1 millones de enteros, tomará aproximadamente el mismo tiempo como si fueras a pasar en una lista de 1 entero. El tiempo constante se considera el mejor escenario para una función.
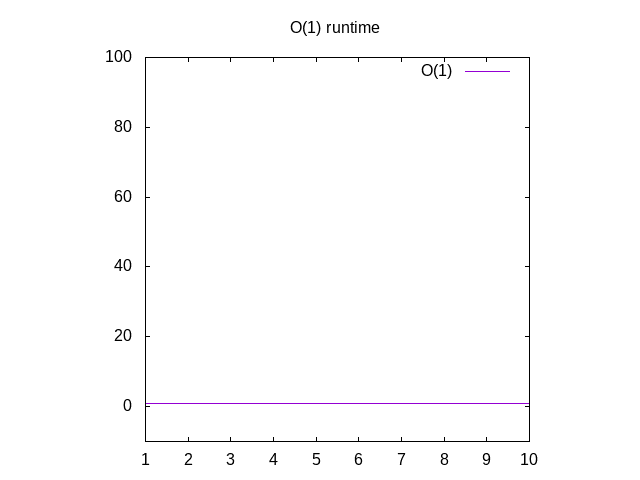
Figura 3: Características de tiempo de ejecución de una función O(1)
considere esta función:
a continuación se muestra una comparación de cada uno de estos gráficos, para referencia., Puede ver que una función O(n^2) se ralentizará muy rápidamente donde como algo que opera en tiempo constante será mucho mejor. Esto es particularmente útil cuando se trata de estructuras de datos, sobre las que publicaré pronto.
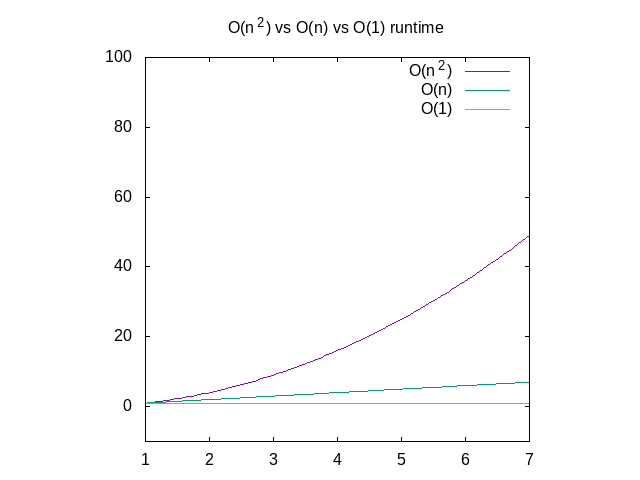
Figura 4: Comparación de funciones o(n2) vs O(n) vs O (1)
Esta es una descripción general de nivel bastante alto de la notación Big-O, pero con la esperanza de que se familiarice con el tema., Hay un curso de coursera que puede darle una visión más profunda de este tema, pero tenga en cuenta que saltará a la notación matemática muy rápidamente. Si algo aquí no tiene sentido, envíame un correo electrónico.
actualización: también he escrito sobre cómo calcular Big-O.
estoy pensando en escribir un libro sobre este tema. Si esto es algo que le gustaría ver, por favor exprese su interés aquí.