la Varianza mide la distancia de un conjunto de datos se dispersa. Una varianza de cero indica que todos los valores de los datos son idénticos. Todas las varianzas distintas de cero son positivas.

Una pequeña varianza indica que los puntos de datos tienden a ser muy cercanos a la media, y entre sí., Una varianza alta indica que los puntos de datos están muy separados de la media y entre sí. La varianza es el promedio de las distancias cuadradas de cada punto a la media.

el proceso de encontrar la varianza es muy similar a encontrar la desviación absoluta media MAD. la única diferencia es la cuadratura de las distancias.
Proceso: (1) Encontrar la media (promedio) del conjunto. (2) reste cada valor de datos de la media para encontrar su distancia de la media. (3) cuadrar todas las distancias. (4) suma todos los cuadrados de las distancias., (4) Dividir por el número de piezas de datos (para varianza de población).

un problema con la varianza es que no tiene la misma unidad de medida que los datos originales. Por ejemplo, los datos originales que contienen longitudes medidas en pies tienen una varianza medida en pies cuadrados.,

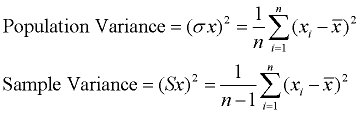Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Si se calcula a mano, siempre lleve más decimales dentro de los cálculos de lo que se espera para el resultado final. Si trabaja con una calculadora, lleve el valor completo de las entradas de la calculadora hasta que llegue al resultado final.

desviación Estándar de la muestra cuánto de la variación (dispersión, difusión, dispersión) de la media existe., Representa una desviación «típica» de la media. Es una medida popular de variabilidad porque regresa a las unidades de medida originales del conjunto de datos.

una desviación estándar baja indica que los puntos de datos tienden a estar muy cerca de la media. Una desviación estándar alta indica que los puntos de datos se distribuyen en un amplio rango de valores.
la desviación estándar puede considerarse como una forma «estándar» de saber qué es normal (típico), qué es muy grande y qué es muy pequeño en el conjunto de datos.,

la desviación estándar es una medida popular de variabilidad porque retorna a las unidades de medida originales del conjunto de datos. Por ejemplo, los datos originales que contienen longitudes medidas en pies tienen una desviación estándar también medida en pies.,

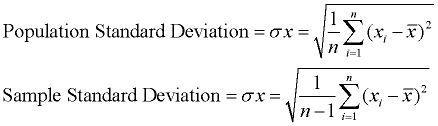Para calcular la desviación estándar con la mano:
La desviación estándar es simplemente la raíz cuadrada de la varianza.
esta descripción es para calcular la desviación estándar de la población. Si se necesita la desviación estándar de la muestra, divida por n – 1 en lugar de n., Dado que la desviación estándar es la raíz cuadrada de la varianza, primero debemos calcular la varianza.
1. Encuentra la media.
2. Reste la media de cada valor de datos y cuadrar cada una de estas diferencias (las diferencias cuadradas).
3. Encuentre el promedio de las diferencias cuadradas (sumarlas y dividirlas por el recuento de los valores de datos). Esta será la varianza.,

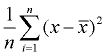la varianza
4. Toma la raíz cuadrada. Esta será la desviación estándar de la población. Redondee la respuesta de acuerdo con las direcciones en el problema.

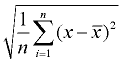desviación estándar

La Curva Normal

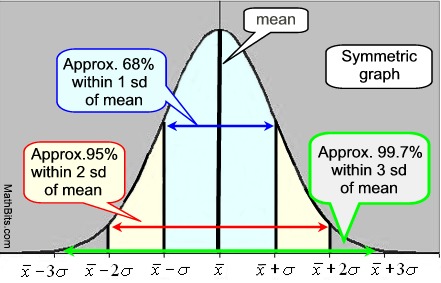
Una curva normal es simétrica, curva en forma de campana., El centro del gráfico es la media, y la altura y el ancho del gráfico están determinados por la desviación estándar. Cuando la desviación estándar es pequeña, la curva será alta y estrecha en propagación. Cuando la desviación estándar es grande, la curva será corta y amplia en propagación. La media y la mediana tienen el mismo valor en una curva normal.

la Curva Normal Regla Empírica:
Aproximadamente …

• el 68% de los datos se encuentran dentro de una desviación estándar de la media.,

• el 95% de los datos se encuentran dentro de dos desviaciones estándar de la media.

• el 99,7% de los datos se encuentran dentro de tres desviaciones estándar de la media.

IQR para una curva normal es 1.34896 x desviación estándar.