Introducción
la regresión lineal, también conocida como regresión lineal simple o regresión lineal bivariada, se utiliza cuando queremos predecir el valor de una variable dependiente en función del valor de una variable independiente. Por ejemplo, podría usar la regresión lineal para comprender si el rendimiento del examen se puede predecir en función del tiempo de revisión (p. ej.,, su variable dependiente sería «rendimiento del examen», medido de 0 a 100 puntos, y su variable independiente sería» tiempo de revisión», medido en horas). Alternativamente, podría usar la regresión lineal para comprender si el consumo de cigarrillos se puede predecir en función de la duración del tabaquismo (es decir, su variable dependiente sería «consumo de cigarrillos», medido en términos del número de cigarrillos consumidos diariamente, y su variable independiente sería «duración del tabaquismo», medida en días). Si tiene dos o más variables independientes, en lugar de solo una, debe usar regresión múltiple., Alternativamente, si solo desea establecer si existe una relación lineal, podría usar la correlación de Pearson.
Nota: La variable dependiente también se conoce como variable de resultado, objetivo o criterio, mientras que la variable independiente también se conoce como variable predictora, explicativa o regresora. En última instancia, sea cual sea el término que utilice, es mejor ser consistente. Nos referiremos a ellas como variables dependientes e independientes a lo largo de esta guía.,
en esta guía, le mostramos cómo realizar la regresión lineal utilizando Stata, así como interpretar y reportar los resultados de esta prueba. Sin embargo, antes de presentarle este procedimiento, debe comprender las diferentes suposiciones que deben cumplir sus datos para que la regresión lineal le brinde un resultado válido. Discutimos estas suposiciones a continuación.
stata
suposiciones
hay siete «suposiciones» que sustentan la regresión lineal. Si no se cumple cualquiera de estas siete suposiciones, no puede analizar sus datos utilizando linear porque no obtendrá un resultado válido., Dado que las suposiciones #1 y #2 se relacionan con su elección de variables, no se pueden probar para usar Stata. Sin embargo, usted debe decidir si su estudio cumple con estos supuestos antes de seguir adelante.
- suposición # 1: su variable dependiente debe medirse en el nivel continuo., Ejemplos de tales variables continuas incluyen la altura (medida en pies y pulgadas), la temperatura (medida en oC), el salario (medido en dólares estadounidenses), el tiempo de revisión (medido en horas), la inteligencia (medida utilizando la puntuación de coeficiente intelectual), el tiempo de reacción (medido en milisegundos), el rendimiento de la prueba (medido de 0 a 100), LAS VENTAS (medidas en número de transacciones por mes), y así sucesivamente. Si no está seguro de si su variable dependiente es continua (es decir, medida en el nivel de intervalo o relación), consulte nuestra guía de tipos de variables.,
- suposición #2: Su variable independiente debe medirse a nivel continuo o categórico. Sin embargo, si tiene una variable independiente categórica, es más común usar una prueba t independiente (para 2 grupos) o ANOVA unidireccional (para 3 grupos o más). En caso de que no esté seguro, los ejemplos de variables categóricas incluyen el género (por ejemplo, 2 grupos: hombres y mujeres), el origen étnico (por ejemplo, 3 grupos: caucásicos, afroamericanos e hispanos), el nivel de actividad física (por ejemplo, 4 grupos: sedentario, bajo, moderado y alto) y la profesión (por ejemplo,,, 5 grupos: cirujano, médico, enfermera, dentista, terapeuta). En esta guía, le mostramos el procedimiento de regresión lineal y la salida de Stata cuando sus variables dependientes e independientes se midieron en un nivel continuo.
afortunadamente, puede verificar las suposiciones #3, #4, #5, #6 y #7 usando Stata. Al pasar a las suposiciones #3, #4, #5, #6 y # 7, sugerimos probarlos en este orden porque representa un orden donde, si una violación a la suposición no es corregible, ya no podrá usar regresión lineal., De hecho, no se sorprenda si sus datos fallan en una o más de estas suposiciones, ya que esto es bastante típico cuando se trabaja con datos del mundo real en lugar de ejemplos de libros de texto, que a menudo solo le muestran cómo llevar a cabo la regresión lineal cuando todo va bien. Sin embargo, no se preocupe porque incluso cuando sus datos fallan en ciertas suposiciones, a menudo hay una solución para superar esto (por ejemplo, transformar sus datos o usar otra prueba estadística en su lugar)., Solo recuerde que si no comprueba que sus datos cumplen con estas suposiciones o las Prueba incorrectamente, los resultados que obtiene al ejecutar la regresión lineal podrían no ser válidos.
- suposición # 3: debe haber una relación lineal entre las variables dependientes e independientes. Si bien hay varias formas de verificar si existe una relación lineal entre sus dos variables, sugerimos crear una gráfica de dispersión usando Stata, donde puede trazar la variable dependiente contra su variable independiente., A continuación, puede inspeccionar visualmente la gráfica de dispersión para comprobar la linealidad. Su gráfica de dispersión puede parecerse a una de las siguientes:
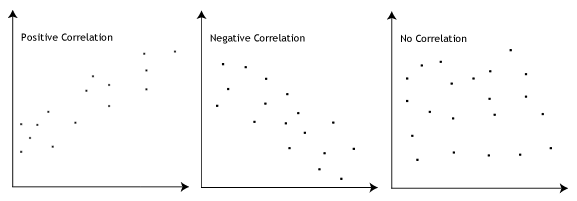
Si la relación mostrada en su gráfica de dispersión no es lineal, tendrá que ejecutar un análisis de regresión no lineal o «transformar» sus datos, lo que puede hacer usando Stata.
- suposición # 4: no debe haber valores atípicos significativos. Los valores atípicos son simplemente puntos de datos individuales dentro de sus datos que no siguen el patrón habitual (p. ej.,, en un estudio de las puntuaciones de CI de 100 estudiantes, donde la puntuación media fue de 108 con solo una pequeña variación entre los estudiantes, una estudiante tuvo una puntuación de 156, lo que es muy inusual, e incluso puede colocarla en el 1% superior de las puntuaciones de CI a nivel mundial). Las siguientes gráficas de dispersión destacan el impacto potencial de los valores atípicos:
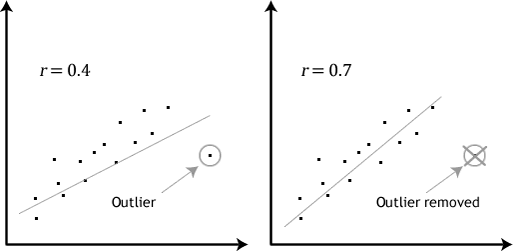
el problema con los valores atípicos es que pueden tener un efecto negativo en la ecuación de regresión que se utiliza para predecir el valor de la variable dependiente en función de la variable independiente., Esto cambiará el resultado que produce Stata y reducirá la precisión predictiva de sus resultados. Afortunadamente, puede usar Stata para llevar a cabo diagnósticos casewise que le ayuden a detectar posibles valores atípicos.
- suposición #5: debe tener independencia de las observaciones, que puede verificar fácilmente usando la estadística de Durbin-Watson, que es una prueba simple de ejecutar usando Stata.
- suposición # 6: sus datos deben mostrar homoscedasticidad, que es donde las variaciones a lo largo de la línea de mejor ajuste permanecen similares a medida que se mueve a lo largo de la línea., Las dos gráficas de dispersión a continuación proporcionan ejemplos simples de datos que cumplen con esta suposición y una que falla la suposición:
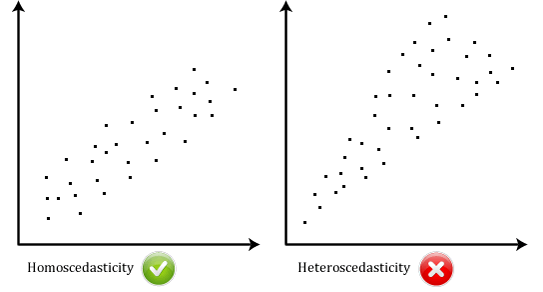
cuando analiza sus propios datos, tendrá suerte si su gráfica de dispersión se parece a cualquiera de los dos anteriores. Si bien estos ayudan a ilustrar las diferencias en los datos que cumplen o violan la suposición de homocedasticidad, los datos del mundo real a menudo son mucho más desordenados., Puede verificar si sus datos mostraron homocedasticidad trazando los residuos estandarizados de regresión contra el valor predicho estandarizado de regresión.
- suposición # 7: finalmente, debe verificar que los residuos (errores) de la línea de regresión estén distribuidos aproximadamente normalmente. Dos métodos comunes para verificar esta suposición incluyen el uso de un histograma (con una curva normal superpuesta) o una gráfica P-P Normal.
en la práctica, comprobando supuestos #3, #4, #5, #6 y #7 probablemente ocupará la mayor parte de su tiempo al llevar a cabo la regresión lineal., Sin embargo, no es una tarea difícil, y Stata proporciona todas las herramientas que necesita para hacerlo.
en la sección, Procedimiento, ilustramos el procedimiento stata requerido para realizar regresión lineal asumiendo que no se han violado las suposiciones. Primero, exponemos el ejemplo que usamos para explicar el procedimiento de regresión lineal en Stata.
stata
ejemplo
Los estudios muestran que el ejercicio puede ayudar a prevenir las enfermedades cardíacas. Dentro de límites razonables, cuanto más ejercicio haga, menos riesgo tendrá de sufrir una enfermedad cardíaca., Una forma en la que el ejercicio reduce el riesgo de sufrir una enfermedad cardíaca es mediante la reducción de una grasa en la sangre, llamada colesterol. Cuanto más ejercicio haga, menor será su concentración de colesterol. Además, recientemente se ha demostrado que la cantidad de tiempo que pasa viendo la televisión – un indicador de un estilo de vida sedentario – podría ser un buen predictor de enfermedad cardíaca (es decir, es decir, mientras más televisión vea, mayor será su riesgo de enfermedad cardíaca).,
Por lo tanto, un investigador decidió determinar si la concentración de colesterol estaba relacionada con el tiempo dedicado a ver la televisión en hombres de 45 a 65 años de edad sanos (Una categoría de personas en riesgo). Por ejemplo, a medida que las personas pasaban más tiempo viendo la televisión, ¿su concentración de colesterol también aumentó (una relación positiva) o sucedió lo contrario? El investigador también quería saber la proporción de concentración de colesterol que el tiempo dedicado a ver la televisión podría explicar, así como ser capaz de predecir la concentración de colesterol., El investigador podría entonces determinar si, por ejemplo, las personas que pasaron ocho horas viendo televisión por día tenían niveles peligrosamente altos de concentración de colesterol en comparación con las personas que ven solo dos horas de televisión.
para realizar el análisis, la investigadora reclutó a 100 participantes varones sanos entre las edades de 45 y 65 años. La cantidad de tiempo dedicado a ver la televisión (es decir, la variable independiente, time_tv) y la concentración de colesterol (es decir, la variable dependiente, colesterol) se registraron para los 100 participantes., Expresado en términos variables, el investigador quería retroceder el colesterol en time_tv.
Nota: el ejemplo y los datos utilizados para esta guía son ficticios. Acabamos de crearlos para los propósitos de esta guía.
Stata
Setup in Stata
Nota: No importa si primero crea la variable dependiente o independiente.
después de crear estas dos variables-time_tv y cholesterol – ingresamos las puntuaciones de cada una en las dos columnas de la hoja de cálculo del Editor de datos (Edit) (I. e.,, el tiempo en horas que los participantes vieron la televisión en la columna de la izquierda (es decir, time_tv, la variable independiente), y la concentración de colesterol de los participantes en mmol/L en la columna de la derecha (es decir, colesterol, la variable dependiente), como se muestra a continuación:
publicado con permiso por escrito de StataCorp LP.,
stata
procedimiento de prueba en Stata
en esta sección, le mostramos cómo analizar sus datos mediante regresión lineal en Stata cuando no se han violado las seis suposiciones de la sección anterior, suposiciones. Puede llevar a cabo la regresión lineal utilizando el código o la interfaz gráfica de usuario (GUI) de Stata. Después de haber realizado su análisis, le mostramos cómo interpretar sus resultados. En primer lugar, elija si desea utilizar el código o la interfaz gráfica de usuario (GUI) de Stata.,
Code
el código para llevar a cabo la regresión lineal en sus datos toma la forma:
regress DependentVariable IndependentVariable
Este código se introduce en el cuadro a continuación:
publicado con permiso por escrito de statacorp LP.,
Usando nuestro ejemplo donde la variable dependiente es colesterol y la variable independiente es time_tv, el código requerido sería:
regresar colesterol time_tv
Nota 1: debe ser preciso al ingresar el código en la casilla . El código es «sensible a mayúsculas y minúsculas». Por ejemplo, si introduce «Colesterol», donde la «C» mayúscula en lugar de minúsculas (es decir,,, una pequeña «c»), que debería ser, obtendrá un mensaje de error como el siguiente:
Nota 2: si todavía está recibiendo el mensaje de error en la nota 2: anterior, vale la pena verificar el nombre que le dio a sus dos variables en el Editor de datos cuando configuró su archivo (es decir, consulte la pantalla del Editor de datos anterior)., En el cuadro en el lado derecho de la pantalla del Editor de datos, es la forma en que escribe sus variables en la sección
, no la sección
la que necesita introducir en el código (consulte a continuación nuestra variable dependiente). Esto puede parecer obvio, pero es un error que a veces, lo que resulta en el error en la Nota 2 anterior.
por lo tanto, ingrese el código, retroceda cholesterol time_tv y presione el botón «Return/Enter» en su teclado.,
Publicado con el permiso por escrito de StataCorp LP.
puede ver la salida Stata que se producirá aquí.,
interfaz gráfica de usuario (GUI)
Los tres pasos necesarios para llevar a cabo la regresión lineal en Stata 12 y 13 se muestran a continuación:
- Click Statistics > modelos lineales y relacionados > regresión lineal en el menú principal, como se muestra a continuación:
publicado con permiso por escrito de statacorp LP.,
Se le presentará el cuadro de diálogo regresión-regresión lineal:
publicado con permiso por escrito de StataCorp LP.
- seleccione colesterol en el cuadro desplegable variable dependiente: y time_tv en el cuadro desplegable variables independientes:. Terminará con la siguiente pantalla:
publicado con permiso por escrito de StataCorp LP.,
-
haga Clic en el
botón. Esto generará la salida.
Stata
Salida del análisis de regresión lineal en Stata
Si sus datos pasaron la suposición #3 (es decir, hubo una relación lineal entre sus dos variables), #4 (es decir, no hubo valores atípicos significativos), la suposición #5 (es decir, tuvo independencia de las observaciones), la suposición #6 (es decir, sus datos mostraron homoscedasticidad) y la suposición #7 (i. e.,, los residuos (errores) se distribuyeron aproximadamente normalmente), que explicamos anteriormente en la sección de supuestos, solo tendrá que interpretar la siguiente salida de regresión lineal en Stata:
publicado con permiso por escrito de StataCorp LP.,
la salida consta de cuatro piezas importantes de información: (a) el valor R2 (fila»R-cuadrado») representa la proporción de varianza en la variable dependiente que puede ser explicada por nuestra variable independiente (técnicamente es la proporción de variación explicada por el modelo de regresión por encima y más allá del modelo medio). Sin embargo, R2 se basa en la muestra y es una estimación sesgada positivamente de la proporción de la varianza de la variable dependiente explicada por el modelo de regresión (i. e.,, es demasiado grande); (b) Un valor R2 AJUSTADO (fila»Adj R-cuadrado»), que corrige el sesgo positivo para proporcionar un valor que se esperaría en la población; (c) el valor F, grados de libertad («F( 1, 98)») y la significación estadística del modelo de regresión («Prob > f» fila); y (d) los coeficientes para la variable constante e independiente («Coef.»columna), que es la información que necesita para predecir la variable dependiente, colesterol, utilizando la variable independiente, time_tv.
En este ejemplo, R2 = 0.151. R2 AJUSTADO = 0,143 ( a 3 p. d.,), lo que significa que la variable independiente, time_tv, explica el 14,3% de la variabilidad de la variable dependiente, colesterol, en la población. R2 ajustado es también una estimación del tamaño del efecto, que en 0.143 (14.3%), es indicativo de un tamaño de efecto medio, de acuerdo con la clasificación de Cohen (1988). Sin embargo, normalmente es R2 no el R2 ajustado que se reporta en los resultados. En este ejemplo, el modelo de regresión es estadísticamente significativo, F (1, 98) = 17.47, p = .0001., Esto indica que, en general, el modelo aplicado puede predecir estadísticamente significativamente la variable dependiente, el colesterol.
Nota: presentamos la salida del análisis de regresión lineal anterior. Sin embargo, dado que debería haber probado sus datos para las suposiciones que explicamos anteriormente en la sección suposiciones, también deberá interpretar la salida de Stata que se produjo cuando probó estas suposiciones. Esto incluye: (a) las gráficas de dispersión que usó para verificar si había una relación lineal entre sus dos variables (i. e.,, Suposición #3); (B) diagnósticos casewise para verificar que no hubo valores atípicos significativos (es decir, suposición #4); (c) la salida de la estadística de Durbin-Watson para verificar la independencia de las observaciones (es decir, suposición #5); (d) una gráfica de dispersión de los residuos estandarizados de regresión contra el valor predicho estandarizado de regresión para determinar si sus datos mostraron homoscedasticidad (es decir, suposición #6); y un histograma (con curva normal superpuesta) y una gráfica P-P Normal para verificar si los residuos (errores) se distribuyeron aproximadamente normalmente (es decir, la suposición #7)., Además, recuerde que si sus datos fallaron en cualquiera de estas suposiciones, la salida que obtiene del procedimiento de regresión lineal (es decir, la salida que discutimos anteriormente) ya no será relevante, y es posible que tenga que llevar a cabo una prueba estadística diferente para analizar sus datos.,
Stata
Reporting the output of linear regression analysis
Cuando reporta el resultado de su regresión lineal, es una buena práctica incluir: (a) una introducción al análisis que realizó; (b) información sobre su muestra, incluyendo cualquier valor faltante; (c) el valor F observado, grados de libertad y nivel de significación (es decir, el valor p); (d) el porcentaje de la variabilidad en la variable dependiente explicada por la variable independiente (es decir, su R2 ajustado ); y (E) La ecuación de regresión para su modelo., Con base en los resultados anteriores, podríamos reportar los resultados de este estudio de la siguiente manera:
- general
una regresión lineal estableció que el tiempo diario dedicado a ver televisión podría predecir estadísticamente significativamente la concentración de colesterol, F(1, 98) = 17.47, p = .0001 y el tiempo dedicado a ver la televisión representaron el 14,3% de la variabilidad explicada en la concentración de colesterol. La ecuación de regresión fue: concentración predicha de colesterol = -2.135 + 0.044 x (tiempo dedicado a ver televisión).,
Además de informar los resultados como se indica anteriormente, se puede usar un diagrama para presentar visualmente sus resultados. Por ejemplo, podría hacer esto usando una gráfica de dispersión con confianza e intervalos de predicción (aunque no es muy común agregar el último). Esto puede hacer que sea más fácil para otros entender sus resultados. Además, puede usar su ecuación de regresión lineal para hacer predicciones sobre el valor de la variable dependiente en función de diferentes valores de la variable independiente., Si bien Stata no produce estos valores como parte del procedimiento de regresión lineal anterior, hay un procedimiento en Stata que puede usar para hacerlo.