clásicamente pensamos que la luz siempre viaja en líneas rectas, pero cuando las ondas de luz pasan cerca de una barrera tienden a doblarse alrededor de esa barrera y se extienden. La difracción de la luz ocurre cuando una onda de luz pasa por una esquina o a través de una abertura o hendidura que es físicamente del tamaño aproximado o incluso más pequeño que la longitud de onda de esa luz.,

se puede realizar una demostración muy simple de difracción sosteniendo su mano frente a una fuente de luz y cerrando lentamente dos dedos mientras observa la luz transmitida entre ellos. A medida que los dedos se acercan entre sí y se acercan mucho, se empieza a ver una serie de líneas oscuras paralelas a los dedos. Las líneas paralelas son en realidad patrones de difracción. Este fenómeno también puede ocurrir cuando la luz se» dobla » alrededor de partículas que están en el mismo orden de magnitud que la longitud de onda de la luz., Un buen ejemplo de esto es la difracción de la luz solar por las nubes que a menudo nos referimos como un lado positivo, ilustrado en la Figura 1 con una hermosa puesta de sol sobre el océano.
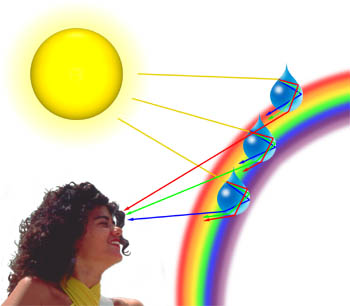
a menudo podemos observar tonos pastel de azul, rosa, púrpura y verde en las nubes que se generan cuando la luz se difracta de las gotas de agua en las nubes. La cantidad de difracción depende de la longitud de onda de la luz, con longitudes de onda más cortas difractadas en un ángulo mayor que las más largas (en efecto, la luz azul y violeta se difractan en un ángulo más alto que la luz roja)., Como una onda de luz que viaja a través de la atmósfera se encuentra con una gotita de agua, como se ilustra a continuación, primero se refracta en la interfaz de agua:aire, luego se refleja cuando se encuentra de nuevo con la interfaz. El haz, que todavía viaja dentro de la gota de agua, se refracta una vez más cuando golpea la interfaz por tercera vez. Esta última interacción con la interfaz refracta la luz de vuelta a la atmósfera, pero también difracta una parte de la luz como se ilustra a continuación., Este elemento de difracción conduce a un fenómeno conocido como halo de Cellini (también conocido como el efecto Heiligenschein) donde un anillo de luz brillante rodea la sombra de la cabeza del observador.
los Términos difracción y dispersión se usan a menudo indistintamente y se consideran casi sinónimos. La difracción describe un caso especializado de dispersión de luz en el que un objeto con características que se repiten regularmente (como una rejilla de difracción) produce una difracción ordenada de la luz en un patrón de difracción., En el mundo real, la mayoría de los objetos tienen una forma muy compleja y se debe considerar que están compuestos de muchas características de difracción individuales que pueden producir colectivamente una dispersión aleatoria de luz.
uno de los conceptos clásicos y más fundamentales que involucran la difracción es el experimento de difracción óptica de una sola rendija, realizado por primera vez a principios del siglo XIX. Cuando una onda de luz se propaga a través de una hendidura (o abertura) el resultado depende del tamaño físico de la abertura con respecto a la longitud de onda del haz incidente., Esto se ilustra en la Figura 3 suponiendo que una onda coherente y monocromática emitida desde la fuente puntual S, similar a la luz que sería producida por un láser, pasa a través de la abertura d y se difracta, con el haz de luz incidente primario aterrizando en el punto P y los primeros máximos secundarios ocurriendo en el punto Q.
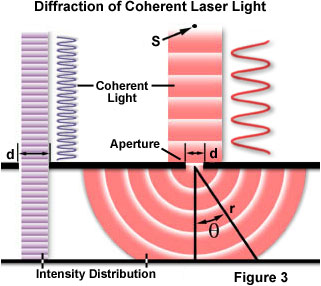
como se muestra en el lado izquierdo de la figura, cuando la longitud de onda (λ) es mucho menor que el ancho de apertura (d), la onda simplemente viaja hacia adelante en una línea recta, tal como lo haría si fuera una partícula o no estuviera presente ninguna abertura., Sin embargo, cuando la longitud de onda excede el tamaño de la abertura, experimentamos difracción de la luz de acuerdo con la ecuación:
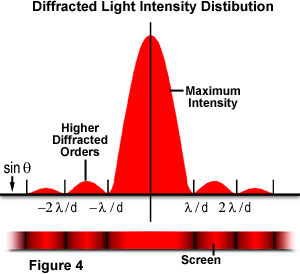
donde θ es el ángulo entre la dirección de propagación Central incidente y el primer mínimo del patrón de difracción. El experimento produce un máximo central brillante que está flanqueado en ambos lados por máximos secundarios, con la intensidad de cada máximo secundario posterior disminuyendo a medida que aumenta la distancia desde el centro. La figura 4 ilustra este punto con una gráfica de la intensidad del haz versus el radio de difracción., Tenga en cuenta que los mínimos que ocurren entre los máximos secundarios se encuentran en múltiplos de π.
Este experimento fue explicado por primera vez por Augustin Fresnel quien, junto con Thomas Young, produjo evidencia importante que confirma que la luz viaja en ondas. De las figuras anteriores, vemos cómo una luz coherente y monocromática (en este ejemplo, iluminación láser) emitida desde el punto L es difractada por la apertura d., Fresnel asumió que la amplitud de los máximos de primer orden en el punto Q (definido como eQ) estaría dada por la ecuación:
donde A es la amplitud de la onda incidente, r es la distancia entre D y Q, y f(χ) es una función de χ, un factor de inclinación introducido por Fresnel.
difracción de luz
Explore cómo se difracta un haz de luz cuando pasa a través de una ranura estrecha o abertura. Ajuste la longitud de onda y el tamaño de apertura y observe cómo esto afecta el patrón de intensidad de difracción.,
la difracción de la luz juega un papel primordial en la limitación del poder de resolución de cualquier instrumento óptico (por ejemplo: cámaras, binoculares, telescopios, microscopios y el ojo). El poder de resolución es la capacidad del instrumento óptico para producir imágenes separadas de dos puntos adyacentes. Esto a menudo está determinado por la calidad de las lentes y espejos en el instrumento, así como las propiedades del medio circundante (generalmente aire). La naturaleza ondulatoria de la luz fuerza un límite máximo al poder de resolución de todos los instrumentos ópticos.,
nuestras discusiones sobre difracción han utilizado una hendidura como la abertura a través de la cual se difracta la luz. Sin embargo, todos los instrumentos ópticos tienen aberturas circulares, por ejemplo, la pupila de un ojo o el diafragma circular y las lentes de un microscopio. Las aberturas circulares producen patrones de difracción similares a los descritos anteriormente, excepto que el patrón exhibe naturalmente una simetría circular. El análisis matemático de los patrones de difracción producidos por una apertura circular se describe mediante la ecuación:
donde θ (1) es la posición angular de los mínimos de difracción de primer orden (el primer anillo oscuro), λ es la longitud de onda de la luz incidente, d es el diámetro de la abertura, y 1.22 es una constante. En la mayoría de las circunstancias, el ángulo θ(1) es muy pequeño, por lo que la aproximación de que el sin y el tan del ángulo son casi iguales produce:
de estas ecuaciones se hace evidente que el máximo central es directamente proporcional a λ/d haciendo que este máximo se extienda más para longitudes de onda más largas y para aberturas más pequeñas., La mimina secundaria de difracción estableció un límite para la ampliación útil de las lentes objetivas en microscopía óptica, debido a la difracción inherente de la luz por estas lentes. No importa cuán perfecta sea la lente, la imagen de una fuente puntual de luz producida por la lente se acompaña de máximos secundarios y de orden superior. Esto solo podría eliminarse si la lente tuviera un diámetro infinito. Dos objetos separados por una distancia menor Que θ (1) no se pueden resolver, no importa cuán alto sea el poder de aumento., Si bien estas ecuaciones se derivaron para la imagen de una fuente puntual de luz a una distancia infinita de la abertura, es una aproximación razonable del poder de resolución de un microscopio cuando D se sustituye por el diámetro de la lente del objetivo.
por lo tanto, si dos objetos residen a una distancia D entre sí y están a una distancia L de un observador, el ángulo (expresado en radianes) entre ellos es:
lo que nos lleva a ser capaces de condensar las dos últimas ecuaciones para obtener:
donde D (0) es la distancia mínima de separación entre los objetos que permitirá resolverlos. Usando esta ecuación, el ojo humano puede resolver objetos separados por una distancia de 0.056 milímetros, sin embargo, los fotorreceptores en la retina no están lo suficientemente cerca entre sí para permitir este grado de resolución, y 0.1 milímetros es un número más realista en circunstancias normales.
el poder de resolución de los microscopios ópticos está determinado por una serie de factores, incluidos los discutidos, pero en las circunstancias más ideales, este número es de aproximadamente 0,2 micrómetros., Este número debe tener en cuenta La alineación óptica del microscopio, la calidad de las lentes, así como las longitudes de onda predominantes de la luz utilizada para la imagen de la muestra. Si bien a menudo no es necesario calcular el poder de resolución exacto de cada objetivo (y sería una pérdida de tiempo en la mayoría de los casos), es importante comprender las capacidades de las lentes del microscopio según se aplican al mundo real.
autores colaboradores
Mortimer Abramowitz – Olympus America, Inc., Two Corporate Center Drive., Melville, Nueva York, 11747.
Michael W., Davidson-National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.