FRANK K. MCKINNEY

la edad de los fósiles intriga a casi todos. Los estudiantes no solo quieren saber qué edad tiene un fósil, sino que también quieren saber cómo se determinó esa edad. Se utilizan algunos principios muy sencillos para determinar la edad de los fósiles. Los estudiantes deben ser capaces de entender los principios y tener eso como fondo para que las determinaciones de edad por paleontólogos y geólogos no parezcan magia negra.

Hay dos tipos de determinaciones de edad., Los geólogos de finales del siglo XVIII y principios del XIX estudiaron las capas de roca y los fósiles en ellas para determinar la edad relativa. William Smith fue uno de los científicos más importantes de esta época que ayudó a desarrollar el conocimiento de la sucesión de diferentes fósiles mediante el estudio de su distribución a través de la secuencia de rocas sedimentarias en el sur de Inglaterra. No fue hasta bien entrado el siglo 20 que se había acumulado suficiente información sobre la tasa de desintegración radiactiva que la edad de las rocas y los fósiles en número de años podría determinarse a través de la datación radiométrica de la edad.,

esta actividad sobre la determinación de la edad de rocas y fósiles está destinada a estudiantes de 8º o 9º grado. Se estima que requiere cuatro horas de clase, incluyendo aproximadamente una hora total de instrucción ocasional y explicación por parte del maestro y dos horas de grupo (equipo) y actividades individuales por parte de los estudiantes, más una hora de discusión entre los estudiantes dentro de los grupos de trabajo.,

Explore este enlace para obtener información adicional sobre los temas tratados en esta lección:

  • tiempo geológico

propósito y objetivos

esta actividad ayudará a los estudiantes a tener una mejor comprensión de los principios básicos utilizados para determinar la edad de las rocas y los fósiles. Esta actividad consta de varias partes. Los objetivos de esta actividad son:
1) hacer que los estudiantes determinen la edad relativa de un área geológicamente compleja. 2) familiarizar a los estudiantes con el concepto de vida media en la desintegración radiactiva.,
3) para que los estudiantes vean que las ejecuciones individuales de procesos estadísticos son menos predecibles que el promedio de muchas ejecuciones (o que las ejecuciones con números relativamente pequeños involucrados son menos confiables que las ejecuciones con muchos números).
4) para demostrar cómo se utiliza la tasa de desintegración radiactiva y la acumulación del producto de desintegración resultante en la datación radiométrica de rocas.

5) para usar la datación radiométrica y los principios de determinación de la edad relativa para mostrar cómo las edades de las rocas y los fósiles se pueden estrechar incluso si no se pueden fechar radiométricamente.,
volver al principio

materiales necesarios para cada grupo

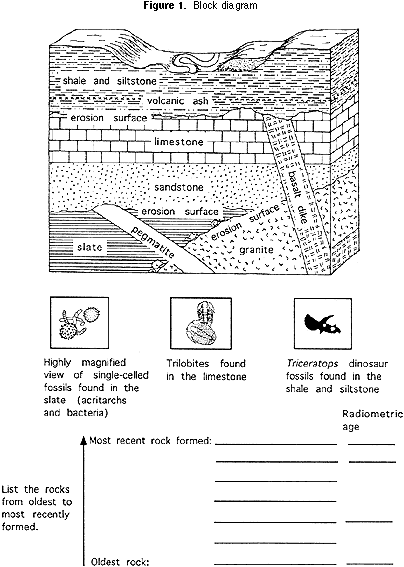
1) diagrama de bloques (Figura 1).
2) taza grande u otro recipiente en el que M & M Se puede agitar.
3) 100 M & M’s
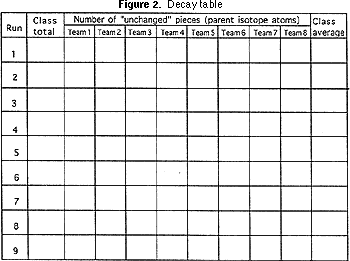
4) papel cuadriculado (Figura 2).
5) reloj o reloj que mantiene el tiempo a segundos. (Un solo reloj o reloj para toda la clase servirá.)
6) Pedazo de papel marcado tiempo e indicando ya sea 2, 4, 6, 8, o 10 minutos., 7) 128 tarjetas pequeñas o botones que pueden ser cortados de cartón o papel de construcción, preferiblemente con un color diferente en lados opuestos, cada uno marcado con «U-235» todo en un lado de color y «Pb-207» en el lado opuesto que tiene algún color de contraste.,



Volver a la parte superior

PARTE 1: DETERMINAR la EDAD RELATIVA DE las ROCAS

Cada equipo de 3 a 5 estudiantes deben discutir juntos cómo determinar la edad relativa de cada una de las unidades de roca en el diagrama de bloques (Figura 1). Después de que los estudiantes hayan decidido cómo establecer la edad relativa de cada unidad de roca, deben enumerarlos bajo el bloque, desde el más reciente en la parte superior de la lista hasta el más antiguo en la parte inferior.,

el profesor debe decirle a los estudiantes que hay dos principios básicos utilizados por los geólogos para determinar la secuencia de edades de las rocas. Son:
principio de superposición: las rocas sedimentarias más jóvenes se depositan sobre rocas sedimentarias más antiguas.principio de las relaciones transversales: cualquier rasgo geológico es más joven que cualquier otra cosa que atraviese.

parte 2: fechado radiométrico de la edad

algunos elementos tienen formas (llamadas isótopos) con núcleos atómicos inestables que tienen una tendencia a cambiar, o decaer., Por ejemplo, U-235 es un isótopo inestable de ofuranio que tiene 92 protones y 143 neutrones en el núcleo eus de cada átomo. A través de una serie de cambios dentro del núcleo, emite varias partículas, terminando con 82 protones y 125 neutrones. Esta es una condición estable, y no hay más cambios en el núcleo atómico. Un núcleo con ese número de protonsis llamado plomo (símbolo químico Pb). Los protones (82) y neutrones (125) totalizan 207. Esta forma particular (isótopo) de plomo se llama Pb-207. U-235 es el parentisótopo del Pb-207, que es el isótopo hija.,

muchas rocas contienen pequeñas cantidades de isótopos inestables y los isótopos hijos en los que se descomponen. Cuando las cantidades de isótopos padre e hijo pueden medirse con precisión, la relación puede usarse para determinar la edad de la roca, como se muestra en las siguientes actividades.

actividad de la parte 2a-en cualquier momento hay una pequeña posibilidad de que cada uno de los núcleos de U-235 decaiga repentinamente. Esa posibilidad de decaimiento es muy pequeña, pero siempre está presente y nunca cambia. En otras palabras, los núcleos no se» desgastan «ni se»cansan»., Si el núcleo aún no se ha descompuesto, siempre existe la misma posibilidad de que cambie en un futuro cercano.

los núcleos atómicos se mantienen unidos por una atracción entre las partículas nucleares grandes (protones y neutrones) que se conoce como la «fuerza nuclear fuerte», que debe exceder la repulsión electrostática entre los protones dentro del núcleo., En general, con la excepción del protón único que constituye el núcleo del isótopo más abundante de hidrógeno, el número de neutrones debe ser al menos igual al número de protones en un núcleo atómico, porque la repulsión electrostática prohíbe un empaque más denso de protones. Pero si hay demasiados neutrones, el núcleo es potencialmente inestable y se puede desencadenar la desintegración. Esto sucede en cualquier momento cuando la adición de la fugaz «fuerza nuclear débil» a la siempre presente repulsión electrostática excede la energía de unión requerida para mantener unido el núcleo.,

mediciones muy cuidadosas en laboratorios, hechas en un gran número de átomos de U-235, han demostrado que cada uno de los átomos tiene una probabilidad de 50:50 de decaer durante aproximadamente 704,000,000 años. En otras palabras, durante 704 millones de años, la mitad de los átomos de U-235 que existían al principio de ese tiempo decaerán a Pb-207. Esto se conoce como la vida media del U-235. Muchos elementos tienen algunos isótopos que son inestables, esencialmente porque tienen demasiados neutrones para ser equilibrados por el número de protones en el núcleo. Cada uno de estos isótopos inestables tiene su propia vida media característica., Algunas vidas medias tienen varios miles de millones de años, y otras son tan cortas como una diezmilésima de segundo.
volver al principio

una forma sabrosa para que los estudiantes entiendan acerca de la vida media es dar a cada equipo 100 piezas de «regular» m & m candy. En un trozo de papel de cuaderno, cada pieza debe colocarse con la M impresa hacia abajo. Esto representa el isótopo padre., El caramelo se debe verter en un recipiente lo suficientemente grande como para que reboten libremente, se debe agitar bien, luego se vierte de nuevo en el papel para que se extienda en lugar de hacer una pila. Esta primera vez de agitar representa una vida media, y todas esas piezas de caramelo que tienen la M impresa hacia arriba representan un cambio en el isótopo hija. El equipo debe recoger y dejar de lado solo los trozos de caramelo que tienen la M hacia arriba. Luego, cuenta el número de piezas de caramelo que quedan con la M hacia abajo., Estos son el isótopo padre que no cambió durante la primera semivida.

El profesor debe hacer que cada equipo informe cuántas piezas de isótopo padre quedan, y la primera fila de la tabla de decaimiento (Figura 2) debe rellenarse y calcularse el número promedio. El mismo procedimiento de agitar, contar los «sobrevivientes», y llenar la siguiente fila en la tabla de decaimiento debe hacerse siete u ocho veces más. Cada vez representa una vida media.

después de recoger los resultados de la «vida media» final del M& M, los caramelos ya no son necesarios.,

Cada equipo debe trazar en un gráfico (Figura 3) el número de piezas de caramelo que quedan después de cada uno de sus «batidos» y conectar cada punto sucesivo en el gráfico con una línea de luz. En el mismo gráfico, cada equipo debe trazar los valores promedio de la clase en su conjunto y conectarlos por una línea más pesada. Y, en el mismo gráfico, cada grupo debe trazar puntos donde, después de cada «sacudida» el número inicial se divide por exactamente dos y conectar estos puntos por una línea de diferente color. (Esta línea comienza en 100; el siguiente punto es 100 / 2, o 50; el siguiente punto es 50/2, o 25; y así sucesivamente.,)

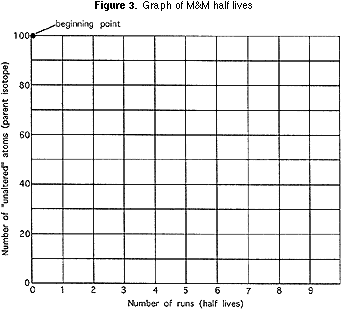después de trazar los gráficos, el profesor debe guiar a la clase a pensar en:
1) ¿por qué cada grupo no obtuvo los mismos resultados?
2) ¿Cuál sigue mejor la línea calculada matemáticamente? ¿Son los resultados de un solo grupo, o es la línea basada en el promedio de la clase? ¿Por qué?
3) ¿les fue más fácil a los estudiantes adivinar (predecir) los resultados cuando había muchos trozos de caramelo en la taza, o cuando había muy pocos? ¿Por qué?

U-235 se encuentra en la mayoría de las rocas ígneas., A menos que la roca se caliente a una temperatura muy alta, tanto el U-235 como su hija Pb-207 permanecen en la roca. Un geólogo puede comparar la proporción de átomos de U-235 con el PB-207 producido a partir de él y determinar la edad de la roca. La siguiente parte de este ejercicio muestra cómo se hace esto.
Volver arriba

parte 2b actividad — cada equipo recibe 128 piezas planas, con U-235 escrito en un lado y Pb-207 escrito en el otro lado. A cada equipo se le da un pedazo de papel marcado tiempo, en el que se escribe ya sea 2, 4, 6, 8, o 10 minutos.,

el equipo debe colocar cada pieza marcada para que aparezca «U-235″. Esto representa el uranio-235, que emite una serie de partículas desde el núcleo a medida que decae a plomo-207 (Pb-207). Cuando cada equipo esté listo con las 128 piezas mostrando» U-235″, un intervalo cronometrado de dos minutos debería comenzar. Durante ese tiempo, cada equipo entrega la mitad de las piezas del U-235 para que ahora muestren el Pb-207. Esto representa una «vida media» de U-235, que es el tiempo para que la mitad de los núcleos cambien del Padre U-235 al hijo PB-207.

comienza un nuevo intervalo de dos minutos., Durante este tiempo, el equipo debe entregar más de la mitad del U-235 que quedó después del primer intervalo de tiempo. Continuar con un total de 4 a 5 intervalos cronometrados.

sin embargo, cada equipo debe dejar de entregar piezas en el momento marcado en sus papeles de tiempo. Es decir, cada equipo debe detenerse de acuerdo con su papel de tiempo al final del primer intervalo cronometrado (2 minutos), o al final del segundo intervalo cronometrado (4 minutos), y así sucesivamente. Después de que todos los intervalos cronometrados hayan ocurrido, los equipos deben intercambiar lugares entre sí según las instrucciones del maestro., La tarea ahora para cada equipo es determinar cuántos intervalos cronometrados (es decir, cuántas semividas) ha experimentado el conjunto de piezas que están mirando.

la vida media de U-235 es de 704 millones de años. Tanto el equipo que entregó un conjunto de piezas como el segundo equipo que examinó el conjunto deben determinar cuántos millones de años están representados por la proporción de U-235 Y Pb-207 presentes, comparar notas y regatear sobre las diferencias que obtuvieron., (Derecha, cada equipo debe determinar el número de millones de años representados por el conjunto que ellos mismos entregaron, más el número de millones de años representados por el conjunto que otro equipo entregó.)

parte 3: poner fechas en rocas y fósiles

para el diagrama de bloques (Figura 1) al comienzo de este ejercicio, la relación de átomos de U-235:PB-207 en la pegmatita es 1:1, y su relación en el granito es 1:3. Usando el mismo razonamiento sobre las proporciones que en la parte 2B anterior, los estudiantes pueden determinar la edad de la pegmatita y el granito., Deben escribir las edades de la pegmatita y el granito junto a los nombres de las rocas en la lista debajo del diagrama de bloques (Figura 1).

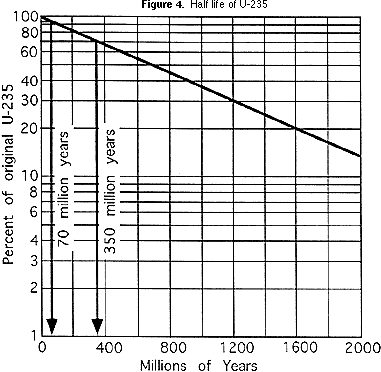
al trazar la vida media en un tipo de escala conocida como escala logarítmica, la línea curva como la de la actividad m & MTM se puede enderezar, como se puede ver en el gráfico de la Figura 4. Esto hace que la curva sea más útil, porque es más fácil trazarla con mayor precisión. Eso es especialmente útil para las proporciones de isótopo padre a isótopo hija que representan menos de una vida media., Para el diagrama de bloques (Figura 1), si un laboratorio geoquímico determina que la ceniza volcánica que se encuentra en la limolita tiene una relación de U-235:Pb-207 de 47:3 (94% de los restos originales de U-235), esto significa que la ceniza tiene 70 millones de años (ver Figura 4). Si la relación en el basalto es de 7:3 (70% de los restos originales de U-235), entonces el basalto tiene 350 millones de años (nuevamente, ver Figura 4). Los estudiantes deben escribir la edad de la ceniza volcánica junto al esquisto, limolita y basalto en la lista debajo del diagrama de bloques.,
volver al principio

preguntas para discusión

1) en función de las edades radiométricas disponibles, ¿puede determinar la edad posible de la unidad de roca que tiene acritarcas y bacterias? ¿Qué es eso? ¿Por qué no puedes decir exactamente cuál es la edad de la roca?
2) ¿se puede determinar la edad posible de la unidad de roca que tiene trilobites? ¿Qué es eso? ¿Por qué no puedes decir exactamente cuál es la edad de la roca?3) ¿Cuál es la edad de la roca que contiene los fósiles de Triceratops?, ¿Por qué puedes ser más preciso sobre la edad de esta roca que sobre las edades de la roca que tiene los trilobites y la roca que contiene acritarcas y bacterias?

Nota para profesores: basado en relaciones transversales, se estableció que la pegmatita es más joven que la pizarra y que la pizarra es más joven que el granito. Por lo tanto, la pizarra que contiene acritarca y bacterias tiene entre 704 millones y 1408 millones de años, porque la pegmatita tiene 704 millones de años y el granito tiene 1408 millones de años., La pizarra en sí no puede ser datada radiométricamente, por lo que solo puede ser entre corchetes entre las edades del granito y la pegmatita.

la piedra caliza que contiene trilobites cubre la piedra arenisca de cuarzo, Que corta en cruz la pegmatita, y el basalto corta a través de la piedra caliza. Por lo tanto, los trilobites y la roca que los contiene deben ser menores de 704 millones de años (la edad de la pegmatita) y mayores de 350 millones de años (la edad del basalto). La piedra caliza en sí no puede ser datada radiométricamente, por lo que solo puede ser entre corchetes entre las edades del granito y la pegmatita.,

Los fósiles de dinosaurio Triceratops tienen aproximadamente 70 millones de años, porque se encuentran en esquisto y limolita que contienen ceniza volcánica radiométricamente fechada a 70 millones de años. Cualquier Triceratops encontrado debajo de la ceniza volcánica puede ser un poco mayor de 70 millones de años, y cualquier encontrado arriba puede ser un poco menor de 70 millones de años., La edad del Triceratops se puede determinar más de cerca que la de los acritarcas y bacterias y la de los trilobites porque la unidad de roca que contiene el Triceratops se puede fechar radiométricamente, mientras que la de los otros fósiles no.