resistencias vs. inductores
Los inductores no se comportan de la misma manera que las resistencias. Mientras que las resistencias simplemente se oponen al flujo de corriente a través de ellas (cayendo un voltaje directamente proporcional a la corriente), los inductores se oponen a los cambios de corriente a través de ellas, cayendo un voltaje directamente proporcional a la tasa de cambio de corriente.
de acuerdo con la Ley de Lenz, este voltaje inducido es siempre de tal polaridad que intenta mantener la corriente en su Valor Actual., Es decir, si la corriente está aumentando en magnitud, el voltaje inducido » empujará contra «el flujo de corriente; si la corriente está disminuyendo, la polaridad se invertirá y» empujará con » la corriente para oponerse a la disminución.
esta oposición al cambio actual se llama reactancia, en lugar de resistencia., Expresada matemáticamente, la relación entre el voltaje caído a través del inductor y la tasa de cambio de corriente a través del inductor es como tal:

corriente alterna en un circuito inductivo simple
la expresión di/dt es una del cálculo, es decir, la tasa de cambio de la corriente instantánea (i) en el tiempo, en amperios por segundo.
la inductancia (L) está en Henrys, y el voltaje instantáneo (e), por supuesto, está en voltios., A veces encontrará la tasa de voltaje instantáneo expresada como» v «en lugar de» e » (v = L di/dt), pero significa exactamente lo mismo.
para mostrar lo que sucede con la corriente alterna, analicemos un circuito inductor simple:
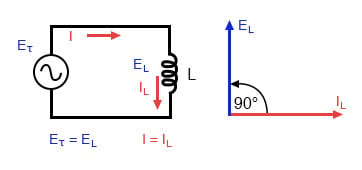
circuito inductivo puro: la corriente del Inductor retrasa el voltaje del inductor en 90°.
si tuviéramos que trazar la corriente y el voltaje para este circuito muy simple, se vería algo como esto:

circuito inductivo puro, formas de onda.,
recuerde, el voltaje caído a través de un inductor es una reacción contra el cambio en la corriente a través de él.
Por lo tanto, el voltaje instantáneo es cero cuando la corriente instantánea está en un pico (cambio cero, o pendiente de nivel, en la onda sinusoidal actual), y el voltaje instantáneo está en un pico donde la corriente instantánea está en el cambio máximo (los puntos de mayor pendiente en la onda actual, donde cruza la línea cero).
esto da como resultado una onda de voltaje que está 90° fuera de fase con la onda actual., Mirando el gráfico, la onda de voltaje parece tener una «ventaja» sobre la onda de corriente; el voltaje » conduce «la corriente y la corriente» se queda » detrás del voltaje.

la corriente retrasa el voltaje en 90° en un circuito inductivo puro.
las cosas se vuelven aún más interesantes cuando trazamos la potencia para este circuito:

en un circuito inductivo puro, la potencia instantánea puede ser positiva o negativa.,
debido a que la potencia instantánea es el producto de la tensión instantánea y la corriente instantánea (p=ie), la potencia es igual a cero cuando la corriente instantánea o el voltaje es cero. Cuando la corriente instantánea y el voltaje son positivos (por encima de la línea), la potencia es positiva.
al igual que con el ejemplo de resistencia, la potencia también es positiva cuando la corriente instantánea y el voltaje son negativos (por debajo de la línea).,
sin embargo, debido a que las ondas de corriente y voltaje están 90° fuera de fase, hay momentos en que una es positiva mientras que la otra es negativa, lo que resulta en ocurrencias igualmente frecuentes de potencia instantánea negativa.
¿qué es la potencia negativa?
pero ¿qué significa poder negativo? Significa que el inductor está liberando energía al circuito, mientras que una potencia positiva significa que está absorbiendo energía del circuito.,
dado que los ciclos de potencia positivos y negativos son iguales en magnitud y duración a lo largo del tiempo, el inductor libera tanta potencia al circuito como absorbe durante el lapso de un ciclo completo.
lo que esto significa en un sentido práctico es que la reactancia de un inductor disipa la energía neta de cero, muy a diferencia de la resistencia de una resistencia, que disipa la energía en forma de calor. Eso sí, esto es solo para inductores perfectos, que no tienen resistencia de alambre.
Reactancia vs, Resistencia
la oposición de un inductor al cambio de corriente se traduce en una oposición a la corriente alterna en general, que por definición siempre cambia en magnitud y dirección instantánea.
esta oposición a la corriente alterna es similar a la resistencia, pero diferente en que siempre resulta en un cambio de fase entre la corriente y el voltaje, y disipa la potencia cero. Debido a las diferencias, tiene un nombre diferente: reactancia. La reactancia A AC se expresa en ohmios, al igual que la resistencia, excepto que su símbolo matemático es X en lugar de R.,
para ser específicos, la reactancia asociada con un inductor generalmente se simboliza con la letra mayúscula X con una letra L como subíndice, como esto: XL.
dado que los inductores caen voltaje en proporción a la tasa de cambio de corriente, caerán más voltaje para corrientes de cambio más rápido, y menos voltaje para corrientes de cambio más lento. Lo que esto significa es que la reactancia en ohmios para cualquier inductor es directamente proporcional a la frecuencia de la corriente alterna., La fórmula exacta para determinar la reactancia es la siguiente:

Si exponemos un inductor de 10 mH a frecuencias de 60, 120 y 2500 Hz, manifestará las reactancias en la tabla siguiente.
Reactancia de un 10 mH inductor:
| Frecuencia (Hertz) | Reactancia (Ohmios) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
en la ecuación de reactancia, el término» 2nf » (todo en el lado derecho excepto la L) tiene un significado especial en sí mismo. Es el número de radianes por segundo en el que la corriente alterna está «girando», si imaginas un ciclo de CA para representar la rotación de un círculo completo.
un radián es una unidad de medida angular: hay 2π radianes en un círculo completo, al igual que hay 360° en un círculo completo., Si el alternador que produce la CA es una unidad del doble-polo, producirá un ciclo para cada vuelta completa de la rotación del eje, que es cada radianes 2π, o 360°.
si esta constante de 2π se multiplica por la frecuencia en Hertz (ciclos por segundo), el resultado será una figura en radianes por segundo, conocida como la velocidad angular del sistema AC.
Velocidad Angular en sistemas AC
La velocidad Angular puede ser representada por la expresión 2nf, o puede ser representada por su propio símbolo, la letra griega minúscula omega, que parece similar a nuestra «w» minúscula Romana: ω., Por lo tanto, la fórmula de reactancia XL = 2NFL también podría escribirse como XL = wL.
debe entenderse que esta «Velocidad angular» es una expresión de la rapidez con la que las formas de onda AC están en ciclo, un ciclo completo es igual a 2π radianes. No es necesariamente representativo de la velocidad real del eje del alternador que produce la CA.
si el alternador tiene más de dos polos, la velocidad angular será un múltiplo de la velocidad del eje., Por esta razón, ω A veces se expresa en unidades de radianes eléctricos por segundo en lugar de radianes (simples) por segundo, para distinguirlo del movimiento mecánico.
de cualquier forma que expresemos la velocidad angular del sistema, es evidente que es directamente proporcional a la reactancia en un inductor. A medida que aumenta la frecuencia (o la velocidad del eje del alternador) en un sistema de ca, un inductor ofrecerá una mayor oposición al paso de corriente, y viceversa.,
La corriente alterna en un circuito inductivo simple es igual a la tensión (en voltios) dividida por la reactancia inductiva (en ohmios), al igual que la corriente alterna o continua en un circuito resistivo simple es igual a la tensión (en voltios) dividida por la resistencia (en ohmios). Un ejemplo de circuito se muestra a continuación:

reactancia Inductiva

los Ángulos de Fase
sin Embargo, debemos tener en cuenta que el voltaje y la corriente no están en fase., Como se mostró anteriormente, el voltaje tiene un desplazamiento de fase de +90° con respecto a la corriente. Si representamos estos ángulos de fase de voltaje y corriente matemáticamente en forma de números complejos, encontramos que la oposición de un inductor a la corriente también tiene un ángulo de fase:


90° en un inductor.
matemáticamente, decimos que el ángulo de fase de la oposición de un inductor a la corriente es de 90°, lo que significa que la oposición de un inductor a la corriente es una cantidad imaginaria positiva., Este ángulo de fase de oposición reactiva a la corriente se vuelve críticamente importante en el análisis de circuitos, especialmente para circuitos de CA complejos donde la reactancia y la resistencia interactúan.
resultará beneficioso representar la oposición de cualquier componente a la corriente en términos de números complejos en lugar de cantidades escalares de resistencia y reactancia.
revisión:
- la reactancia inductiva es la oposición que un inductor ofrece a la corriente alterna debido a su almacenamiento desplazado de fase y liberación de energía en su campo magnético., La reactancia está simbolizada por la letra mayúscula «X» y se mide en ohmios al igual que la resistencia (R).
- la reactancia inductiva se puede calcular usando esta fórmula: XL = 2NFL
- La velocidad angular de un circuito de CA es otra forma de expresar su frecuencia, en unidades de radianes eléctricos por segundo en lugar de ciclos por segundo. Está simbolizado por la letra griega minúscula «omega», o ω.
- la reactancia inductiva aumenta con frecuencia creciente. En otras palabras, cuanto mayor sea la frecuencia, más se opone al flujo de electrones AC.,
hojas de Trabajo relacionadas:
- Hoja de trabajo de inductores
- Hoja de trabajo de reactancia inductiva