Variansen måler, hvor langt et sæt af data, der er spredt ud. En varians på nul indikerer, at alle dataværdierne er identiske. Alle ikke-nul afvigelser er positive.

en lille varians indikerer, at datapunkterne har en tendens til at være meget tæt på gennemsnittet og til hinanden., En høj varians indikerer, at datapunkterne er meget spredt ud fra gennemsnittet og fra hinanden. Varians er gennemsnittet af de kvadrerede afstande fra hvert punkt til middelværdien.

processen med at finde variansen svarer meget til at finde den gale, gennemsnitlige absolutte afvigelse.
Den eneste forskel er kvadrering af afstande.
proces: (1) Find middelværdien (gennemsnittet) af sættet. (2) Træk hver dataværdi fra middelværdien for at finde dens afstand fra middelværdien. (3) firkant alle afstande. (4) Tilføj alle kvadrater af afstande., (4) divider med antallet af data (for populationsvarians).

et problem med variansen er, at den ikke har den samme måleenhed som de oprindelige data. For eksempel har originale data, der indeholder længder målt i fødder, en varians målt i kvadratfod.,

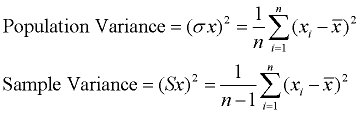Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Hvis du beregner manuelt, skal du altid have flere decimaler inden for beregningerne end forventet for det endelige resultat. Hvis du arbejder med en lommeregner, skal du bære den fulde værdi af lommeregnerens poster, indtil du når det endelige resultat.

standardafvigelsen viser, hvor stor variationen (spredning, spredning, scatter) fra middelværdien eksisterer., Det repræsenterer en “typisk” afvigelse fra middelværdien. Det er et populært mål for variabilitet, fordi det vender tilbage til de originale måleenheder for datasættet.

en lav standardafvigelse indikerer, at datapunkterne har en tendens til at være meget tæt på gennemsnittet. En høj standardafvigelse indikerer, at datapunkterne er spredt ud over en lang række værdier.
standardafvigelsen kan betragtes som en “standard” måde at vide, hvad der er normalt (typisk), hvad der er meget stort, og hvad der er meget lille i datasættet.,

standardafvigelse er et populært mål for variabilitet, fordi det vender tilbage til de oprindelige måleenheder for datasættet. For eksempel har originale data, der indeholder længder målt i fødder, en standardafvigelse, der også måles i fødder.,

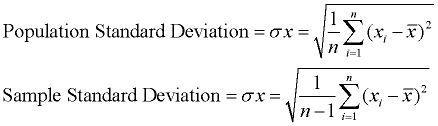for At beregne standardafvigelsen ved hånden:
standardafvigelsen er simpelthen kvadratroden af variansen.
denne beskrivelse er beregnet til beregning af populationsstandardafvigelse. Hvis prøvestandardafvigelse er nødvendig, divideres med n-1 i stedet for n., Da standardafvigelse er kvadratroden af variansen, skal vi først beregne variansen.
1. Find middelværdien.
2. Træk gennemsnittet fra hver dataværdi og firkant hver af disse forskelle (de kvadrerede forskelle).
3. Find gennemsnittet af de firkantede forskelle (tilføj dem og divider med antallet af dataværdier). Dette vil være variansen.,

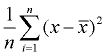varians
4. Tag kvadratroden. Dette vil være befolkningens standardafvigelse. Rund svaret i henhold til anvisningerne i problemet.

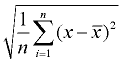standard afvigelse

Normal Kurve

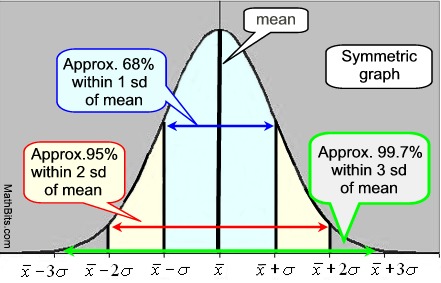
En normal kurven er symmetrisk, klokkeformede kurve., Midten af grafen er middelværdien, og højden og bredden af grafen bestemmes af standardafvigelsen. Når standardafvigelsen er lille, kurven vil være høj og smal i spredning. Når standardafvigelsen er stor, vil kurven være kort og bred i spredning. Middelværdien og medianen har samme værdi i en normal kurve.

Normal Kurve Empiriske Regel:
Ca …68% af dataene ligger inden for en standardafvigelse af middelværdien.,95% af dataene ligger inden for to standardafvigelser af gennemsnittet.99, 7% af dataene ligger inden for tre standardafvigelser af gennemsnittet.

i IR for en normal kurve er 1.34896 standard standardafvigelse.