Antagelse om normalitet i den afhængige variabel
Den uafhængige t-test kræver, at den afhængige variabel er tilnærmelsesvis normalt fordelt inden for hver gruppe.
Bemærk: teknisk set er det de rester, der skal distribueres normalt, men for en uafhængig t-test vil begge give dig det samme resultat.,
Du kan teste for dette ved hjælp af en række forskellige tests, men Shapiro-.ilks-testen af normalitet eller en grafisk metode, såsom et Plot -. – Plot, er meget almindelige. Du kan køre disse tests ved hjælp af SPSS statistik, den procedure, som kan findes i vores Testing for Normality guide. Imidlertid beskrives t-testen som en robust test med hensyn til antagelsen om normalitet. Dette betyder, at en vis afvigelse væk fra normalitet ikke har stor indflydelse på Type i-fejlfrekvenser. Undtagelsen til dette er, hvis forholdet mellem den mindste og største gruppestørrelse er større end 1.,5(største i forhold til mindste).
Hvad gør man, når man overtræder den normale antagelse
Hvis du opdager, at enten en eller begge af dine group ‘ s data er ikke tilnærmelsesvis normalt fordelt og grupper, størrelser varierer meget, har du to muligheder: (1) transform dine data, således at data bliver normalt fordelt (for at gøre dette i SPSS Statistics se vores vejledning om Omdannelse af Data), eller (2) køre Mann-Whitney U-test, som er en ikke-parametrisk test, der ikke kræver, at antagelsen om normalitet (til at køre denne test i SPSS Statistics se vores guide på Mann-Whitney U Test).,
antagelse af homogenitet af varians
den uafhængige t-test antager, at afvigelserne for de to grupper, du måler, er ens i befolkningen. Hvis dine afvigelser er ulige, kan dette påvirke Type i-fejlfrekvensen. Antagelsen om homogenitet af varians kan testes ved hjælp af Levenes Test af ligestilling af afvigelser, som produceres i SPSS-statistikker, når den uafhængige t-testprocedure køres., Hvis du har kørt Levene ‘ s Test af Lighed af Varianserne i SPSS Statistics, vil du få et resultat svarende til det, der nedenfor:

Denne test for homogenitet af variansen giver en F-statistik og en signifikans-værdi (p-værdi). Vi er primært optaget af signifikansværdien-hvis den er større end 0,05 (dvs .p >.05), kan vores gruppe afvigelser behandles som lige. Men hvis p < 0.05, har vi ulige afvigelser, og vi har overtrådt antagelsen om homogenitet af afvigelser.,
Overvinde en krænkelse af den antagelse af homogenitet af variansen
Hvis Levene ‘ s Test for Lighed af Varianserne er statistisk signifikant, hvilket indikerer, at gruppen varianserne er ulige i befolkningen, kan du korrigere for denne krænkelse, som ikke bruger de samlede estimat for fejlen udtrykket for t-statistikken, men i stedet ved hjælp af en justering i forhold til de grader af frihed ved hjælp af Welch-Satterthwaite metode., I virkeligheden, vil du sandsynligvis aldrig har hørt om disse justeringer, fordi SPSS Statistics skjuler disse oplysninger, og blot etiketter de to muligheder som “ens varianser antaget” og “Lige varians ikke antaget” uden udtrykkelig angivelse af den underliggende test, der anvendes., Dog, kan du se dokumentationen for disse tests som nedenfor:
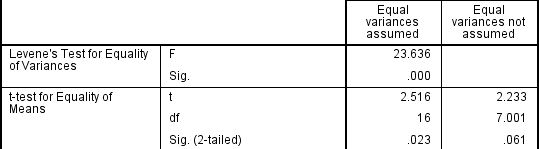
resultatet af Levene ‘ s Test for Lighed af Varianserne, kan vi afvise nulhypotesen om, at der ikke er nogen forskel på forskelle mellem grupper og acceptere den alternative hypotese, at der er en statistisk signifikant forskel i varianserne mellem grupper., Effekten af ikke at kunne antage lige afvigelser er tydelig i den sidste kolonne i ovenstående figur, hvor vi ser en reduktion i værdien af t-statistikken og en stor reduktion i frihedsgraderne (df). Dette har den virkning at øge p-værdien over det kritiske signifikansniveau på 0,05. I dette tilfælde accepterer vi derfor ikke den alternative hypotese og accepterer, at der ikke er statistisk signifikante forskelle mellem midler. Dette ville ikke have været vores konklusion, hvis vi ikke havde testet for homogenitet af afvigelser.