Support Vector Machine eller SVM er en af de mest populære overvågede læringsalgoritmer, der bruges til klassificering såvel som Regressionsproblemer. Men primært, det bruges til klassificering problemer i Machine Learning.
målet med SVM-algoritmen er at skabe den bedste linje eller beslutningsgrænse, der kan adskille n-dimensionelt rum i klasser, så vi nemt kan sætte det nye datapunkt i den rigtige kategori i fremtiden., Denne bedste beslutning grænse kaldes en hyperplan.
SVM vælger de ekstreme punkter / vektorer, der hjælper med at skabe hyperplanet. Disse ekstreme tilfælde kaldes som support vektorer, og dermed algoritme betegnes som Support vektor maskine. Overveje nedenstående diagram, hvor der er to forskellige kategorier, der er klassificeret ved hjælp af en beslutning grænse eller hyperplane:
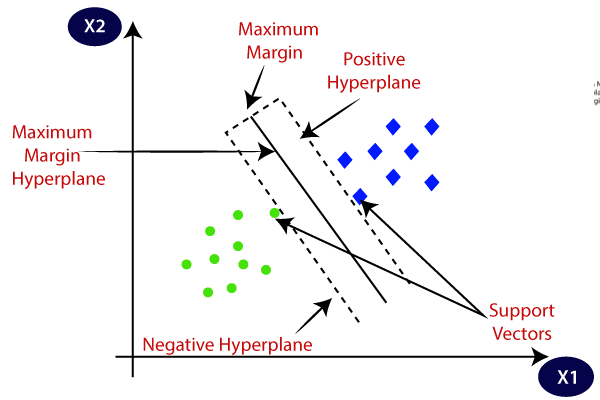
Eksempel: SVM kan forstås med det eksempel, som vi har brugt i KNN klassificeringen., Antag, at vi ser en mærkelig kat, der også har nogle funktioner hos hunde, så hvis vi vil have en model, der nøjagtigt kan identificere, om det er en kat eller en hund, så kan en sådan model oprettes ved hjælp af SVM-algoritmen. Vi vil først træne vores model med masser af billeder af katte og hunde, så den kan lære om forskellige funktioner hos katte og hunde, og så tester vi den med denne mærkelige væsen. Så som støtte vektor skaber en beslutning grænse mellem disse to data (kat og hund) og vælge ekstreme tilfælde (støtte vektorer), vil det se det ekstreme tilfælde af kat og hund., På basis af støttevektorerne vil den klassificere den som en kat. Overvej nedenstående diagram:
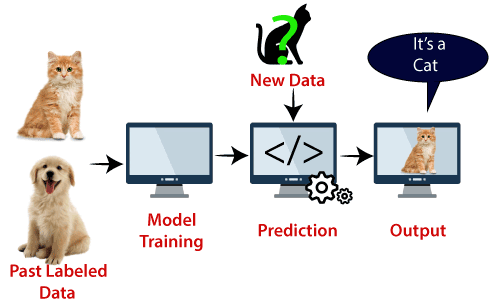
SVM-algoritme kan bruges til ansigtsgenkendelse, billedklassificering, tekstkategorisering osv.
typer af SVM
SVM kan være af to typer:
- lineær SVM: lineær SVM bruges til lineært adskillelige data, hvilket betyder, at hvis et datasæt kan klassificeres i to klasser ved hjælp af en enkelt lige linje, betegnes sådanne data som lineært adskillelige data, og klassifikator bruges kaldet som lineær SVM-klassifikator.,
- ikke-lineær SVM: ikke-lineær SVM bruges til ikke-lineært adskilte data, hvilket betyder, at hvis et datasæt ikke kan klassificeres ved hjælp af en lige linje, betegnes sådanne data som ikke-lineære data, og den anvendte klassifikator kaldes som ikke-lineær SVM-klassifikator.
Hyperplane og Støtte Vektorer i SVM algoritme:
Hyperplane: Der kan være flere linier/beslutning grænser til at adskille klasser i n-dimensionelle rum, men vi er nødt til at finde ud af den bedste beslutning grænse, der hjælper til at klassificere data punkter. Denne bedste grænse er kendt som HYPERPLANE af SVM.,
dimensionerne af hyperplanet afhænger af de funktioner, der findes i datasættet, hvilket betyder, at hvis der er 2 funktioner (som vist på billedet), vil hyperplan være en lige linje. Og hvis der er 3 funktioner, vil hyperplan være et 2-dimensionsplan.
Vi opretter altid et hyperplan, der har en maksimal margen, hvilket betyder den maksimale afstand mellem datapunkterne.
Supportvektorer:
datapunkterne eller vektorerne, der er tættest på hyperplanet, og som påvirker hyperplanets position, betegnes som Supportvektor., Da disse vektorer understøtter hyperplanet, kaldes det derfor en Støttevektor.
Hvordan virker SVM?
lineær SVM:
arbejdet med SVM-algoritmen kan forstås ved hjælp af et eksempel. Antag, at vi har et datasæt, der har to tags (grøn og blå), og datasættet har to funktioner11 og22. Vi ønsker en klassifikator, der kan klassificere parret (11, .2) af koordinater i enten grøn eller blå. Overvej nedenstående billede:
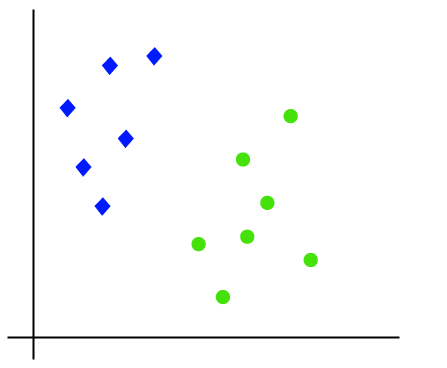
så som det er 2-D plads så ved blot at bruge en lige linje, kan vi nemt adskille disse to klasser., Men der kan være flere linjer, der kan adskille disse klasser. Overvej nedenstående billede:
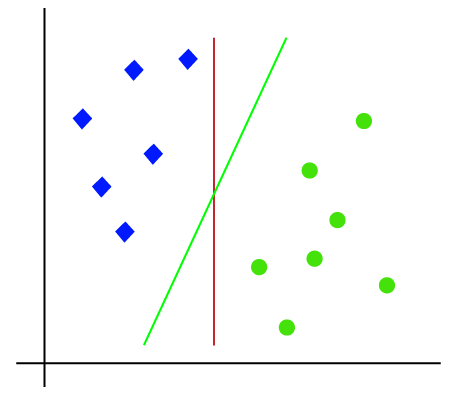
derfor hjælper SVM-algoritmen med at finde den bedste linje eller beslutningsgrænse; denne bedste grænse eller region kaldes som en hyperplan. SVM-algoritmen finder det nærmeste punkt på linjerne fra begge klasser. Disse punkter kaldes støttevektorer. Afstanden mellem vektorer og hyperplan kaldes som margin. Og målet med SVM er at maksimere denne margen. Hyperplanet med maksimal margen kaldes den optimale hyperplan.,
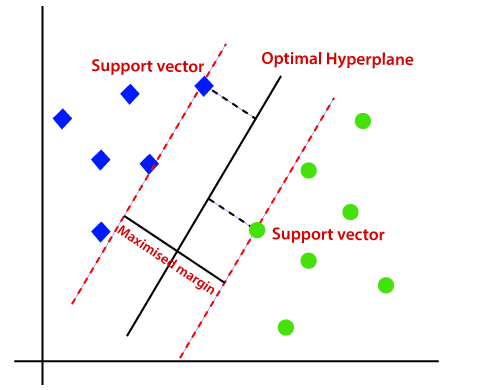
ikke-lineær SVM:
Hvis data er lineært arrangeret, kan vi adskille dem ved hjælp af en lige linje, men for ikke-lineære data kan vi ikke tegne en enkelt lige linje. Overvej nedenstående billede:
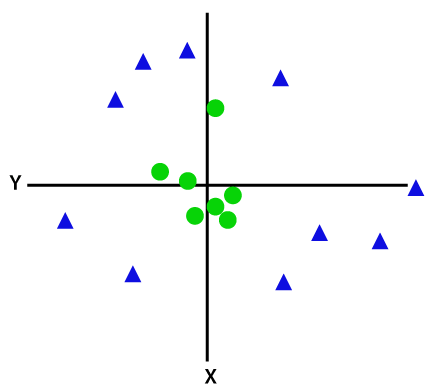
så for at adskille disse datapunkter skal vi tilføje endnu en dimension. For lineære data har vi brugt to dimensioner and og y, så for ikke-lineære data tilføjer vi en tredje dimension.., Det kan beregnes som:
z=x2 +y2
Ved at tilføje den tredje dimension, som prøven plads bliver som nedenstående billede:
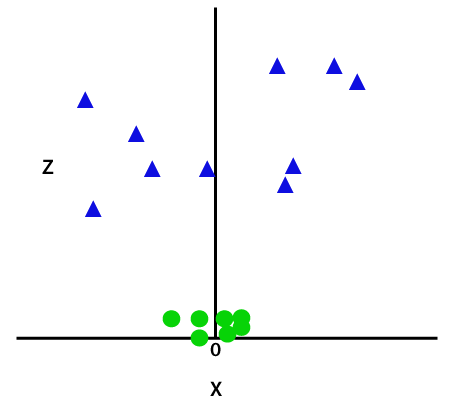
Så nu, SVM vil opdele datasættet i grupper på følgende måde. Overvej nedenstående billede:
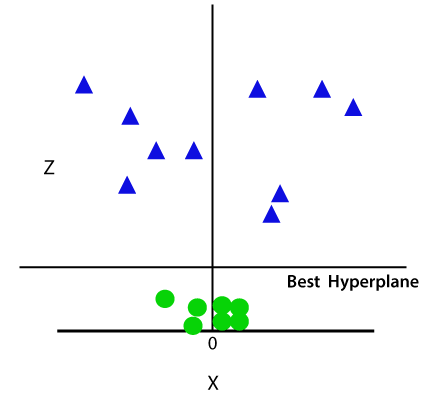
da vi er i 3-D-rum, ser det derfor ud som et plan parallelt med. – aksen. Hvis vi konverterer det i 2d-rum med.=1, bliver det som:
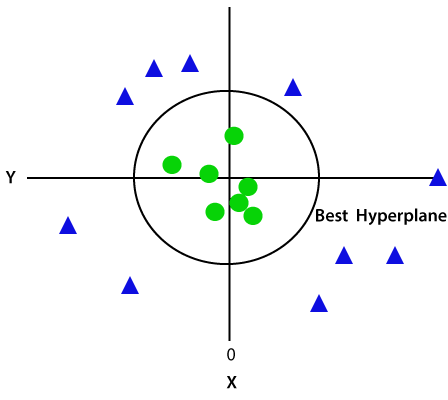
derfor får vi en omkreds af radius 1 i tilfælde af ikke-lineære data.,
Python implementering af Support Vector Machine
nu implementerer vi SVM-algoritmen ved hjælp af Python. Her bruger vi det samme datasæt user_data, som vi har brugt i logistisk regression og KNN-klassificering.
- data Forbehandlingstrin
indtil data forbehandlingstrinnet forbliver koden den samme. Nedenfor er koden:
Når du har udført ovenstående kode, vil vi forbehandle dataene., Koden giver datasættet som:
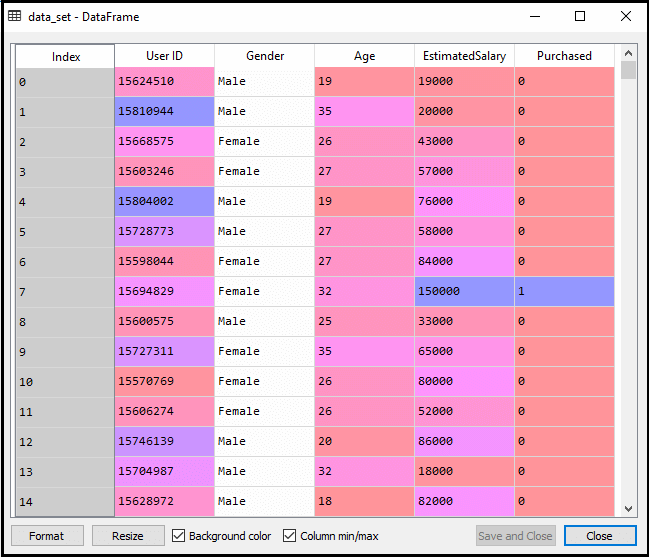
den skalerede udgang for testsættet vil være:
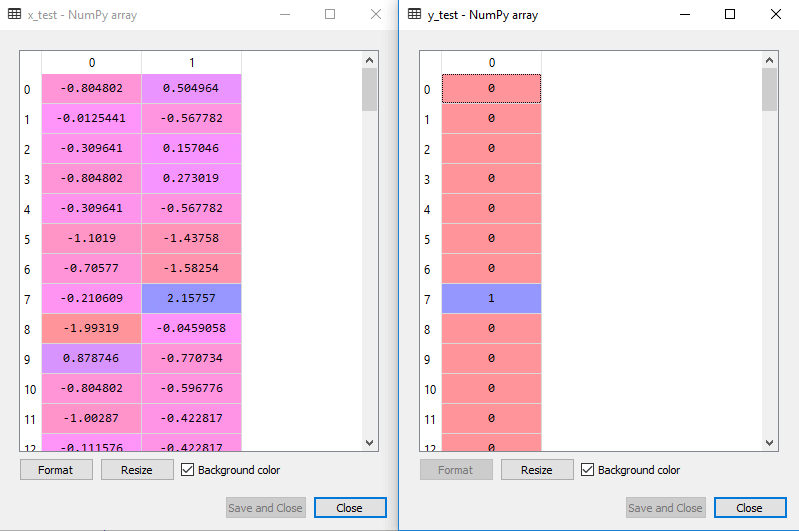
montering af SVM-klassifikatoren på træningssættet:
nu monteres træningssættet på SVM-klassifikatoren. For at oprette SVM-klassifikatoren importerer vi SVC-klasse fra Sklearn.svm bibliotek. Nedenfor er koden til den:
i ovenstående kode har vi brugt kernel=’lineær’, da vi her opretter SVM til lineært adskillelige data. Vi kan dog ændre det til ikke-lineære data., Og så har vi monteret klassificeringen til uddannelse datasæt(x_train, y_train)
Output:
model performance kan ændres ved at ændre værdien af C(Positive faktor), gamma, og kernen.
- forudsigelse af testsættets resultat:
nu vil vi forudsige output for testsæt. Til dette opretter vi en ny vektor y_pred. Nedenfor er koden for den:
efter at have fået y_pred-vektoren, kan vi sammenligne resultatet af y_pred og y_test for at kontrollere forskellen mellem den faktiske værdi og den forudsagte værdi.,
Output: Nedenfor er output til forudsigelse af den test, der:

- at Skabe forvirring matrix:
Nu vil vi se resultater af SVM klassificeringen, at så mange forkerte forudsigelser er der i forhold til den Logistiske regression klassificeringen. For at oprette forvirringsmatri theen skal vi importere confusion_matri. – funktionen i sklearn-biblioteket. Efter import af funktionen kalder vi den ved hjælp af en ny variabel cm. Funktionen tager to parametre, hovedsageligt y_true (de faktiske værdier) og y_pred (den målrettede værdiretur af klassifikatoren)., Nedenfor er koden for det:
Output:
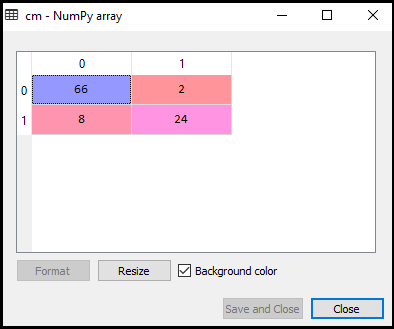
Som vi kan se i ovenstående output-billede, der er 66+24= 90 korrekte forudsigelser og 8+2= 10 korrekte forudsigelser. Derfor kan vi sige, at vores SVM-model forbedrede sig sammenlignet med den logistiske regressionsmodel.,
- Visualisere den erhvervsuddannelse, der er resultatet:
Nu vil vi visualisere uddannelse resultat, nedenfor er koden for det:
Output:
Ved at udføre ovenstående kode, vil vi få output som:
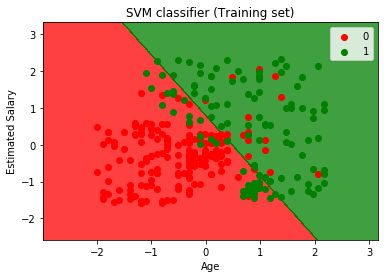
Som vi kan se, ovenstående output er der svarende til den Logistiske regression output. I output fik vi den lige linje som hyperplan, fordi vi har brugt en lineær kerne i klassifikatoren. Og vi har også diskuteret ovenfor, at for 2D-rummet er hyperplanet i SVM en lige linje.,
- Visualisering af test resultat:
Output:
Ved at udføre ovenstående kode, vil vi få output som:
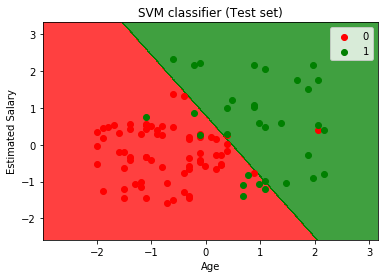
Som vi kan se i ovenstående output billede, den SVM klassificeringen har inddelt brugerne i to regioner (Købt eller Ikke købt). Brugere, der har købt SUV er i den røde region med de røde scatter punkter. Og brugere, der ikke købte SUV ‘ en, er i den grønne region med grønne spredningspunkter. Hyperplanen har opdelt de to klasser i købt og ikke købt variabel.