beregning af området under en kurve.
bestemte integraler
indtil videre, når man integrerer, har der altid været et konstant udtryk tilbage. Af denne grund er sådanne integraler kendt som ubestemt integraler. Med bestemte integraler integrerer vi en funktion mellem 2 point, og så kan vi finde den nøjagtige værdi af integralet, og der er ikke behov for ukendte konstante vilkår .,

Arealet Under en Kurve
arealet under en kurve mellem to punkter kan findes ved at gøre en bestemt integral mellem de to punkter.
for at finde området under kurven y = f (.) mellem y = A og and = b skal du integrere y = f (.) mellem grænserne for a og b.
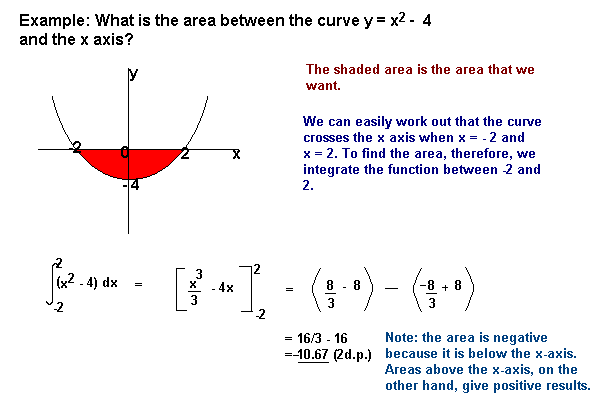
områder under axis-aksen vil komme ud negativt, og områder over.-aksen vil være positive. Det betyder, at du skal være forsigtig, når du finder et område, der er dels over og dels under x-aksen.,
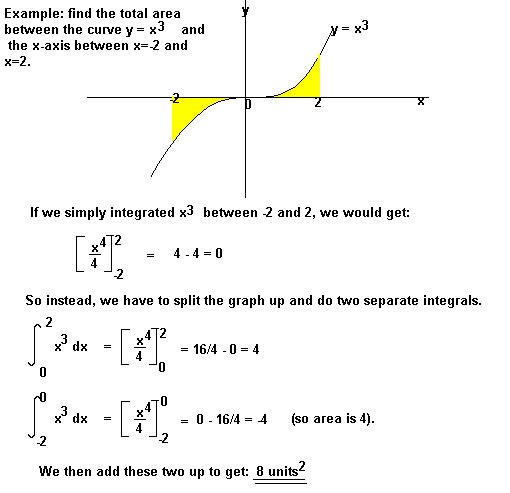
Du kan også blive bedt om at finde området mellem kurven og y-aksen. For at gøre dette skal du integrere med hensyn til y.
eksempel
Find det område, der er afgrænset af linjerne y = 0, y = 1 og y = .2.