Indledning
Lineær regression, også kendt som simpel lineær regression eller bivariate lineær regression, bruges, når vi ønsker at forudsige værdien af en afhængig variabel, der er baseret på værdien af en uafhængig variabel. For eksempel kan du bruge lineær regression til at forstå, om eksamensydelse kan forudsiges baseret på revisionstid (dvs.,, din afhængige variabel ville være” eksamensydelse”, målt fra 0-100 mærker, og din uafhængige variabel ville være” revisionstid”, målt i timer). Skiftevis, du kan bruge lineær regression til at forstå, om forbruget af cigaretter, kan forudsiges baseret på værelser varighed (dvs, din afhængige variabel ville være “cigaret forbrug”, målt i forhold til antallet af cigaretter, der indtages dagligt, og din uafhængige variabel ville være “ryger varighed”, målt i dage). Hvis du har to eller flere uafhængige variabler, snarere end blot en, skal du bruge flere regression., Alternativt, hvis du bare ønsker at fastslå, om der findes et lineært forhold, kan du bruge Pearsons korrelation.
Bemærk: den afhængige variabel kaldes også resultat -, mål-eller kriterievariablen, mens den uafhængige variabel også kaldes Forudsigelses -, forklarende eller regressorvariablen. I sidste ende, uanset hvilket udtryk du bruger, er det bedst at være konsekvent. Vi vil henvise til disse som afhængige og uafhængige variabler i hele denne vejledning.,
i denne vejledning viser vi dig, hvordan du udfører lineær regression ved hjælp af Stata, samt fortolker og rapporterer resultaterne fra denne test. Men før vi introducerer dig til denne procedure, skal du forstå de forskellige antagelser, som dine data skal opfylde for at lineær regression skal give dig et gyldigt resultat. Vi diskuterer disse antagelser næste.
Stata
antagelser
Der er syv “antagelser”, der understøtter lineær regression. Hvis nogen af disse syv antagelser ikke er opfyldt, kan du ikke analysere dine data ved hjælp af lineær, fordi du ikke får et gyldigt resultat., Da antagelser # 1 og # 2 vedrører dit valg af variabler, kan de ikke testes for at bruge Stata. Du skal dog beslutte, om din undersøgelse opfylder disse antagelser, før du går videre.1: din afhængige variabel skal måles på det kontinuerlige niveau., Eksempler på sådanne kontinuerlige variabler højde (målt i fod og tommer), temperatur (målt i oC), løn (målt i US-dollars), revision tiden (målt i timer), intelligens (målt ved hjælp af IQ-score), reaktionstid (målt i millisekunder), test resultater (målt fra 0 til 100), salg (målt i antal transaktioner per måned), og så videre. Hvis du er usikker på, om din afhængige variabel er kontinuerlig (dvs. målt på interval-eller forholdsniveau), se vores Variabelvejledning.,2: din uafhængige variabel skal måles på det kontinuerlige eller kategoriske niveau. Men hvis du har en kategorisk uafhængig variabel, er det mere almindeligt at bruge en uafhængig t-test (for 2 grupper) eller envejs ANOVA (for 3 grupper eller mere). I tilfælde af at du er usikker på, eksempler på kategoriske variabler som køn (fx, 2 grupper: mandlige og kvindelige), etnisk oprindelse (fx, 3 grupper: Hvide, sorte og Spansktalende), fysisk aktivitet (fx, 4 grupper: inaktive, lav, moderat og høj), og erhverv (fx,, 5 grupper: kirurg, Læge, Sygeplejerske, tandlæge, terapeut). I denne vejledning viser vi dig den lineære regressionsprocedure og Stata-output, når både dine afhængige og uafhængige variabler blev målt på et kontinuerligt niveau.
heldigvis kan du kontrollere antagelser #3, #4, #5, #6 og # 7 ved hjælp af Stata. Når man går videre til antagelser #3, #4, #5, #6 og # 7 foreslår vi at teste dem i denne rækkefølge, fordi det repræsenterer en ordre, hvor du ikke længere kan bruge lineær regression, hvis en overtrædelse af antagelsen ikke kan korrigeres., Faktisk skal du ikke blive overrasket, hvis dine data fejler en eller flere af disse antagelser, da dette er ret typisk, når du arbejder med data i den virkelige verden snarere end lærebogeksempler, som ofte kun viser dig, hvordan du udfører lineær regression, når alt går godt. Du skal dog ikke bekymre dig, for selv når dine data fejler visse antagelser, er der ofte en løsning til at overvinde dette (f.eks., Bare husk, at hvis du ikke kontrollerer, at dine data opfylder disse antagelser, eller du tester for dem forkert, er de resultater, du får, når du kører lineær regression, muligvis ikke gyldige.3: der skal være et lineært forhold mellem de afhængige og uafhængige variabler. Selvom der er en række måder at kontrollere, om der findes et lineært forhold mellem dine to variabler, foreslår vi at oprette en scatterplot ved hjælp af Stata, hvor du kan plotte den afhængige variabel mod din uafhængige variabel., Du kan derefter visuelt inspicere scatterplot at kontrollere for linearitet. Din scatterplot kan se noget som ét af følgende:
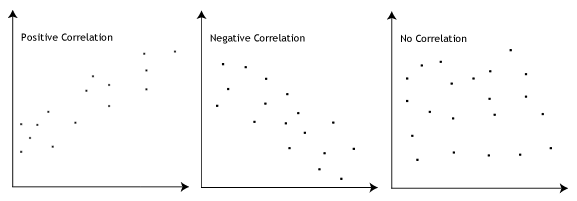
Hvis de forhold, der vises i din scatterplot ikke er lineær, vil du nødt til enten at køre en ikke-lineær regression, analyse eller “omdanne” dine data, som du kan gøre brug af Stata.4: der bør ikke være nogen signifikante outliers. Outliers er simpelthen enkelte datapunkter i dine data, der ikke følger det sædvanlige mønster (f. eks.,, i en undersøgelse af 100 studerendes i. – score, hvor den gennemsnitlige score var 108 med kun en lille variation mellem studerende, havde en studerende en score på 156, hvilket er meget usædvanligt, og kan endda sætte hende i top 1% af i. – score globalt). Følgende scatterplots fremhæve den potentielle indvirkning af outliers:
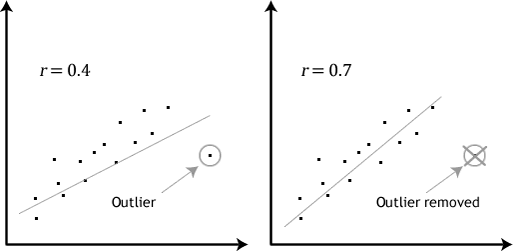
problemet med outliers er, at de kan have en negativ effekt på regressionsligningen, der bruges til at forudsige værdien af den afhængige variabel, der er baseret på den uafhængige variabel., Dette vil ændre output, som Stata producerer, og reducere forudsigelsesnøjagtigheden af dine resultater. Heldigvis kan du bruge Stata til at udføre case .ise diagnostik for at hjælpe dig med at opdage mulige outliers.5: Du skal have uafhængighed af observationer, som du nemt kan kontrollere ved hjælp af Durbin-.atson-statistikken, som er en simpel test, der skal køres ved hjælp af Stata.6: dine data skal vise homoscedasticitet, hvilket er hvor afvigelserne langs linjen med bedste pasform forbliver ens, når du bevæger dig langs linjen., De to scatterplots nedenfor give enkle eksempler på data, der opfylder denne antagelse, og én, der svigter den antagelse:
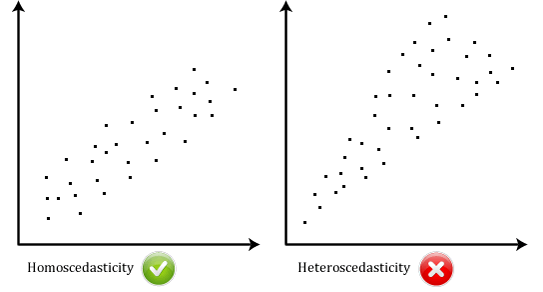
Når du analysere dine egne data, du vil være heldig, hvis dit scatterplot ser ud som en af de to ovenstående. Selvom disse hjælper med at illustrere forskellene i data, der opfylder eller krænker antagelsen om homoscedasticitet, er data i den virkelige verden ofte meget mere rodet., Du kan kontrollere, om dine data viste homoscedasticity ved at plotte regression standardiserede rester mod regression standardiseret forudsagt værdi.7: Endelig skal du kontrollere, at regressionslinjens rester (fejl) er omtrent normalt fordelt. To almindelige metoder til at kontrollere denne antagelse inkluderer anvendelse af enten et histogram (med en overlejret normal kurve) eller et normalt P-P-Plot.
i praksis, kontrol af antagelser #3, #4, #5, #6 og # 7 vil sandsynligvis tage det meste af din tid, når du udfører lineær regression., Det er dog ikke en vanskelig opgave, og Stata leverer alle de værktøjer, du har brug for for at gøre dette.
i afsnittet Procedure illustrerer vi Stata-proceduren, der kræves for at udføre lineær regression under forudsætning af, at ingen antagelser er blevet overtrådt. Først beskriver vi det eksempel, vi bruger til at forklare den lineære regressionsprocedure i Stata.
Stata
eksempel
undersøgelser viser, at træning kan hjælpe med at forhindre hjertesygdomme. Inden for rimelige grænser, jo mere du træner, jo mindre risiko har du for at lide af hjertesygdomme., En måde, hvorpå motion reducerer din risiko for at lide af hjertesygdomme, er ved at reducere et fedt i dit blod, kaldet kolesterol. Jo mere du træner, jo lavere er din kolesterolkoncentration. Det er desuden for nylig blevet vist, at den mængde tid, du bruger på at se FJERNSYN – en indikator for en stillesiddende livsstil – kan være en god prædiktor for hjertesygdom (dvs, der er, jo mere FJERNSYN du ser, jo større er din risiko for hjertesygdomme).,
derfor besluttede en forsker at afgøre, om kolesterolkoncentrationen var relateret til tid brugt på at se TV hos ellers sunde 45 Til 65 år gamle mænd (en risikokategori af mennesker). For eksempel, da folk brugte mere tid på at se TV, steg deres kolesterolkoncentration også (et positivt forhold); eller skete det modsatte? Forskeren ønskede også at kende andelen af kolesterolkoncentration, som den tid, der blev brugt på at se TV, kunne forklare, samt at være i stand til at forudsige kolesterolkoncentration., Forskeren kunne derefter afgøre, om for eksempel mennesker, der brugte otte timer på at se TV om dagen, havde farligt høje niveauer af kolesterolkoncentration sammenlignet med folk, der så kun to timers TV.
for at udføre analysen rekrutterede forskeren 100 sunde mandlige deltagere mellem 45 og 65 år. Mængden af tid brugt på at se TV (dvs, den uafhængige variabel, time_tv) og kolesterol koncentration (dvs, den afhængige variabel, kolesterol) blev registreret for alle 100 deltagere., Udtrykt i variable termer ønskede forskeren at regressere kolesterol på time_tv.
Bemærk: eksemplet og de data, der bruges til denne vejledning, er fiktive. Vi har netop oprettet dem med henblik på denne vejledning.
Stata
Opsætning i Stata
Bemærk: Det betyder ikke noget, om du først opretter den afhængige eller uafhængige variabel.
efter oprettelse af disse to variabler – time_tv og kolesterol-indtastede vi scoringerne for hver i de to kolonner i Dataeditoren (Rediger) regneark (dvs., den tid i timer, som deltagerne har set TV i den venstre kolonne, (dvs, time_tv, den uafhængige variabel), og deltagernes kolesterol koncentration i mmol/L i den højre kolonne (dvs, kolesterol, den afhængige variabel), som vist nedenfor:
Udgivet med skriftlig tilladelse fra StataCorp LP.,
Stata
Test Procedure i Stata
I dette afsnit viser vi dig, hvordan til at analysere dine data ved hjælp af en lineær regression Stata, når de seks antagelser i det foregående afsnit, Antagelser, ikke er blevet krænket. Du kan udføre lineær regression ved hjælp af kode eller statas grafiske brugergrænseflade (GUI). Når du har udført din analyse, viser vi dig, hvordan du fortolker dine resultater. Vælg først, om du vil bruge kode eller statas grafiske brugergrænseflade (GUI).,
– Kode
koden til at foretage lineær regression på dine data tager form:
relatere DependentVariable IndependentVariable
Denne kode er indtastet i boksen nedenfor:
Udgivet med skriftlig tilladelse fra StataCorp LP.,
ved Hjælp af vores eksempel, hvor den afhængige variabel er kolesterol og den uafhængige variabel er time_tv, den nødvendige kode ville være:
relatere kolesterol time_tv
Bemærk 1: Du er nødt til at være præcis, når du indtaster koden i max. Koden er “store og små bogstaver”. For eksempel, hvis du har indtastet “kolesterol”, hvor ” C ” er store bogstaver i stedet for små bogstaver (dvs ., et lille “c”), som det skal være, vil du få en fejlmeddelelse som følgende:
Bemærk 2: Hvis du stadig får en fejlmeddelelse i Note 2: ovenstående, det er værd at kontrollere det navn, du gav din to variabler i Data-Editoren, når du opretter din fil (dvs, se de Data Editor-skærmbilledet ovenfor)., I boksen i højre side af Dataredigeringsskærmen er det den måde, du stavede dine variabler i afsnittet
, ikke afsnittet
, som du skal indtaste koden (se nedenfor for vores afhængige variabel). Dette kan virke indlysende, men det er en fejl, der undertiden laves, hvilket resulterer i fejlen i Note 2 ovenfor.
indtast derfor koden, regress cholesterol time_tv, og tryk på knappen “Return/Enter” på dit tastatur.,
Udgivet med skriftlig tilladelse fra StataCorp LP.
Du kan se Stata output, der vil blive produceret her.,
Graphical User Interface (GUI)
De tre trin, der kræves for at udføre lineær regression Stata 12 og 13 er vist nedenfor:
- Klik på Statistik > Lineære modeller og relaterede > Lineær regression på hovedmenuen, som vist nedenfor:
Udgivet med skriftlig tilladelse fra StataCorp LP.,
Du vil blive præsenteret med Tilbagegang – Lineær regression dialog boks:
Udgivet med skriftlig tilladelse fra StataCorp LP.
- Vælg kolesterol fra inden for den Afhængige variabel: drop-down boks, og time_tv fra de Uafhængige variable: drop-down boks. Du vil ende op med følgende skærmbillede:
Udgivet med skriftlig tilladelse fra StataCorp LP.,
-
Klik på
knappen. Dette vil generere output.
Stata
Output af lineær regressionsanalyse i Stata
Hvis dine data er gået antagelse #3 (dvs, der var en lineær sammenhæng mellem to variabler), #4 (dvs, der var ingen signifikant afvigende værdier), antagelse #5 (dvs, du havde uafhængighed af observationer), antagelse, #6 (dvs, dine data viste homoscedasticity) og antagelse af #7 (dvs, den residualer (fejl) var ca normalfordelt), som vi forklarede tidligere i de Forudsætninger afdeling, vil du kun nødt til at fortolke de følgende lineære regression output i Stata:
Udgivet med skriftlig tilladelse fra StataCorp LP.,
output består af fire vigtige oplysninger: (a) R2-værdi (“R-squared” row) repræsenterer den del af variansen i den afhængige variabel, der kan forklares af vores uafhængige variabel (teknisk set er det den andel af variationen forklares ved, at der regressionsmodel, som ligger ud over den gennemsnitlige model). Imidlertid er R2 baseret på prøven og er et positivt forudindtaget skøn over andelen af variansen af den afhængige variabel, der er tegnede sig for regressionsmodellen (dvs ., det er for stort); (b) et justeret R2-værdi (“Adj R-squared” row), som korrigerer positiv bias for at give en værdi, som ville kunne forventes i befolkningen; (c) F-værdi, grader af frihed (“F( 1, 98)”), og den statistiske signifikans af regression model (“Prob > F” row); og (d) koefficienterne for den konstante og uafhængige variable (“Coef.”kolonne), som er de oplysninger, du har brug for at forudsige den afhængige variabel, kolesterol, ved hjælp af den uafhængige variabel, time_tv.
i dette eksempel, R2 = 0,151. Justeret R2 = 0,143 (til 3 d. P.,), hvilket betyder, at den uafhængige variabel, time_tv, forklarer 14, 3% af variabiliteten af den afhængige variabel, kolesterol, i befolkningen. Justeret R2 er også et estimat af effektstørrelsen, som ved 0.143 (14.3%) er indikativ for en medium effektstørrelse ifølge Cohens (1988) klassificering. Men normalt er det R2 ikke den justerede R2, der er rapporteret i resultater. I dette eksempel er regressionsmodellen statistisk signifikant, F (1, 98) = 17, 47, p = .0001., Dette indikerer, at den anvendte model generelt kan statistisk signifikant forudsige den afhængige variabel, kolesterol.
Bemærk: Vi præsenterer output fra den lineære regressionsanalyse ovenfor. Da du imidlertid skulle have testet dine data for de antagelser, vi forklarede tidligere i afsnittet antagelser, skal du også fortolke Stata-output, der blev produceret, da du testede for disse antagelser. Dette inkluderer: (a) de scatterplots, du brugte til at kontrollere, om der var et lineært forhold mellem dine to variabler (dvs .,, Antagelse #3); (b) casewise diagnose at undersøge, om der var ingen signifikant afvigende værdier (dvs, Antagelse #4); (c) output fra Durbin-Watson statistik ind til uafhængighed af observationer (dvs, Antagelse #5); (d) et scatterplot af regression standardiserede residualer mod de regression standardized predicted value at afgøre, om dine data viste homoscedasticity (dvs, Antagelse #6); og et histogram (med overlejret normale kurve) og Normal P-P Plot for at kontrollere, om residualer (fejl) var ca normalt fordelt (dvs, Antagelse #7)., Husk også, at hvis dine data mislykkedes nogen af disse antagelser, vil det output, du får fra den lineære regressionsprocedure (dvs.det output, vi diskuterer ovenfor), ikke længere være relevant, og du skal muligvis udføre en anden statistisk test for at analysere dine data.,
Stata
Rapportering produktionen af lineær regressionsanalyse
Når du rapporterer resultatet af en lineær regression, er det god praksis at omfatte: (a) en introduktion til den analyse, du gennemføres; (b) oplysninger om din prøve, herunder eventuelle manglende værdier; (c) den observerede F-værdi, grader af frihed og betydning (dvs, p-værdi); (d) den procentdel af variationen i den afhængige variabel forklares af de uafhængige variable (dvs, din Justeret R2 ); og (e) regressionsligningen for din model., Baseret på ovenstående resultater, vi kunne rapport om resultaterne af denne undersøgelse som følger:
- Generelt
En lineær regression, der er etableret, at den daglige tid brugt på at se TV kunne statistisk signifikant forudsige kolesterol koncentration, F(1, 98) = 17.47, p = .0001 og tid brugt på at se TV tegnede sig for 14,3% af den forklarede variabilitet i kolesterolkoncentration. Regressionsligningen var: forudsagt kolesterolkoncentration = -2.135 + 0.044. (tid brugt på at se tv).,
ud over at rapportere resultaterne som ovenfor, kan et diagram bruges til visuelt at præsentere dine resultater. For eksempel kan du gøre dette ved hjælp af en scatterplot med tillid og forudsigelsesintervaller (selvom det ikke er meget almindeligt at tilføje det sidste). Dette kan gøre det lettere for andre at forstå dine resultater. Desuden kan du bruge din lineære regressionsligning til at lave forudsigelser om værdien af den afhængige variabel baseret på forskellige værdier af den uafhængige variabel., Mens Stata ikke producerer disse værdier som en del af den lineære regressionsprocedure ovenfor, er der en procedure i Stata, som du kan bruge til at gøre det.