Vi klassisk tænker på lys som altid rejser i lige linjer, men når lysbølger passerer nær en barriere, har de en tendens til at bøje sig omkring den barriere og blive spredt ud. Diffraktion af lys opstår, når en lysbølge passerer ved et hjørne eller gennem en åbning eller spalte, der er fysisk den omtrentlige størrelse af, eller endda mindre end lysets bølgelængde.,

en meget enkel demonstration af diffraktion kan udføres ved at holde hånden foran en lyskilde og langsomt lukke to fingre, mens man observerer det lys, der transmitteres mellem dem. Når fingrene nærmer sig hinanden og kommer meget tæt sammen, begynder du at se en række mørke linjer parallelt med fingrene. De parallelle linjer er faktisk diffraktionsmønstre. Dette fænomen kan også forekomme, når lyset er “bøjet” omkring partikler, der er i samme størrelsesorden som lysets bølgelængde., Et godt eksempel på dette er diffraktionen af sollys af skyer, som vi ofte omtaler som et sølvfor, illustreret i Figur 1 med en smuk solnedgang over havet.
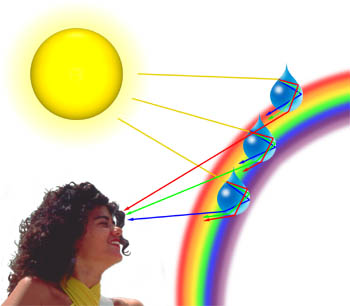
Vi kan ofte observere pastelfarver af blå, lyserød, lilla og grøn i skyer, der genereres, når lys diffraheres fra vanddråber i skyerne. Mængden af diffraktion afhænger af bølgelængden af lyset, med kortere bølgelængder er diffracted i en større vinkel, end længere dem (i kraft, blå og violet lys er diffracted i en højere vinkel end det, der er rødt lys)., Når en lysbølge, der rejser gennem atmosfæren, støder på en dråbe vand, som illustreret nedenfor, brydes den først ved waterater:air-grænsefladen, så afspejles den, når den igen møder grænsefladen. Strålen, der stadig rejser inde i vanddråben, brydes igen, da den rammer grænsefladen for tredje gang. Denne sidste interaktion med grænsefladen bryder lyset tilbage i atmosfæren, men det diffracerer også en del af lyset som illustreret nedenfor., Dette diffraktionselement fører til et fænomen kendt som Cellinis halo (også kendt som Heiligenschein-effekten), hvor en lys ring af lys omgiver skyggen af observatørens hoved.
udtrykkene diffraktion og spredning bruges ofte om hverandre og betragtes som næsten synonyme. Diffraktion beskriver et specialiseret tilfælde af lysspredning, hvor et objekt med regelmæssigt gentagne funktioner (såsom et diffraktionsgitter) frembringer en ordnet diffraktion af lys i et diffraktionsmønster., I den virkelige verden er de fleste objekter meget komplekse i form og bør betragtes som sammensat af mange individuelle diffraktionsfunktioner, der samlet kan producere en tilfældig spredning af lys.
et af de klassiske og mest grundlæggende begreber, der involverer diffraktion, er det optiske diffraktionseksperiment med enkelt spalte, der først blev udført i begyndelsen af det nittende århundrede. Når en lysbølge udbreder sig gennem en spalte (eller blænde), afhænger resultatet af den fysiske størrelse af blænden med hensyn til bølgelængden af den indfaldende stråle., Dette er illustreret i Figur 3 antages en sammenhængende, monokromatiske bølge udsendt fra punktet kilden S, svarende til lys, der ville blive produceret af en laser, passerer gennem blænde d og er diffracted, med det primære indfaldende lys stråle, der lander i punktet P og den første afledte maxima, der forekommer i punkt Q.
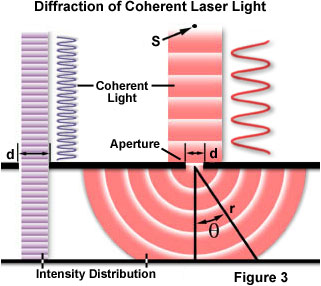
Som vist i venstre side af figuren, når bølgelængden (λ) er meget mindre end åbningens bredde (d), den bølge blot bevæger sig fremad i en lige linje, lige som det ville, hvis det var en partikel eller ikke blænde var til stede., Men når den bølgelængde, der overstiger størrelsen af den åbning, vi oplever diffraktion for lys i henhold til ligningen:
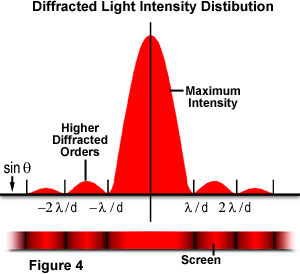
Hvor θ er vinklen mellem hændelsen centrale formering retning, og den første minimum af diffraktion mønster. Eksperimentet producerer et lyst centralt maksimum, der flankeres på begge sider af sekundære maksimum, med intensiteten af hvert efterfølgende sekundært maksimum falder, når afstanden fra midten øges. Figur 4 illustrerer dette punkt med et plot af stråle intensitet versus diffraktionsradius., Bemærk, at de minima, der forekommer mellem sekundære maksima, er placeret i multipla af π.
dette eksperiment blev først forklaret af Augustin Fresnel, der sammen med Thomas Young producerede vigtige beviser, der bekræfter, at lyset rejser i bølger. Fra ovenstående figurer ser vi, hvordan et sammenhængende, monokromatisk lys (i dette eksempel laserbelysning) udsendt fra punkt L diffraheres ved blænde d., Fresnel antages, at amplituden af den første ordre maksima i punkt Q (defineret som eQ) vil være givet ved ligningen:
hvor A er amplituden af den indfaldende bølge, r er afstanden mellem d og Q, og f(χ) er en funktion χ, en tilbøjelighed faktor indført af Fresnel.
diffraktion af lys
Udforsk, hvordan en lysstråle diffraheres, når den passerer gennem en smal spalte eller åbning. Juster bølgelængde og Blænde størrelse og observere, hvordan dette påvirker diffraktion intensitet mønster.,
diffraktion af lys spiller en vigtig rolle i begrænsningen af opløsningskraften for ethvert optisk instrument (for eksempel: kameraer, kikkert, teleskoper, mikroskoper og øjet). Løsningskraften er det optiske Instruments evne til at producere separate billeder af to tilstødende punkter. Dette bestemmes ofte af kvaliteten af linser og spejle i instrumentet samt egenskaberne af det omgivende medium (normalt luft). Lysets bølgelignende natur tvinger en ultimativ grænse for opløsningskraften for alle optiske instrumenter.,
vores diskussioner om diffraktion har brugt en spalte som blænden, gennem hvilken lys diffrakteres. Imidlertid har alle optiske instrumenter cirkulære åbninger, for eksempel pupillen i et øje eller den cirkulære membran og linser i et mikroskop. Cirkulære åbninger frembringer diffraktionsmønstre svarende til dem, der er beskrevet ovenfor, bortset fra at mønsteret naturligt udviser en cirkulær symmetri. Matematisk analyse af diffraktionsmønstrene produceret af en cirkulær blænde er beskrevet ved ligningen:
hvor θ(1) er den vinkel position i den første ordre, diffraktion minima (den første mørke ring), λ er bølgelængden af det indfaldende lys, d er diameteren af åbningen, og 1.22 er en konstant. Under de fleste omstændigheder, vinklen θ(1) er meget lille, så den tilnærmelse, at synden og tan af den vinkel er næsten lige udbytter:
Fra disse ligninger bliver det tydeligt, at den centrale maksimale, er direkte proportional med λ/d for at gøre dette maksimale mere spredt ud til længere bølgelængder, og for mindre åbninger., Den sekundære Mimina af diffraktion sætter en grænse for den nyttige forstørrelse af objektive linser i optisk mikroskopi på grund af iboende diffraktion af lys ved disse linser. Uanset hvor perfekt linsen kan være, er billedet af en punktkilde af lys produceret af linsen ledsaget af sekundære og højere orden Maksima. Dette kunne kun fjernes, hvis linsen havde en uendelig diameter. To objekter adskilt af en afstand mindre end θ (1) kan ikke løses, uanset hvor høj forstørrelseseffekten er., Mens disse ligninger blev afledt for billedet af en punktkilde af lys en uendelig afstand fra åbningen, er det en rimelig tilnærmelse af løsningen magt et mikroskop, når d er erstattet af diameteren af objektivlinsen.
så hvis to objekter bor en afstand d fra hinanden og er i en afstand L fra en observatør, er vinklen (udtrykt i radianer) mellem dem:
hvilket fører os til at kunne kondensere de sidste to ligninger til udbytte:
hvor D (0) er den mindste adskillelsesafstand mellem de objekter, der gør det muligt at løse dem. Ved hjælp af denne ligning, er det menneskelige øje kan løse objekter, der er adskilt af en afstand af 0.056 millimeter, men de fotoreceptorer i retina er ikke helt tæt nok sammen til at tillade, at denne grad af opløsning, og 0,1 millimeter er et mere realistisk tal under normale omstændigheder.
opløsningskraften af optiske mikroskoper bestemmes af en række faktorer, herunder de diskuterede, men under de mest ideelle omstændigheder er dette tal omkring 0,2 mikrometer., Dette tal skal tage højde for optisk justering af mikroskopet, linsernes kvalitet samt de overvejende bølgelængder af lys, der bruges til at afbilde prøven. Mens det ofte ikke nødvendigt at beregne nøjagtige opløsningsevne af hvert enkelt mål (og ville være spild af tid, i de fleste tilfælde), er det vigtigt at forstå mulighederne i mikroskop linser, som de gælder for den virkelige verden.
bidragende forfattere
Mortimer Abramo .it. – Olympus America, Inc., To Corporate Center Drev., Melville, Ne Mel York, 11747.Michael W.., Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.