Læringsresultater
- Identificere poler, vertices, økser, og centrum af en ellipse.
- skriv ligninger af ellipser centreret ved oprindelsen.
- skriv ligninger af ellipser, der ikke er centreret ved oprindelsen.
en konisk sektion eller konisk er en form, der skyldes krydsning af en højre cirkulær kegle med et plan. Den vinkel, hvor planet skærer keglen, bestemmer formen.,
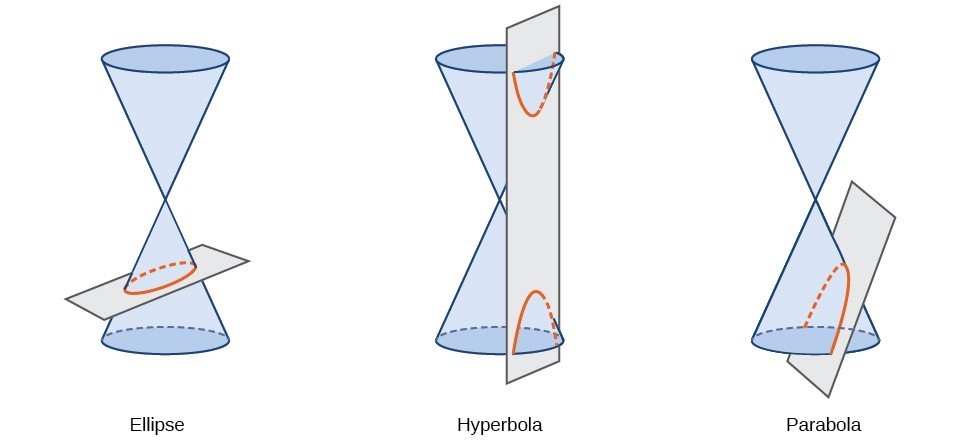
koniske sektioner kan også beskrives ved et sæt punkter i koordinatplanet. Senere i dette kapitel vil vi se, at grafen af enhver kvadratisk ligning i to variabler er en conic sektion. Tegnene på ligningerne og koefficienterne for de variable udtryk bestemmer formen. Dette afsnit fokuserer på de fire variationer af standardformen af ligningen for ellipsen. En ellipse er sæt af alle punkter \venstre (y, y \ højre) i et plan, således at summen af deres afstande fra to faste punkter er en konstant., Hvert fast punkt kaldes et fokus (flertal: foci) af ellipsen.
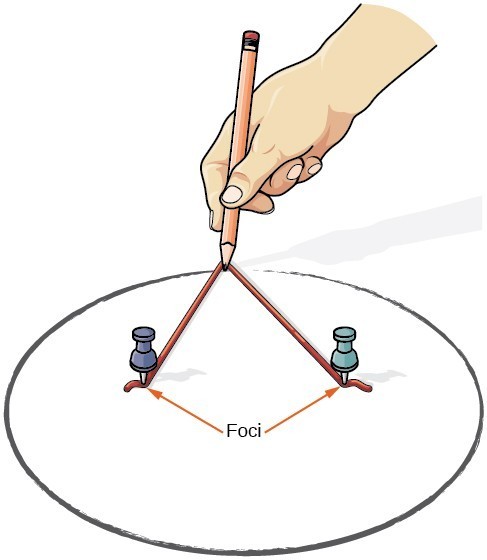
Vi kan tegne en ellipse ved hjælp af et stykke pap, to tommelfingre, en blyant og streng. Placer tommelfingeren i papen for at danne ellipsens foci. Klip et stykke snor længere end afstanden mellem de to tommelfingre (længden af strengen repræsenterer konstanten i definitionen). Tack hver ende af strengen til pap, og spore en kurve med en blyant holdt stramt mod strengen. Resultatet er en ellipse.
hver ellipse har to symmetriakser., Den længere akse kaldes hovedaksen, og den kortere akse kaldes den mindre akse. Hver endepunkt af den store akse er toppunktet af ellipsen (flertal: knudepunkter), og hvert endepunkt af den mindre akse er en co-toppunkt af ellipsen. Midten af en ellipse er midtpunktet af både de store og mindre akser. Akserne er vinkelret i midten. Foci ligger altid på hovedaksen, og summen af afstande fra foci til ethvert punkt på ellipsen (den konstante sum) er større end afstanden mellem foci.,
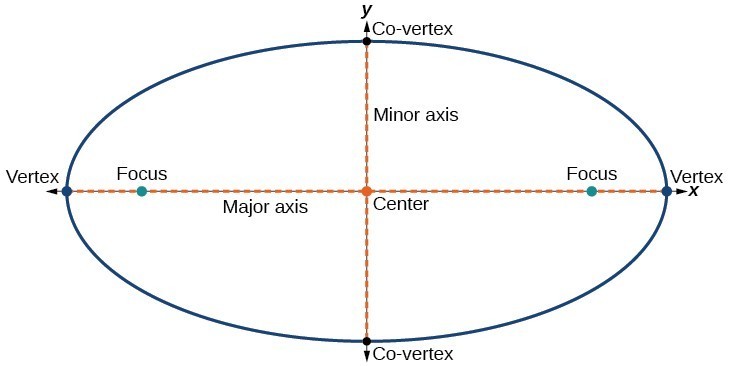
I dette afsnit vil vi begrænse ellipser til dem, der er placeret lodret eller vandret i koordinatplanen. Det vil sige, akserne vil enten ligge på eller være parallelle med axes– og y-akserne. Senere i kapitlet vil vi se ellipser, der roteres i koordinatplanet.
for at arbejde med vandrette og lodrette ellipser i koordinatplanet overvejer vi to tilfælde: dem, der er centreret ved oprindelsen, og dem, der er centreret på et andet punkt end oprindelsen., Først lærer vi at udlede ellipsernes ligninger, og så lærer vi at skrive ellipsernes ligninger i standardform. Senere vil vi bruge det, vi lærer at tegne graferne.,v>If (x,y) er et punkt på ellipsen, så kan vi definere følgende variabler:
\begin{align}d_1&=\text{afstanden fra } (-k,0) \text{ for at } (x,y) \\ d_2&= \text{afstanden fra } (c,0) \text{ for at } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
for en ellipse, der er centreret på den oprindelse med dens hovedakse, som på X-aksen og
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
for en ellipse, der er centreret på den oprindelse med sin store akse om Y-aksen.,
du Skriver Ligninger af Ellipser Ikke Centreret på Oprindelsen
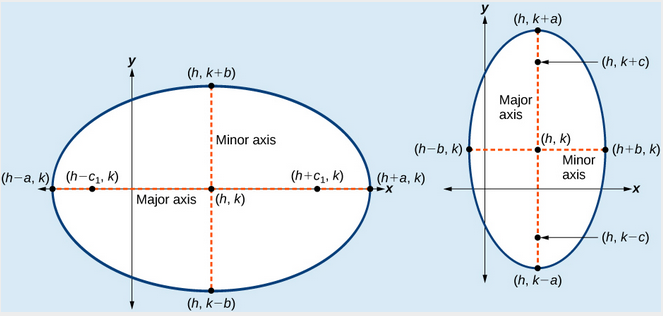
(a) Vandret ellipse med centrum i \left(h,k\right) (b) Lodret ellipse med centrum i \left(h,k\right)
Løsning Anvendes Problemer med Ellipser
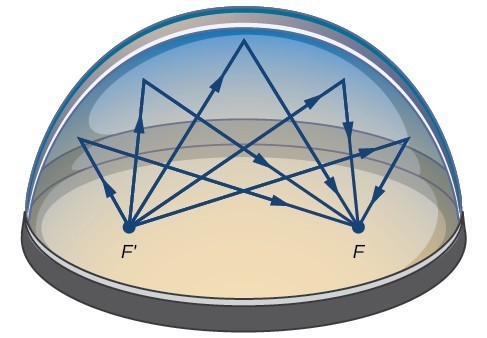
Mange virkelige verden situationer, kan være repræsenteret ved ellipser, herunder baner af planeter, satellitter, måner og kometer, og figurer af båd køl, ror, og nogle af flyvinger. En medicinsk anordning kaldet en lithotripter bruger elliptiske reflektorer til at bryde op nyresten ved at generere lydbølger., Nogle bygninger, kaldet hviskekamre, er designet med elliptiske kupler, så en person, der hvisker ved et fokus, let kan høres af nogen, der står ved det andet fokus. Dette sker på grund af ellipsens akustiske egenskaber. Når en lydbølge stammer fra et fokus i et hviskekammer, vil lydbølgen blive reflekteret fra den elliptiske kuppel og tilbage til det andet fokus. I whisperhisper chamber på Museum of Science and Industry i Chicago, to mennesker, der står ved foci—omkring 43 fødder fra hinanden—kan høre hinanden hviske.