Dette er den første i en tre indlæg serie. Det andet indlæg taler om hvordan man beregner Big-O. Den tredje artikel taler om forståelseden formelle definition af Big-O.
Big-O notation plejede at være et virkelig skræmmende koncept for mig. Jeg troede det er sådan, hvordan “rigtige” programmører talte om deres kode. Det var alt sammen mere skræmmende, fordi de akademiske beskrivelser (som Wikipedia) gav mig meget lidt mening. Dette er frustrerende, fordi de underliggende begreber ikke er så hårde.,kort sagt, Big-O notation er, hvordan programmører taler omalgoritmer. Algoritmer er et andet skræmmende emne, som jeg vil dække iet andet indlæg, men til vores formål, lad os sige, at “algoritme” betyder enfunktion i dit program (som ikke er for langt væk). En funktions Big-Onotation bestemmes af, hvordan den reagerer på forskellige input. Hvordanmeget langsommere er det, hvis vi giver det en liste over 1000 ting at arbejde påi stedet for en liste over 1 ting?
Overvej denne kode:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Så hvis vi kalder denne funktion som item_in_list(2, ), det shouldbe temmelig hurtig., Vi løber over hver ting på listen, og hvis vi finderdet første argument til vores funktion, returner True. Hvis vi kommer til slutog vi fandt det ikke, returnere falsk.
“kompleksiteten” af denne funktion er O(n). Jeg vil forklare, hvad dettebetyder om et sekund, men lad os nedbryde denne matematiske syntaks. O(n) læses” rækkefølge af N”, fordi funktionen O også er kendt som Ordrefunktionen. Jeg tror, det er fordi vi gørapproximimation, som handler i “størrelsesordener”.,
“størrelsesordener” er endnu et matematisk udtryk somdybest set fortæller forskellen mellem klasser af tal. Tænk på forskellen mellem 10 og 100. Hvis du forestiller dig 10 af dine tættevenner og 100 mennesker, er det en rigtig stor forskel. Tilsvarende er forskellen mellem 1.000 og 10.000 ret stor (faktisk er den forskellen mellem en junker bil og en let brugt). Det viser sigat i tilnærmelse, så længe du er inden for en størrelsesorden,er du temmelig tæt., Hvis du skulle gætte antallet af gumballs i amachine, ville du være inden for en størrelsesorden, hvis du sagde 200gumballs. 10.000 gumballs ville være langt væk.

Figur 1: en gumball-maskine, hvis antal gumballs sandsynligvis ligger inden for en størrelsesorden på 200.
Tilbage til at dissekere O(n), dette siger, at hvis vi skulle graf timeit tager at køre denne funktion med forskellige størrelse indgange (fx anarray af punkt 1, 2 elementer, 3 elementer, osv.), ville vi se, at itapproximately svarer til antallet af elementer i arrayet., Dette kaldes en lineær graf. Dette betyder, at linjen stort set er lige, hvis du skulle tegne den.
nogle af jer har måske fanget, at hvis ouritem i kodeprøven ovenfor altid var det første punkt på listen, ville vores kode være rigtig hurtig! Dette er sandt, men Big-O handler om den omtrentlige værste sagudførelse af at gøre noget. Det værste tilfælde for koden ovenfor er, at det, vi søger efter, slet ikke er på listen. (Bemærk:matematikbetegnelsen for dette er “øvre grænse”, hvilket betyder, at det taler om den matematiske grænse for a .fulness).,
Hvis du ønskede at se en graf for disse funktioner, ignorerer du funktionen O()og ændrer variablen nfor x. Du kan derefter skrive detinto Alphaolfram Alpha som “plot.”, som vil vise dig en diagonallinsk. Årsagen til at du bytter ud n for.er, at deres grafikprogramønsker x som dets variabelnavn, fordi det svarer til XA .is. X-aksen bliver større fra venstre mod højre svarer tilgive større og større arrays til din funktion., Y-aksenrepræsenterer tid, så jo højere linjen er, jo langsommere er den.
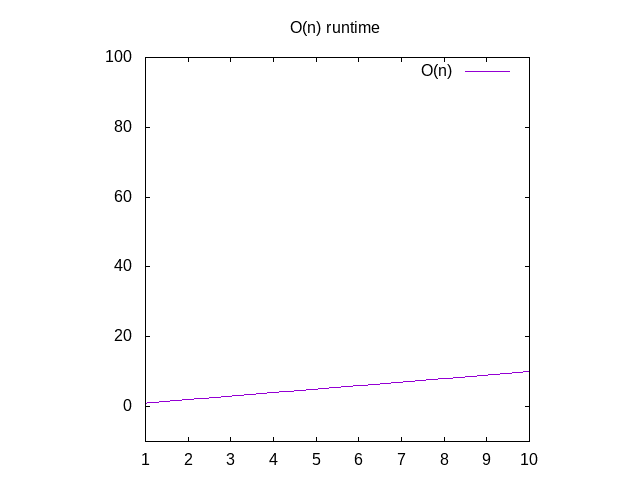
Figur 2: Runtime kendetegn for en O(n) funktion
Så hvad er nogle andre eksempler på dette?
overvej denne funktion:
def is_none(item): return item is None
Dette er lidt af et fjollet eksempel, men bær over med mig. Denne funktion erkaldet O(1) som kaldes “konstant tid”. Hvad dette betyder er nomatter hvor stor vores input er, det tager altid den samme tid at beregne ting., Hvis du går tilbage til diolfram og plot 1, vil du Seat det altid forbliver det samme, uanset hvor langt til højre vi går. Hvis youpass i en liste over 1 million heltal, vil det tage omkring samme tidsom om du skulle passere i en liste over 1 heltal. Konstant tid betragtes som det bedste tilfælde for en funktion.
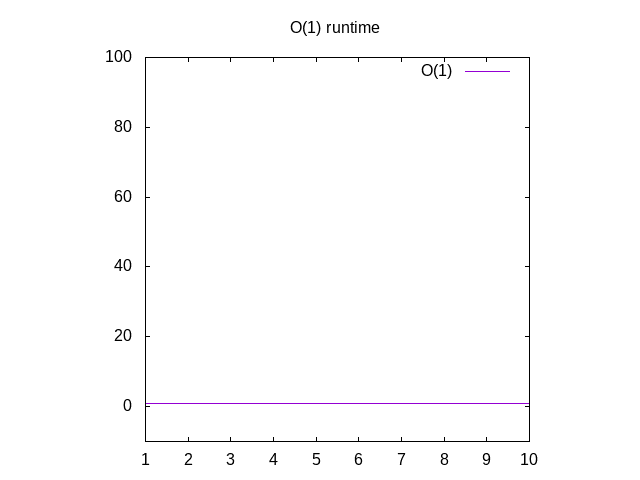
Figur 3: Runtime kendetegn for en O(1) funktion
Overvej denne funktion:
Nedenfor er en sammenligning af hver af disse grafer, til reference., Du kan se, at en O(n^2) funktion vil blive langsom meget hurtigt, hvor som noget, der fungerer i konstant tid, vil være meget bedre. Dette er især nyttigt, når det kommer til datastrukturer, som jeg vil skrive om snart.
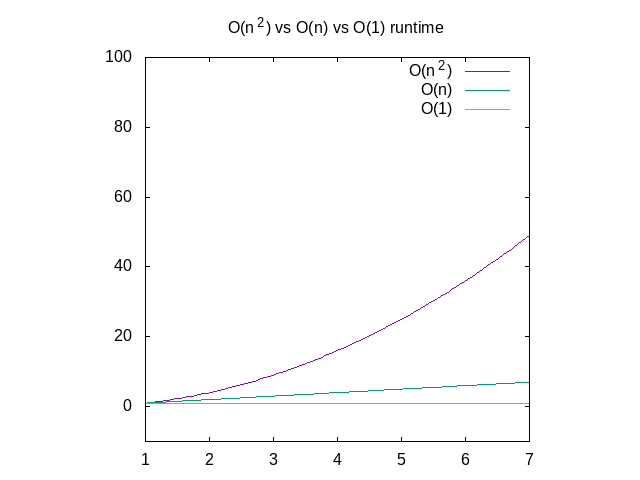
Figur 4: Sammenligning af O(n2) vs O(n) vs O(1) funktioner
Dette er et temmelig højt niveau overblik over Store-O-notation, men hopefullygets du bekendtskab med emnet., Der er et coursera kursus, som kan give dig et mere dybtgående indblik i dette emne, men vær advaret om, at det vil hoppe ind i matematisk notation meget hurtigt. Hvis noget her ikke giver mening, send mig en mail.
opdatering: Jeg har også skrevet om, hvordan man beregner Big-O.
Jeg tænker på at skrive en bog om dette emne. Hvis dette er noget, du gerne vil se, vær venlig at udtrykke din interesse for det her.