Modstande vs. Spoler
Spoler opfører sig ikke på samme måde som modstande gøre. Mens modstande simpelthen modsætter sig strømmen af strøm gennem dem (ved at droppe en spænding, der er direkte proportional med strømmen), induktorer modsætter sig ændringer i strøm gennem dem ved at droppe en spænding, der er direkte proportional med strømændringshastigheden.
i overensstemmelse med Len. ‘ s Lov er denne inducerede spænding altid af en sådan polaritet, at den forsøger at opretholde strøm til dens nutidsværdi., Det vil sige, hvis strømmen stiger i størrelse, vil den inducerede spænding “skubbe mod” strømstrømmen; hvis strømmen falder, vil polariteten vende og “skubbe med” strømmen for at modsætte sig faldet.
denne modstand mod den aktuelle ændring kaldes reaktans snarere end modstand., Udtrykt matematisk, forholdet mellem spænding faldt over den, spole og sats af aktuelle forandringer gennem induktoren, sådan som det er:

Vekselstrøm i en Simpel Induktive Kredsløb
udtrykket di/dt er en fra calculus, hvilket betyder, at graden af ændring af beregningen af det aktuelle (jeg) over tid, i ampere per sekund.
induktansen (L) er i Henrys, og den øjeblikkelige spænding (e) er selvfølgelig i volt., Nogle gange finder du hastigheden af øjeblikkelig spænding udtrykt som “v” i stedet for “e” (v = l di/dt), men det betyder nøjagtigt den samme ting.
for At vise, hvad der sker med vekselstrøm, lad os analysere en simpel spole kredsløb:
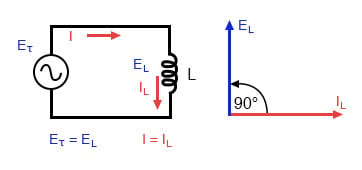
Rene induktive kredsløb: Spole aktuelle lag ‘ spole spænding ved 90°.
Hvis vi skulle plotte strømmen og spændingen for dette meget enkle kredsløb, ville det se sådan ud:

rent induktivt kredsløb, bølgeformer.,
Husk, at spændingen faldt over en induktor er en reaktion mod ændringen i strømmen gennem den.
Derfor, den øjeblikkelige spænding er nul, når den øjeblikkelige nuværende er på et højdepunkt (nul ændre eller niveau, hældning, på nuværende sinusbølge), og den øjeblikkelige spænding er på et højdepunkt, hvor den øjeblikkelige nuværende er på maksimal ændring (point af stejleste hældning på nuværende bølge, hvor den krydser nul linje).
dette resulterer i en spændingsbølge, der er 90 out ude af fase med den aktuelle bølge., Når man ser på grafen, ser spændingsbølgen ud til at have et “forspring” på den aktuelle bølge; spændingen “fører” strømmen og strømmen “hænger” bag spændingen.

strøm halter spænding ved 90.i et rent induktivt kredsløb.
ting bliver endnu mere interessante, når vi plotter strømmen til dette kredsløb:

i et rent induktivt kredsløb kan øjeblikkelig effekt være positiv eller negativ.,
da øjeblikkelig effekt er produktet af den øjeblikkelige spænding og den øjeblikkelige strøm (p=ie), er effekten lig med nul, når den øjeblikkelige strøm eller spænding er nul. Når den øjeblikkelige strøm og spænding begge er positive (over linjen), er strømmen positiv.
som med modstandseksemplet er effekten også positiv, når den øjeblikkelige strøm og spænding begge er negative (under linjen).,
Men, fordi de nuværende og spænding bølger er 90° ude af fase, der er tidspunkter, når man er positiv, mens den anden er negativ, hvilket resulterer i lige så hyppige forekomster af negative øjeblikkelig effekt.
Hvad er negativ effekt?
men hvad betyder negativ effekt? Det betyder, at induktoren frigiver strøm tilbage til kredsløbet, mens en positiv effekt betyder, at den absorberer strøm fra kredsløbet.,
da de positive og negative effektcyklusser er ens i størrelse og varighed over tid, frigiver induktoren lige så meget strøm tilbage til kredsløbet, som den absorberer i løbet af en komplet cyklus.
hvad dette betyder i praktisk forstand er, at reaktansen af en induktor spreder nettoenergi på nul, helt i modsætning til modstanden fra en modstand, der spreder energi i form af varme. Husk, dette er kun til perfekte induktorer, som ikke har nogen trådmodstand.
reaktans vs., Modstand
en induktors modstand mod ændring i strøm oversætter til en modstand mod vekselstrøm generelt, som per definition altid ændrer sig i øjeblikkelig størrelse og retning.
denne modstand mod vekselstrøm ligner modstand, men forskellig, idet den altid resulterer i et faseskift mellem strøm og spænding, og det spreder nul effekt. På grund af forskellene har den et andet navn: reaktans. Reaktans til AC udtrykkes i ohm, ligesom modstand er, bortset fra at dets matematiske symbol er R. I stedet for R.,
At være specifik, reaktans, der er forbundet med en spole er normalt symboliseret ved bogstavet X med et brev L som en sænket, ligesom dette: XL.
Da spoler drop spænding i forhold til den sats, der for nuværende ændre, vil de falde mere spænding for hurtigere skiftende strømme, og mindre spænding for langsommere skiftende strømninger. Hvad dette betyder er, at reaktans i ohm for enhver induktor er direkte proportional med frekvensen af vekselstrømmen., Den nøjagtige formel til at bestemme reaktans er som følger:

Hvis vi udsætter 10 mH induktor for frekvenser, 60, 120, og 2500 Hz, vil det manifestere den reactances i tabellen nedenfor.
Reaktans af en 10 mH spole:
| Frekvens (Hertz) | Reaktans (Ohm) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
I det reaktans ligning, udtrykket “2nf” (alt på højre side, undtagen L) har en særlig betydning i sig selv. Det er antallet af radianer per sekund, at vekselstrømmen er” roterende ” på, hvis du forestiller dig en cyklus af AC til at repræsentere en fuld cirkel rotation.
en radian er en enhed med vinkelmåling: der er 2 radi radianer i en fuld cirkel, ligesom der er 360.i en fuld cirkel., Hvis generatoren producerer AC er en dobbelt-polet enhed, vil det producere en cyklus for hver fuld drejning af akslen rotation, som er hver 2.radianer, eller 360..
hvis denne konstant på 2.ganges med frekvens i Hert. (cyklusser per sekund), vil resultatet være et tal i radianer per sekund, kendt som vinkelhastigheden af AC-systemet.
vinkelhastighed i AC-Systemer
vinkelhastighed kan være repræsenteret ved udtrykket 2nf, eller det kan blive repræsenteret af sin egen symbol, det lille græske bogstav omega, som vises ligner vores Romerske lavere-case “w”: ω., Reaktansformlen =l = 2nfL kunne således også skrives som .l = .l.
det skal forstås, at denne “vinkelhastighed” er et udtryk for, hvor hurtigt AC bølgeformer er cykling, en fuld-cyklus er lig med 2.radianer. Det er ikke nødvendigvis repræsentativt for den faktiske akselhastighed for generatoren, der producerer vekselstrømmen.hvis generatoren har mere end to poler, vil vinkelhastigheden være et multiplum af akselhastigheden., Af denne grund udtrykkes sometimes undertiden i enheder af elektriske radianer per sekund snarere end (almindelige) radianer per sekund for at skelne det fra mekanisk bevægelse.
på nogen måde udtrykker vi vinkelhastigheden af systemet, er det tydeligt, at det er direkte proportional med reaktans i en induktor. Da frekvensen (eller generatorakselhastigheden) øges i et vekselstrømssystem, vil en induktor give større modstand mod strømmen og omvendt.,
Vekselstrøm i en simpel induktive kredsløb er lig med spændingen (i volt), divideret med den induktive reaktans (i ohm), lige som enten vekselstrøm eller jævnstrøm i en simpel resistive kredsløb er lig med spændingen (i volt) divideret med modstand (i ohm). Et eksempel kredsløb er vist her:

Induktiv reaktans

Fase Vinkler
Men, vi er nødt til at huske på, at spænding og strøm er ikke i fase her., Som tidligere vist har spændingen et faseforskydning på + 90.i forhold til strømmen. Hvis vi repræsenterer disse fase vinkler af spænding og strøm matematisk i form af komplekse tal, finder vi, at en spole modstand over for nuværende er i en fase vinkel, for:


Aktuelle lag ‘ spænding ved 90° i en spole.matematisk siger vi, at fasevinklen for en induktors modstand mod strøm er 90., hvilket betyder, at en induktors modstand mod strøm er en positiv imaginær mængde., Denne fasevinkel med reaktiv modstand mod strøm bliver kritisk vigtig i kredsløbsanalyse, især for komplekse vekselstrømskredsløb, hvor reaktans og modstand interagerer.
det vil vise sig fordelagtigt at repræsentere enhver komponents modstand mod nuværende med hensyn til komplekse tal snarere end skalære mængder modstand og reaktans.
anmeldelse:
- Induktiv reaktans er modstanden, som en induktor tilbyder vekselstrøm på grund af dens faseforskydede opbevaring og frigivelse af energi i dets magnetfelt., Reaktans symboliseres med stort bogstav “” ” og måles i ohm ligesom modstand (R).
- Induktiv reaktans kan beregnes ved hjælp af denne formel: 2L = 2nfL
- vinkelhastigheden af et vekselstrømskredsløb er en anden måde at udtrykke dens frekvens på i enheder af elektriske radianer pr. Det symboliseres af det små græske bogstav “omega” eller ω.
- Induktiv reaktans øges med stigende frekvens. Med andre ord, jo højere frekvens, jo mere modsætter den vekselstrøm af elektroner.,
relaterede regneark:
- induktorer Arbejdsark
- Induktiv reaktans Arbejdsark