Support Vector Machine nebo SVM, je jedním z nejvíce populární Dohledem Učení algoritmy, který se používá pro Klasifikaci, stejně jako Regresní problémy. Primárně se však používá pro klasifikační problémy ve strojovém učení.
cílem algoritmu SVM je vytvořit nejlepší hranici čáry nebo rozhodnutí, která může oddělit n-dimenzionální prostor do tříd, abychom mohli v budoucnu snadno umístit nový datový bod do správné kategorie., Tato hranice nejlepšího rozhodnutí se nazývá hyperplane.
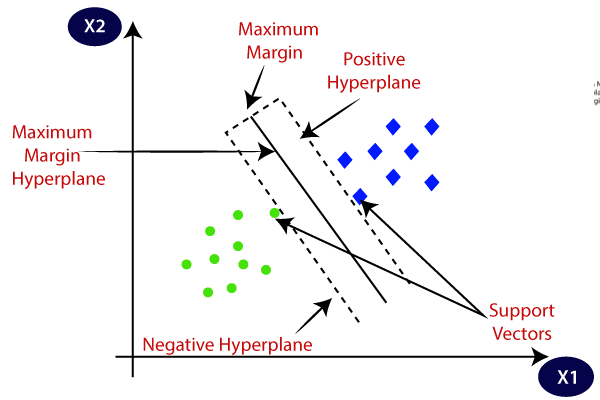
SVM vybírá extrémní body / vektory, které pomáhají při vytváření hyperplane. Tyto extrémní případy se nazývají jako podpůrné vektory, a proto se algoritmus nazývá jako podpůrný vektorový stroj. Zvažte níže uvedené schéma, ve kterém jsou dvě různé kategorie, které jsou klasifikovány pomocí rozhodovací hranice nebo nadrovina:
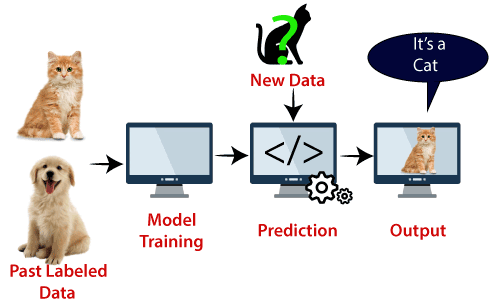
Příklad: SVM lze pochopit na příkladu, který jsme použili v KNN klasifikátor., Předpokládejme, že vidíme podivnou kočku, která má také některé rysy psů, takže pokud chceme model, který dokáže přesně určit, zda se jedná o kočku nebo psa, může být takový model vytvořen pomocí algoritmu SVM. Nejprve budeme trénovat náš model se spoustou obrazů koček a psů, aby se mohl dozvědět o různých vlastnostech koček a psů, a pak to testujeme s tímto podivným stvořením. Takže jak podpůrný vektor vytváří rozhodovací hranici mezi těmito dvěma daty (kočka a pes) a vybírá extrémní případy (podpůrné vektory), uvidí extrémní případ kočky a psa., Na základě podpůrných vektorů ji klasifikuje jako kočku. Zvažte níže uvedený diagram:
algoritmus SVM lze použít pro detekci obličeje,klasifikaci obrazu, kategorizaci textu atd.
Druhy SVM
SVM mohou být dvou typů:
- Lineární SVM: Lineární SVM se používá pro lineárně separabilní data, což znamená, že pokud dataset mohou být klasifikovány do dvou tříd pomocí jedné přímce, pak tyto údaje se označují jako lineárně separabilní data, a třídění se používá tzv. Lineární SVM klasifikátor.,
- nelineární SVM: nelineární SVM se používá pro nelineárně oddělená data, což znamená, že pokud datový soubor nelze klasifikovat pomocí přímky, pak se tato data označují jako nelineární data a použitý klasifikátor se nazývá nelineární SVM klasifikátor.
Nadroviny a Podpůrných Vektorů SVM algoritmus:
Nadroviny: Tam může být více řádků/rozhodnutí hranice oddělit tříd v n-rozměrném prostoru, ale musíme zjistit, to nejlepší rozhodnutí, hranice, která pomáhá klasifikovat datové body. Tato nejlepší hranice je známá jako hyperplane SVM.,
rozměry nadroviny závisí na funkce, které jsou ve dataset, což znamená, že pokud existují 2 funkce (jak je znázorněno na obrázku), potom nadroviny bude přímka. A pokud existují 3 funkce, pak bude hyperplane rovinou 2 dimenzí.
vždy vytváříme hyperplane, která má maximální marži, což znamená maximální vzdálenost mezi datovými body.
Support Vectors:
datové body nebo vektory, které jsou nejblíže k nadrovině a které ovlivňují polohu nadroviny, se označují jako Support Vector., Vzhledem k tomu, že tyto vektory podporují hyperplane, nazývá se tedy podpůrný vektor.
jak funguje SVM?
lineární SVM:
práci algoritmu SVM lze pochopit pomocí příkladu. Předpokládejme, že máme datový soubor, který má dvě značky (zelené a modré) a datový soubor má dvě funkce x1 a x2. Chceme klasifikátor, který může klasifikovat pár (x1, x2) souřadnic v zelené nebo modré barvě. Zvažte níže uvedený obrázek:
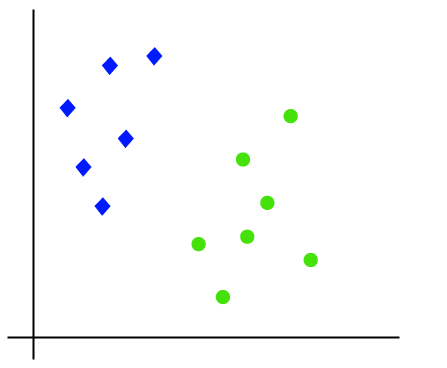
takže je to 2-D prostor, takže pomocí přímky můžeme tyto dvě třídy snadno oddělit., Může však existovat více řádků, které mohou tyto třídy oddělit. Zvažte obrázku níže:
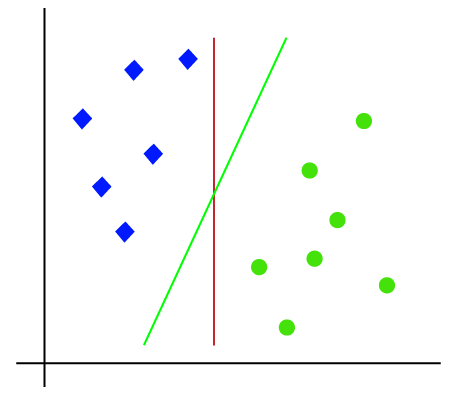
Proto, SVM algoritmus vám pomůže najít nejlepší line nebo rozhodovací hranice; to nejlepší, hranice nebo oblasti, se nazývá nadrovina. SVM algoritmus najde nejbližší bod řádků z obou tříd. Tyto body se nazývají podpůrné vektory. Vzdálenost mezi vektory a nadrovinou se nazývá jako okraj. A cílem SVM je maximalizovat tuto marži. Hyperplane s maximálním okrajem se nazývá optimální hyperplane.,
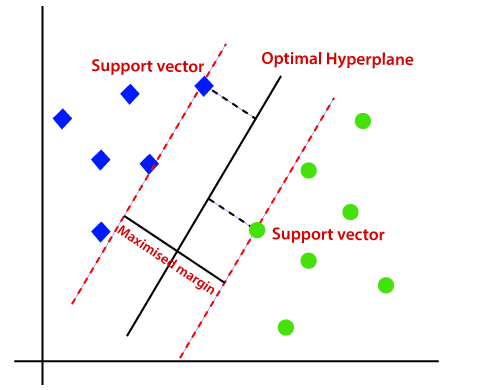
nelineární SVM:
pokud jsou data lineárně uspořádána, můžeme je oddělit pomocí přímky, ale pro nelineární data nemůžeme nakreslit jednu přímku. Zvažte obrázku níže:
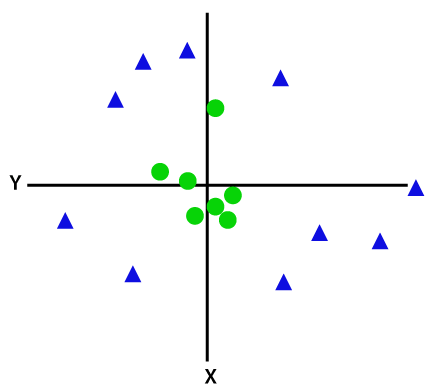
oddělit tyto datové body, musíme přidat ještě jeden rozměr. Pro lineární data jsme použili dva rozměry x a y, takže pro nelineární data přidáme třetí rozměr z., To může být vypočítána jako:
z=x2 +y2
Tím, že přidá třetí rozměr, prostor vzorku bude stát dle obrázku níže:
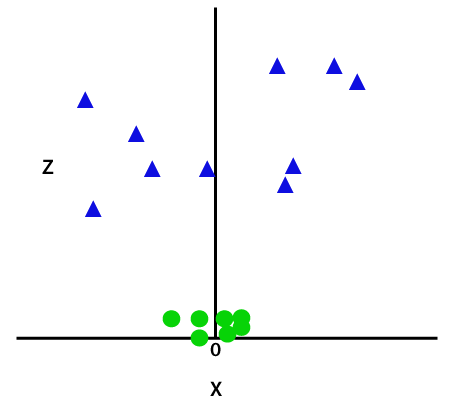
Takže teď, SVM rozdělí soubory dat do tříd následujícím způsobem. Zvažte níže uvedený obrázek:
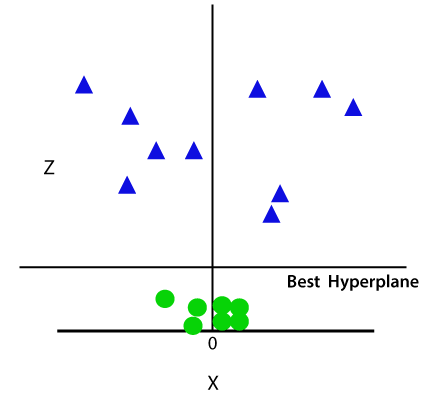
protože jsme v 3D prostoru, proto vypadá jako rovina rovnoběžná s osou x. Pokud jej převedeme do 2D prostoru s z=1, pak se stane jako:
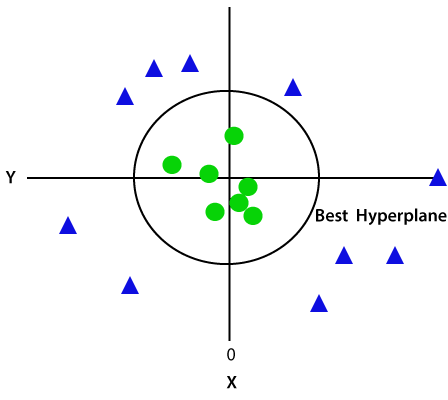
proto získáme obvod poloměru 1 v případě nelineárních dat.,
Python implementace Support Vector Machine
nyní implementujeme algoritmus SVM pomocí Pythonu. Zde použijeme stejný datový soubor user_data, který jsme použili v logistické regresi a klasifikaci KNN.
- krok před zpracováním dat
do kroku před zpracováním dat zůstane kód stejný. Níže je Kód:
po provedení výše uvedeného kódu budeme data předem zpracovávat., Kód dá dataset jako:
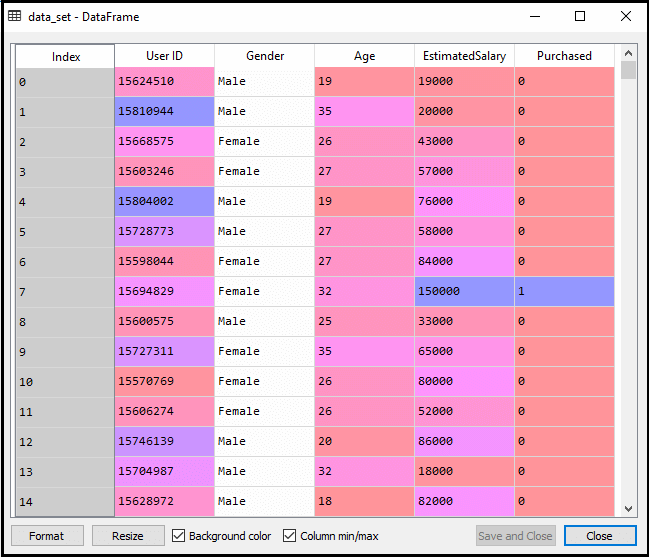
měřítko výstupu pro testovací sada bude:
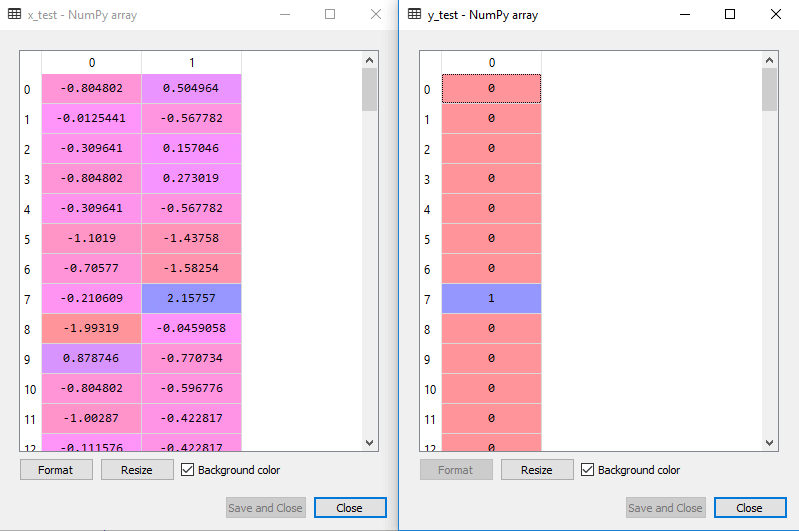
Montáž na SVM klasifikátor k výcviku sada:
tréninkový soubor bude namontováno na SVM klasifikátor. Chcete-li vytvořit klasifikátor SVM, importujeme třídu SVC ze Sklearnu.knihovna svm. Níže je Kód pro něj:
ve výše uvedeném kódu jsme použili kernel= ‚lineární‘ , protože zde vytváříme SVM pro lineárně oddělitelná data. Můžeme ji však změnit pro nelineární data., A pak jsme namontované třídění na školení dataset(x_train, y_train)
Výstup:
model výkon lze měnit změnou hodnoty C(Regularizace faktor), gama, a jádra.
- předpovídající výsledek testu:
nyní předpovídáme výstup pro testovací sadu. Za tímto účelem vytvoříme nový vektor y_pred. Níže je kód pro to:
Po získání y_pred vektor, můžeme porovnat výsledek y_pred a y_test zjistit rozdíl mezi skutečnou hodnotou a předpokládanou hodnotou.,
Výstup: Níže je výstup pro predikci test set:

- Vytváření confusion matrix:
Teď se podíváme na výkon SVM klasifikátor, že to, kolik nesprávné předpovědi jsou zde ve srovnání s Logistické regresní klasifikátor. Chcete-li vytvořit matici zmatku, musíme importovat funkci confusion_matrix knihovny sklearn. Po importu funkce ji nazveme pomocí nové proměnné cm. Funkce má dva parametry, hlavně y_true (skutečné hodnoty) a y_pred (cílená návratnost hodnoty klasifikátorem)., Níže je kód pro to:
Výstup:
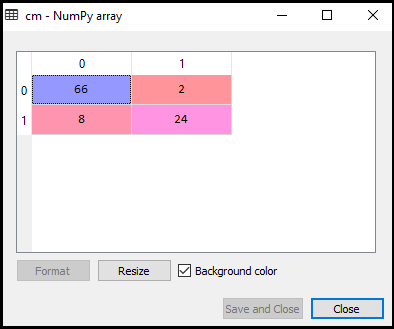
Jak můžeme vidět ve výše výstupního obrázku, tam jsou 66+24= 90 správné předpovědi a 8+2= 10 správných předpovědí. Proto můžeme říci, že náš model SVM se zlepšil ve srovnání s logistickým regresním modelem.,
- Vizualizace školení set výsledek:
Nyní se budeme vizualizovat sadu školení, výsledek, níže je na to kód:
Výstup:
provádění výše uvedený kód, dostaneme na výstupu jako:
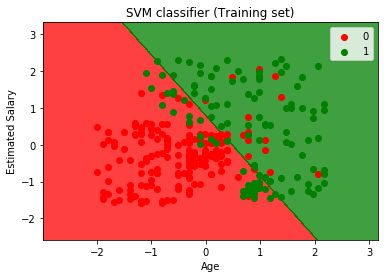
Jak můžeme vidět, výše výstupu se objevují podobné Logistické regrese výstup. Na výstupu jsme dostali přímku jako hyperplane, protože jsme použili lineární jádro v klasifikátoru. A také jsme diskutovali výše, že pro 2D prostor je hyperplane v SVM přímka.,
- Vizualizace test set výsledek:
Výstup:
provádění výše uvedený kód, dostaneme na výstupu jako:
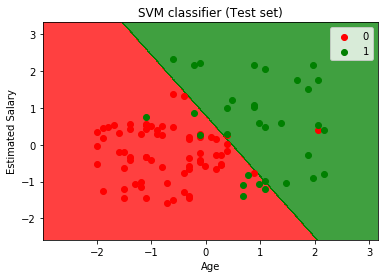
Jak můžeme vidět ve výše výstupního obrázku, SVM klasifikátor má rozdělit uživatele do dvou regionů (Zakoupené nebo Ne koupený). Uživatelé, kteří zakoupili SUV, jsou v červené oblasti s červenými body rozptylu. A uživatelé, kteří si SUV nekoupili, jsou v zelené oblasti se zelenými bodovými body. Nadrovina rozdělila obě třídy na zakoupené a nekupované proměnné.