Odchylka měří, jak daleko sadu dat se šíří ven. Rozptyl nuly znamená, že všechny datové hodnoty jsou identické. Všechny nenulové odchylky jsou pozitivní.

malá odchylka znamená, že datové body mají tendenci být velmi blízko průměru a navzájem., Vysoký rozptyl naznačuje, že datové body jsou velmi rozloženy od průměru a od sebe navzájem. Rozptyl je průměr čtvercových vzdáleností od každého bodu k průměru.

proces hledání rozptylu je velmi podobný nalezení šílené, střední absolutní odchylky.
jediným rozdílem je čtverec vzdáleností.
Proces: (1) Najděte průměr (průměr) sady. (2) odečtěte každou datovou hodnotu od průměru, abyste našli její vzdálenost od průměru. (3) čtverec všechny vzdálenosti. (4) Přidejte všechny čtverce vzdáleností., (4) vydělte počtem kusů dat (pro populační rozptyl).

jedním z problémů s rozptylem je, že nemá stejnou měrnou jednotku jako původní data. Například původní údaje obsahující délky měřené ve stopách mají rozptyl měřený ve čtvercových stopách.,

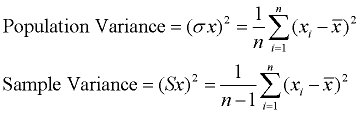Don’t ROUND too soon! When working with the formulas for variance and standard deviation, be careful to avoid rounding too soon., Při ručním výpočtu vždy mějte ve výpočtech více desetinných míst, než se očekává u konečného výsledku. Pokud pracujete s kalkulačkou, noste plnou hodnotu položek kalkulačky, dokud nedosáhnete konečného výsledku.

Směrodatná odchylka ukazuje, jak moc variability (rozptyl, šíření, rozptyl), z mysli existuje., Představuje „typickou“ odchylku od průměru. Je to populární míra variability, protože se vrací k původním měrným jednotkám datové sady.

nízká směrodatná odchylka znamená, že datové body mají tendenci být velmi blízko průměru. Vysoká směrodatná odchylka znamená, že datové body jsou rozloženy na velký rozsah hodnot.
směrodatnou odchylku lze považovat za „standardní“ způsob, jak zjistit, co je normální (typické), co je velmi velké a co je v datové sadě velmi malé.,

směrodatná odchylka je oblíbeným měřítkem variability, protože se vrací k původním měrným jednotkám datové sady. Například původní údaje obsahující délky měřené ve stopách mají směrodatnou odchylku také měřenou ve stopách.,

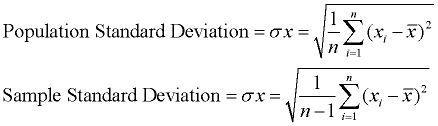Pro výpočet standardní odchylky ručně:
směrodatná odchylka je prostě odmocnina z rozptylu.
tento popis je určen pro výpočet standardní odchylky populace. Pokud je potřeba směrodatná odchylka vzorku, vydělte n-1 místo n., Protože směrodatná odchylka je druhou odmocninou rozptylu, musíme nejprve vypočítat rozptyl.
1. Najděte průměr.
2. Odečtěte průměr od každé datové hodnoty a čtverec každého z těchto rozdílů (čtvercové rozdíly).
3. Najděte průměr čtvercových rozdílů (přidejte je a vydělte počtem datových hodnot). To bude rozptyl.,

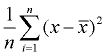rozptyl
4. Vezměte druhou odmocninu. To bude směrodatná odchylka populace. Zaokrouhlete odpověď podle pokynů v problému.

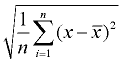směrodatná odchylka

Normální Křivka.

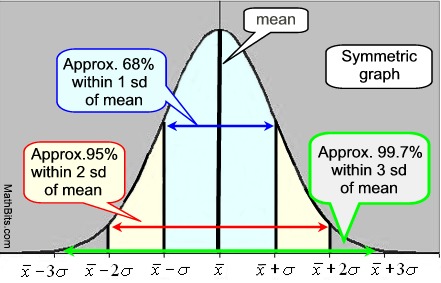
normální křivka je symetrická, zvonek-formoval křivku., Střed grafu je průměr a výška a šířka grafu jsou určeny směrodatnou odchylkou. Když je směrodatná odchylka malá, křivka bude vysoká a úzká v rozpětí. Když je směrodatná odchylka velká, křivka bude krátká a široká. Střední a střední hodnota mají stejnou hodnotu v normální křivce.

Normální Křivka Empirické Pravidlo:
Přibližně …

* 68% údajů leží v jedné směrodatné odchylce průměru.,

* 95% dat leží ve dvou standardních odchylkách průměru.

* 99,7% dat leží ve třech standardních odchylkách průměru.

IQR pro normální křivku je 1.34896 x směrodatná odchylka.