výpočet plochy pod křivkou.
definitivní integrály
při integraci vždy zůstal konstantní termín. Z tohoto důvodu jsou takové integrály známé jako neurčité integrály. S určitými integrály integrujeme funkci mezi 2 body, a tak můžeme najít přesnou hodnotu integrálu a není třeba žádných neznámých konstantních termínů .,

oblast pod křivkou
oblast pod křivkou mezi dvěma body lze nalézt provedením určitého integrálu mezi oběma body.
najít oblast pod křivkou y = f(x) pro x mezi x = a a x = b, integrovat y = f(x) mezi limity a a b.
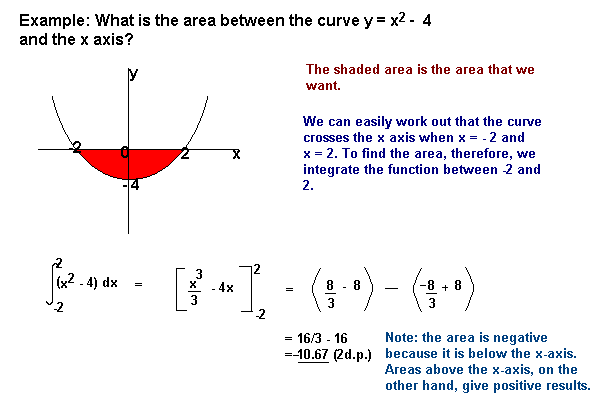
Plochy pod osou x vyjde negativní a oblasti nad osou x bude pozitivní. To znamená, že musíte být opatrní při hledání oblasti, která je částečně nad a částečně pod osou x.,
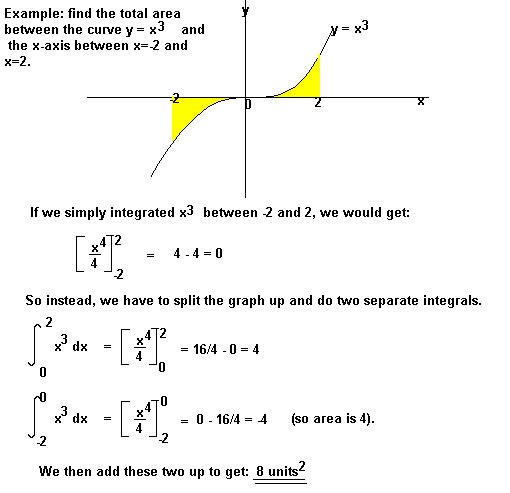
můžete být také požádáni o nalezení oblasti mezi křivkou a osou y. K tomu, integrovat podle y.
Příklad:
Najít oblast ohraničena čarami y = 0, y = 1 a y = x2.